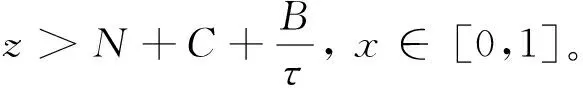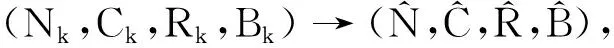一类具有年龄结构的捕食-食饵反应扩散恒化器模型
张 帅,王治国
(陕西师范大学 数学与信息科学学院,陕西 西安 710119)
1 引言与研究模型
近年来, 非均匀恒化器模型的研究受到越来越多的关注。与竞争型非均匀恒化器模型相比, 捕食型非均匀恒化器模型的研究难度大,相关的研究工作目前仍较少。 文献[1-3]研究物种竞争同一资源的恒化器模型, 得到了物种的共存、灭绝等模型。 Nie等[4]讨论了一个竞争者产生毒素抑制另一竞争者的竞争型恒化器模型, 应用度理论和一直持续性理论得到模型解的共存和双稳状态的可能性, 并通过数值模拟的方法验证了理论结果。 类似的一系列研究极大地促进了竞争型恒化器模型的发展。Leung 等[5-6]研究了带有扩散的捕食-食饵模型, 讨论了解的稳定性;文献[7]研究了交叉扩散-捕食食饵模型, 得出了非负平衡解的全局渐近稳定性。 这些研究促进了捕食-食饵反应扩散模型的快速发展, 但是捕食-食饵反应扩散模型的研究并不完善, 需要进一步的研究、发展并完善捕食-食饵反应扩散模型。
本文研究一类带有年龄结构的捕食-食饵反应扩散恒化器模型的动力学行为。 本文的模型来源于2000年Fussmann 等[8]提出的带有年龄结构的捕食食饵模型
(1)
式中:N、C、R、B分别为t时刻营养物浓度、小球藻浓度、可育轮虫浓度以及轮虫浓度;N0、δ、τ、m、α均为正常数;δ代表输出率;τ代表轮虫对藻类的吸收率;m代表轮虫的死亡率;α代表可育轮虫的衰老率。 反应函数f1(N)=b1N/(k1+N),f2(C)=b2C/(k2+C),其中,b1、b2分别是藻类、轮虫的最大生长速率,k1、k2分别表示相应的半饱和常数。 Fussmann等通过实验和数值模拟最终得出捕食者和食饵可能出现循环、平衡、捕食者灭亡或捕食者食饵都灭亡的情况, 但缺乏理论证明验证其结果。 洪等[9]简化了Fussmann的模型, 并研究了模型的渐近稳定性。本文考虑的物种生存与空间有关, 结合Leung等[5]的想法, 在Fussmann模型的基础上引入扩散, 研究具有扩散的捕食-食饵模型
(2)
边界条件为
(3)
初始值条件为
(4)
式中:d>0为扩散系数;γ>0为常数;N0(x)、C0(x)、R0(x)、B0(x)是关于x∈ [0,1] 上的连续函数。结合生物实际,假设
B0(x)≥R0(x),x∈ [0,1]
(H)
系统(2),(3)对应的平衡态方程为
(5)
边界条件为
(6)
由于物种及营养物浓度具有非负性,故只考虑系统(2)~(4)与系统(5)、(6)的非负解。 年龄结构的引入导致守恒定律在系统(2)~(4)中失效,对研究系统(2)~(4)解的性质造成了一定的困难。本文通过应用一致持续性理论, 得到抛物系统(2)~(4)至少存在一个正稳态解;利用局部和全局分歧理论, 分析了系统解与死亡率的依赖关系。
2 解的全局存在性
首先给出系统(2)~(4)解的L∞估计, 从而建立模型解的全局存在性。 假设R0(x)≡0,B0(x)≡0, 则 (R,B)≡(0,0), 于是系统(2)~(4)退化为
(7)
引理1系统(7)的解 (N(x,t),C(x,t)) 是非负的, 有界的, 并且∃α>0, 当t充分大时有
‖N(x,t)+C(x,t)-z(x)‖∞=
O(exp(-αt))
(8)
证明参见文献[10]中引理2.1和文献[11]的引理 3.4.1,类似可证。
引入空间
设μ是特征值问题
(9)
的主特征值。利用文献[12]中引理 2.1以及引理2.2,可得如下结果。
定理1设((N(x,t),C(x,t))∈X1是系统(7)的解,那么以下结论成立:

ⅱ) 如果μ≤0,那么
引理2假设(H)成立,则对任意给定的δ0>0, 当d≥δ0时, 系统(2)~(4)有唯一的解(N,C,R,B), 且存在只依赖于初值(N0(x),C0(x),R0(x),B0(x))的正常数ρi,i=0,1,2,3,使得
证明系统(2)~(4)解的局部存在以及唯一性文献[13]中已证, 故只需证(2)~(4)解的有界性和全局存在性。 为此,令Z(x,t)满足方程
由抛物方程的最大值原理可得0 由强最大值原理[14]可得χ>0,x∈ [0,1],t>0,所以B≥R。注意到 考虑方程式 (10) 显然系统(2)的非负稳态解只有3种情况: ⅰ) 半平凡解E0(z(x),0,0,0); ⅱ) 半平凡解E1(N*,C*,0,0); ⅲ) 正解E2(N,C,R,B)。 引理3当μ<0 时,E0是稳定的;当μ>0 时,E0是不稳定的。其中μ为式(9)的主特征值。 证明考虑系统(2)在E0(z(x),0,0,0)处线性化特征值问题 (11) 且满足 (12) 的主特征值。 证明考虑系统(2)在E1(N*,C*,0,0)处线性化特征值问题 Λ(ψ1,ψ2,ψ3,ψ4)T= (13) 且满足 注意到系统(13)的特征值是由 算子的特征值组成。 (14) 把式(14)的第一,第二个方程相加得到 此时有2种情况: ⅰ) 若ψ1+ψ2≡0, 则ψ2=-ψ1, 于是式(14)可简化为 由于ψ2≢0,故λ是 记系统(2)~(4)的生物可行域为Y={(N,C,R,B)∈C([0,1],R+4):B(x,t)≥R(x,t)}。 令Ψt:Y→Y是系统(2)~(4)的解映射,Y0={(N,C,R,B)∈Y:C≢0,R≢0}, ∂Y=YY0。借助文献[16]引理3讨论系统(2)~(4)的一致持续性。 引理5假设μ>0, 那么E0关于Y0一致弱排斥, 即∃δ1>0,当P0=(N0,C0,R0,B0)∈Y0时,有 (15) 证明因为μ>0, 从而存在充分小的ε1>0,使得μ(ε1)>0, 其中μ(ε1)是下列特征值问题的主特征值: (16) 由函数的连续性知存在常数δ1>0, 当 ‖N(x,t)-z(x)‖∞<δ1 时,有 f1(N)>f1(z)-ε1 (17) 当‖B(x,t)-0‖∞<δ1时,有 (18) 用反证法证明。假设式(15)不成立, 那么∃P0∈Y0,使得 因此,∀δ1>0,∃T1>0,使得 ‖N(x,t)-z(x)‖∞<δ1, ∀t≥T1 (19) ‖B(x,t)-0‖∞<δ1,∀t≥T1 (20) ‖C(x,t)-0‖∞<δ1,∀t≥T1 (21) 根据式(17)~(20)和系统(2)的第二个方程,得到 (22) 因为P0∈Y0, 由强极值原理容易发现C(x,T1)>0。 因此, 存在常数a1,使得 (23) (24) 从式(22)~(24)和比较原理,得到 x∈[0,1],t≥T1 (25) 证明证明类似于引理 5 的证明。 (26) 证明若P0=(N0,C0,R0,B0)∈Y0,由于假设(H) 成立, 类似引理 2可得B(x,t,P0)≥R(x,t,P0)。 由强极值原理以及Hopf边界引理知,∀x∈[0,1],t>0,都有C(x,t,P0)>0,R(x,t,P0)>0,B(x,t,P0)>0,所以∀t>0,有ΨtY0⊆Y0。 (27) 定义连续函数h:Y→[0,∞]形如 ∀φ=(φ1,φ2,φ3,φ4)∈Y 由定理1知,当μ>0系统(2)有半平凡解E1=(N*,C*,0,0), 于是Γ1={(m;N*,C*,0,0):m∈R+} 为系统(2)的半平凡分支。以m作为一个分歧参数, 讨论从半平凡点E1产生的正解分支。 引理7假设 (N,C,R,B)是方程(5)的解, 而且C≢0,R≢0,B≢0, 那么 ⅰ) 0 ⅱ)m 由强极值原理得,在[0,1]上N>0。同理可得C>0,B>0,R>0, 因此(ⅰ)成立。 式中M为常数。 考虑系统(5), 令Q=N*-N,U=C*-C,V=R,G=B, 那么 (28) 其中 显然,F=(F0,F1,F2,F3)对(Q,U,V,G)是连续可微的,F(0,0,0,0)=0, 而且F的Fréchet导数D(Q,U,V,G)F|(0,0,0,0)=0。令 其中M1充分大,使得 f2(C*)-(m*+α)+M1>0 对p>1,令X=(W2,p(0,1))4, 那么X(C1[0,1])4。定义TM1:→R+×X→X如下: 则TM1(m;Q,U,V,G)是X上的紧微分算子。 令 A(m;Q,U,V,G)=(m;Q,U,V,G)- TM1(m;Q,U,V,G) 那么A:R+×X→X是C1光滑的, 并且A(m;Q,U,V,G)=0,N*-z L0(m*;0,0,0,0):=D(Q,U,V,G)A(m*;0,0,0,0) (29) (30) 类似于文献[21]的引理 4.1 的证明,可得结论如下: 引理8方程(30)存在唯一解(Q1,U1)。 引理9问题 (31) 证明由定理2可得结论成立。 (32) Z=R(L0(m*;0,0,0,0))= 且 可证(m*;N*,C*,0,0)是系统(5)、(6)的一个分歧点, 而且在它的邻域内,系统(5)、(6)存在正解分支 Γ={(m(s);N(s),C(s),R(s),B(s)):0 其中 应用Fredholm算子的全局分歧定理(见文献[23]定理 4.3~4.4)把局部分支延伸到全局分支。由T:R+×X→X是C1光滑和紧的, 利用文献[21]定理1.4的证明得Fréchet导数 D(Q,U,V,G)A(m;Q,U,V,G) ∀(m;Q,U,V,G)∈R+×X 是指数为0的Fredholm算子。应用文献[23]的定理4.3,得到集合 {(m;Q,U,V,G)∈R+×X:A(m;Q,U,V,G)=0, (Q,U,V,G)≠(0,0,0,0)} C′={(m;N,C,R,B):N=N*-Q,C=C*-U, R=V,B=G, (m;N,C,R,B)∈C} 那么Γ∈C′。记P={(N,C,R,B)∈(C1[0,1])4:N>0,C>0,R>0,B>0,x∈[0,1]},那么C′∩(R+×P)≠∅。令C*=C′∩(R+×P),C*由分歧点 (m*;N*,C*,0,0) 附近的局部正解分支Γ组成, 即C*⊂(R+×P)在点(m*;N*,C*,0,0) 的小邻域内。 令Γ-={(m(s);N(s),C(s),R(s),B(s)):-δ ⅱ) 不是紧的; ⅲ) 包含点 (m;N*-Q,C*-U,R,B), 其中(Q,U,V,G)≠0,(Q,U,V,G)∈Z。 参见文献[21]定理 1.4 证明,可证ⅰ),ⅲ) 不成立。 由引理7得系统(5)的任意正解 (N,C,R,B) 满足 0 ‖N‖C1, ‖C‖C1, ‖R‖C1, ‖B‖C1≤M。 条件(ⅱ)意味着C*-{(m*;N*,C*,0,0)}⊄R+×P, 故∃ {(m*;N*,C*,0,0)}∩∂(R+×P) (33)3 平衡解的稳定性



4 一致持续性







5 分歧解