基于共享逆近邻与指数核的密度峰聚类算法

高 月,杨小飞,马盈仓,汪义瑞

(1.西安工程大学 理学院,陕西 西安 710048;2.安康学院 数学与统计学院,陕西 安康 725000)

0 引 言

聚类分析是模式识别、图像处理、生物信息分析等领域[1-3]重要的研究分支之一,也是最为常见且具有潜力的发展方向之一。聚类分析是根据某种相似性度量分析数据集,将没有标签的数据划分成若干个不同的簇,使得同一个簇中的样本点彼此相似,不同簇中的样本点彼此不同。常用的聚类方法主要有5种:基于划分的方法[4-5],基于层次的方法[6-8],基于网格的方法[9-10],基于模型的方法[11],基于密度的方法[12-13]。

密度峰聚类算法(clustering by fast search and find of density peaks, DPC)是2014年由Rodriguea[13]提出的，该算法可以自动选取样本的聚类中心点,而且可以处理任意形状的数据。算法选取聚类中心的原则是:具有较高局部密度,且与其他高密度点之间的“距离”较大。尽管DPC算法相比其他聚类算法具有明显优势,但也存在一些缺点。①算法的局部密度定义问题。算法的相似度与密度仅通过欧氏距离与截断距离dc确定,使得算法在高维或多密度数据集中的聚类效果相对较差[14]。②算法的聚类策略问题。算法将样本点划分到距其最近且密度比其大的样本所在的簇,这样的分配策略很容易出现多米诺骨牌效应,即一个样本点分配错误进而导致一连串的样本点分配错误。

对此一些相应的改进算法被提出[15-18]。 KNN-DPC算法[15]是一种基于k个最近邻居的密度峰聚类,算法将k个最近邻居的思想引入DPC算法中构造相似度。样本的近邻点可以更好地反映数据集的局部分布特征,有效提高了DPC算法的聚类效果。谢娟英等[16]提出了一种基于K-近邻的快速密度峰值搜索并高效分配样本的聚类算法,算法通过样本点的K-近邻定义局部密度,并且提出2种基于K-近邻的样本分配策略,由于该算法发现数据集的隐藏信息,从而提高了数据集的聚类效果。NDPC算法[17]基于逆近邻构造局部密度,有效解决了密度不均衡问题。文献[18]提出一种基于共享K-近邻的密度峰算法,算法通过共享K-近邻定义新的相似度与密度,并提出两步分配策略,有效解决了DPC算法中局部密度定义问题和聚类分配策略问题。

目前,大部分密度峰聚类算法在构造样本点的相似度时都忽略了两点之间的共享逆近邻,两点的共享逆近邻能更好表示数据之间的相似性。为了更好地解决上述问题,本文提出一种基于共享逆近邻与指数核的相似度,通过该相似度构造一种新的密度,并通过DPC算法初始聚类后应用到凝集层次聚类(GDL)算法中,形成基于共享逆近邻与指数核的密度峰聚类算法(SRNNEK-DPC)。

1 相关算法

1.1 DPC算法

DPC算法[13]假定每个簇中密度最大的点为聚类中心,并且该点被所在簇中的其他密度较低的点所包围,同时每个簇中的聚类中心点都相距较远。 DPC算法中的相关定义如下:

定义1局部密度 设样本集X={x1,x2,…,xN},DPC算法通过截断距离和样本点之间的欧氏距离计算样本的局部密度ρ。假设样本点xi∈X,则样本点xi的局部密度定义为

(1)

当数据集较小时,DPC算法借助指数核函数定义样本的局部密度

(2)

定义2距离 如果样本点xj的密度ρj高于xi的密度ρi,则距离δi为样本点xi与xj的最小距离。此外,如果xi的密度ρi最大,则δi为xi到其他点的最远距离定义为

(3)

定义3聚类中心 样本的聚类中心点由样本点的局部密度ρ和距离δ共同确定。理想的聚类中心定义为相距较远且密度较高的点,即局部密度ρ和距离δ相对较大。定义如下:

γi=ρiδi

(4)

选取前L个较大的γ值所对应的点为聚类中心点,这里L为最终聚类个数。

1.2 GDL算法

GDL算法[19]是一种简单有效的基于图的凝聚层次聚类算法,用于聚类高维数据。算法首先生成多个初始类簇,然后迭代选择具有最大亲和度的2个类簇进行合并。主要通过平均入度和平均出度的乘积定义簇的相似度度量。平均入度反映样本附近的密度,平均出度刻画样本周围的局部密度。该算法具有性能好,易于实现,计算效率高等优点。

GDL算法中的初始类簇L′=e×L,其中e为要设置的自由参数,L为最终聚类簇数。该算法聚类相似度定义如下:

设样本X={x1,x2,…,xN},构建有向图G=(V,E),其中V是对应于X中样本的顶点集,E是连接顶点的边集。该图与加权邻接矩阵W=[wij]相关联,其中wij是从顶点i到j的边的权重。为了捕获高维空间中的流形结构,该算法使用KNN图,其中权重被定义为

(5)

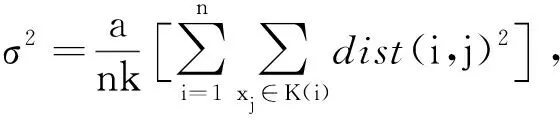
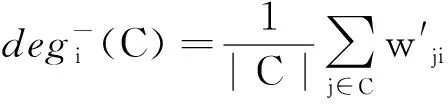
(6)

簇Cb到Ca的相似度定义为

(7)

那么Ca和Cb之间的对称相似度为

ACa,Cb=ACb→Ca+ACa→Cb

(8)

2 SRNNEK-DPC算法

2.1 定义

定义4共享逆近邻[20]设R(i)为样本点xi的逆近邻,R(j)为样本点xj的逆近邻,则样本点xi与xj的共享逆近邻Rs(i,j)定义如下:

Rs(i,j)=R(i)∩R(j)

(9)

定义5相似度 假设样本点xi,xj∈X,则样本点xi与xj之间的相似度S(i,j)定义如下:

S(i,j)=|Rs(i,j)|·

(10)

式中:||表示集合元素的个数;q为样本点xi与xj的共享逆近邻点。

由式(10)可得,当xi、xj与其共享逆近邻点的距离较大或共享逆近邻数较少时,这2个点的相似度较小;当xi、xj与其共享逆近邻点的距离较小或共享逆近邻数较多时,这2个点的相似度较大。说明了该相似度同时涉及到距离信息和局部结构信息,从而能更好地解决密度不均衡问题和高维数据的分布问题。

样本点的逆近邻能更好地反映密度变化[20]。因此,样本点的密度定义为每个点与其逆近邻点的相似度之和。

定义6密度 假设样本点xi∈X,则样本点xi的密度定义如下:

(11)

DPC算法与SRNNEK-DPC算法在人工数据集上的聚类结果如图1所示。从图1(a)可看出，该数据集为多密度人工数据集,由2个稀疏簇和1个密集簇组成。从图1(b)、(c)中可以看出,由于DPC算法的局部密度定义问题导致聚类中心选取错误,在密集簇中有2个聚类中心,而其中1个稀疏簇中没有聚类中心。由于算法的聚类中心选取问题和聚类策略问题进而导致聚类结果不精确。而本文提出的SRNNEK-DPC算法较DPC算法的聚类结果更准确的找出了该数据集中稀疏簇和密集簇的聚类中心,并且将其余样本点准确的划分到簇中。由上可得,本文提出的算法有效改善DPC算法的缺陷并且可以更加准确地对数据进行聚类。

2.2 SRNNEK-DPC算法流程

输入:样本X={x1,x2,…,xN}，初始聚类簇数为L′,最终聚类簇数为L。

输出:聚类结果C={C1,C2,…,CL}。

步骤1 通过式(10)计算每个样本点xi与其逆近邻点的相似度。

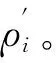
步骤3 通过式(3)计算每个点xi对应的距离δi。

步骤5 首先对得到的γ={γ1,γ2,…,γN}进行降序排序,然后在排序后的列表中选取前L′个样本点作为聚类中心。

步骤10 如果L′>L,转到步骤7,否则,转到步骤11。

步骤11 返回C。

2.3 时间复杂度

SRNNEK-DPC算法的时间复杂度主要由4部分构成:①计算样本点之间的相似度,时间复杂度为O(n2)。②计算样本点的密度,时间复杂度为O(n2)。③生成初始类簇,时间复杂度为O(n)。④生成最终类簇,时间复杂度为O(n3)。综上可得,SRNNEK-DPC算法的整体时间复杂度为O(n3)。

3 实 验

以准确率(accuracy,ACC)[21]和标准化互信息(normalized mutual information,NMI)[22]为评价指标验证SRNNEK-DPC算法的有效性,在真实数据集上进行聚类实验,并与K-means 算法、DPC算法、KNN-DPC算法、CLR算法、GDL算法和NDPC算法进行比较。

实验参数设置如下:对于K-means算法,每个数据集分别做10次实验并取结果的平均值;对于DPC算法,设置p%位置对应的距离为算法的截断距离dc,根据文献[14],设置参数p的取值范围为[1,2,5,10,20,60];对于KNN-DPC算法,参数k的值由k=p×N确定,其中N为数据集中样本点的个数,p的取值范围与DPC算法相同;对于GDL算法,根据文献[19]设置参数;对于SRNNEK-DPC算法,设置近邻参数k为[1,25],初始聚类簇数e的取值范围为{5,10},由于该算法中参数较多,设定构建KNN图的参数k的取值范围为[5,20],参数a为1;对于NDPC算法,根据文献[17],设置参数p的取值范围为{1,3,10}。

本小节选取8个数据分布各不相同的数据集[23-26]对各个算法进行聚类实验。详细信息如表1所示。

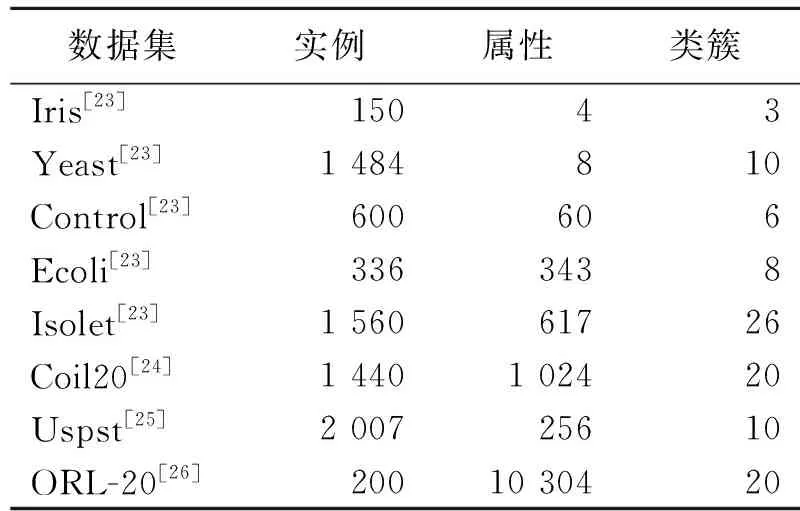
表 1 真实数据集Tab.1 The real datasets

各算法在真实数据集中的聚类结果如表2～3所示,表中加粗数据为该数据集在几个算法中的最优值。由表2可知,除了Iris数据集,在其他数据集中SRNNEK-DPC算法的聚类精度要优于其他算法,而在Iris数据集中,KNN-DPC算法的聚类精度优于SRNNEK-DPC算法,但2个算法的聚类精度相差不大。由表3可知,在 Yeast数据集与Uspst数据集中GDL算法的标准互信息值要高于SRNNEK-DPC算法,而其他数据集中SRNNEK-DPC算法的实验结果都是最优的。综上可得,SRNNEK-DPC算法实验结果在多数情况下优于其他几种对比算法。

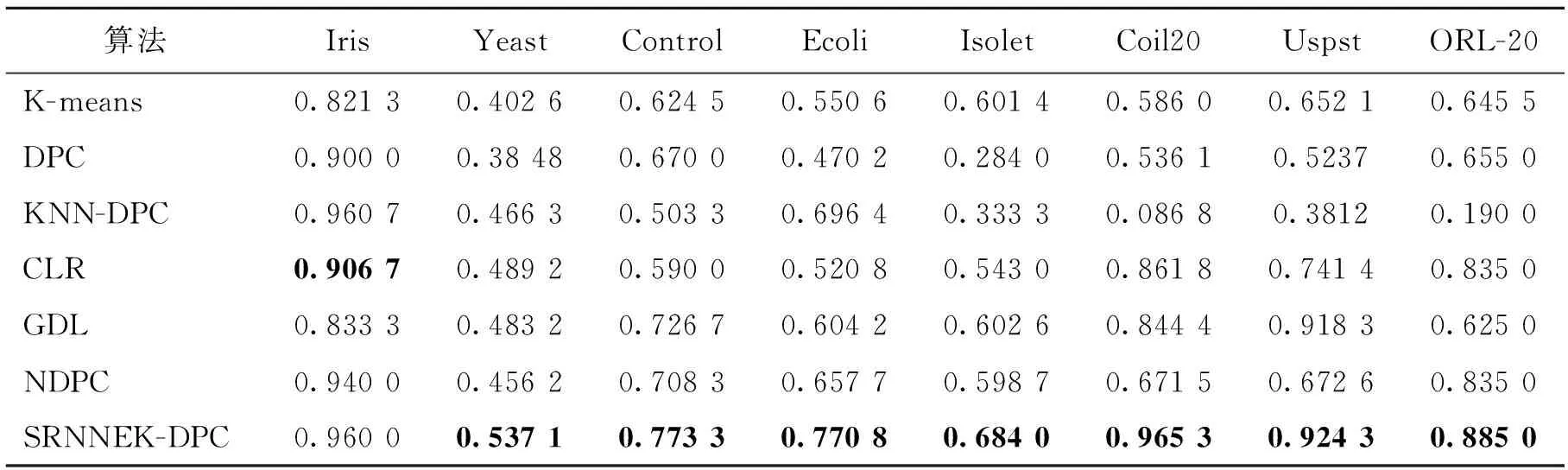
表 2 实验算法在真实数据集中的准确率Tab.2 Accuracy of experimental algorithms in real datasets

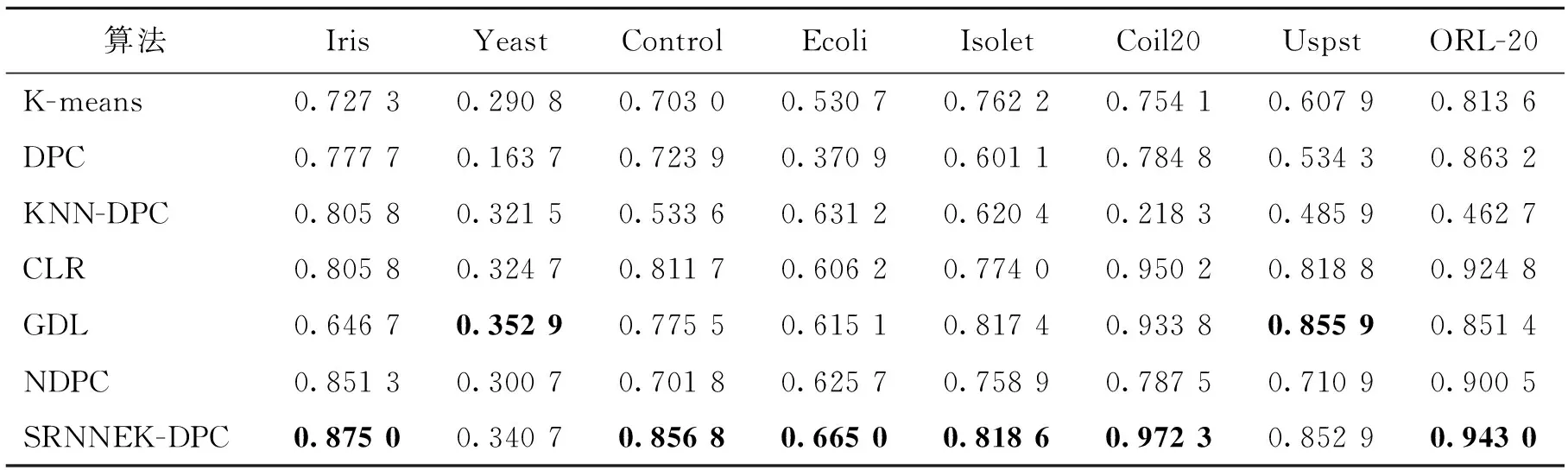
表 3 实验算法在真实数据集中的标准互信息Tab.3 Standard mutual information of experimental algorithms in real datasets

为了更好地说明SRNNEK-DPC算法在高维数据的聚类效果,选取ORL人脸数据集[26]中前20个人的人脸图像进行聚类实验,并将SRNNEK-DPC算法与DPC算法对比。ORL-20数据集总共包含20个人的人脸图像, 每人均有10张不同表情和角度的图像。图2、3分别为DPC算法和SRNNEK-DPC算法在ORL-20人脸数据集上的聚类效果图,同一类簇用相同颜色表示。

对比图2、3可以看出,在ORL-20人脸数据集第3类和第4类(即聚类效果图中第2行的人脸数据) 中,SRNNEK-DPC算法仅有一个错误聚类的人脸,而DPC算法将这2类人脸数据错误聚成了4类;在第5类(第3行左)和第13类(第7行左)中,DPC算法将2类人脸数据错误聚成了一类,而

SRNNEK-DPC算法对这2类的聚类结果完全正确。结合表2可得,SRNNEK-DPC算法的精度要高于DPC算法。因此,本文所提出的算法有效提高了高维数据的聚类精度。

4 结 语

SRNNEK-DPC算法借助逆近邻与指数核定义了一种新的相似度与密度,这种新的密度被应用到DPC算法中可以更准确的发现数据集的聚类中心,有效解决了DPC算法中局部密度定义问题;进而与GDL算法结合有效提高了高维数据的聚类精度。但是,SRNNEK-DPC算法的时间复杂度要高于DPC算法,优化算法的整体复杂度以及与其他聚类算法有效结合有待进一步研究。