深度自编码器的近红外光谱转移研究
刘贞文, 徐玲杰, 陈孝敬
1. 集美大学港口与环境工程学院, 福建 厦门 361021 2. 温州大学机电工程学院, 浙江 温州 325035 3. 温州大学电气与电子工程学院, 浙江 温州 325035
引 言
近红外光谱已广泛应用于各个领域, 是一种快速、 无损、 环保、 经济的实用技术[1]。 然而, 近红外光谱的微弱信号不仅包含化学信息, 还包含各种背景噪声。 因此, 为了从光谱中得到准确的定量分析结果, 一个可靠的多元校正模型是必不可少的。 在实际应用中, 可以使用一种以上的仪器来收集光谱。 将一种仪器(主仪器)的校准模型直接应用于另一种仪器(次仪器)的光谱测量, 会使该模型失效。 而针对新光谱的重新校准是费时的[2-3]。 校准转移的方法可以使用现有的模型来分析在新条件下(新仪器下)获得的新样品, 而不需要重新建立模型, 因此受到许多关注和研究[4]。
模型校准转移主要可以通过三种策略实现: 模型预测值标准化、 模型系数标准化以及光谱标准化(光谱转移)。 简单的单变量斜率和偏差校正(SBC)[5]在两个不同仪器上测量的光谱预测之间建立了线性方程。 通过线性方程的偏置和斜率, 可以对新光谱的预测进行校正。 但只有当仪器变化引起所有样本系统的光谱差异时, SBC才是有效的[6]。 与SBC方法不同, 模型系数的标准化可以应用于不同样本间光谱差异的情况, 但通常这些方法需要大量的光谱样本才能得到满意的参数校正结果。 通过标准化光谱进行模型转移是最常用的模型转移策略, 这类方法通过一个转移矩阵, 将次仪器上测量的样品的光谱转移为相应的主仪器上的光谱, 使其服从于主仪器的样本空间分布。
直接标准化(DS)[7]以及分段直接标准化(PDS)[8]是最具有代表性的标准化光谱方法。 DS直接将在主次仪器上测得的样品的光谱联系起来, 并用变换矩阵来描述这种关系, 主光谱的每个波长与次光谱的所有波长同时相关。 然而, 在PDS中, 频谱相关被限制在一个更小的区域内。 它对一个小窗口区域内的不同仪器测量的光谱之间建立了线性关系, 以实现整体波段的非线性转换。 典型相关分析(CCA)[9]和光谱空间变换(SST)[10]并没有直接对光谱进行校正, 而是从不同光谱中提取出主成分之间的关系。 SST通过对不同仪器上测量的光谱进行比对, 构建数据矩阵, 并通过主成分分析(PCA)来估计光谱转换矩阵。 CCA是一种线性子空间学习方法, 它先用子空间算法降低主光谱的维数, 而后在低子空间中计算了光谱间变换矩阵。
以上提到的算法, 都是基于线性变换实现预测值、 模型系数和光谱的转移。 然而, 在不同仪器上测量的近红外光谱不仅包含遵循朗伯-比尔定律的吸收信号, 还包含与仪器状态, 测量条件, 粒径, 甚至温度和湿度相关的信号[11], 这导致光谱之间非线性的差异。 因此, 仅使用简单的线性模型很难描述在不同仪器上测量的近红外光谱的差别[12]。 本工作使用深度自编码(deep autoencoder, DAE)的方法, 建立了不同仪器之间的非线性映射, 在两个公共数据集上表现优于其他传统线性光谱标准化方法。
1 原理与方法
1.1 深度自编码器神经网络
深度自编码(DAE)是深度神经网络(DNN)的一种特殊类型。 DAE是隐藏层不少于两层的自编码器, 它由编码器和解码器两个部分组成。 作为一种非线性特征提取方法, 编码器建立了自适应多层编码网络, 将高维数据转换为低维码。 解码器使用了与编码器相同网络结构, 可以从代码中重构原始数据。 每一隐藏层的权值代表输入变量的不同重构。 为了恢复输入信号, DAE必须捕获输入最重要的特性。 在编码过程中, 使用反向传播算法最小化原始数据与重构数据之间的差异来训练隐含层的权值。 Ting等[13]利用DAE提取近红外光谱的主要特征, 并将此方法用于近红外光谱的分类。
图1为隐藏层数三层的DAE。 从该图中可以看出, DAE的输入与输出维度相同, 且编码器与解码器具有对称的网络结构。 万能近似定理[14]保证至少有一层隐藏层且隐藏单元足够多的前馈神经网络能以任意精度近似任意函数(在很大范围里), 这是非平凡深度(至少有一层隐藏层)的一个主要优点[15]。 所以, 深度自编码器在给定足够多的隐藏单元的情况下, 能以任意精度近似任何从输入到编码的映射。 这也是深度自编码器优于浅层自编码器之处。
1.2 深度自编码器进行光谱标准化的过程

(1)
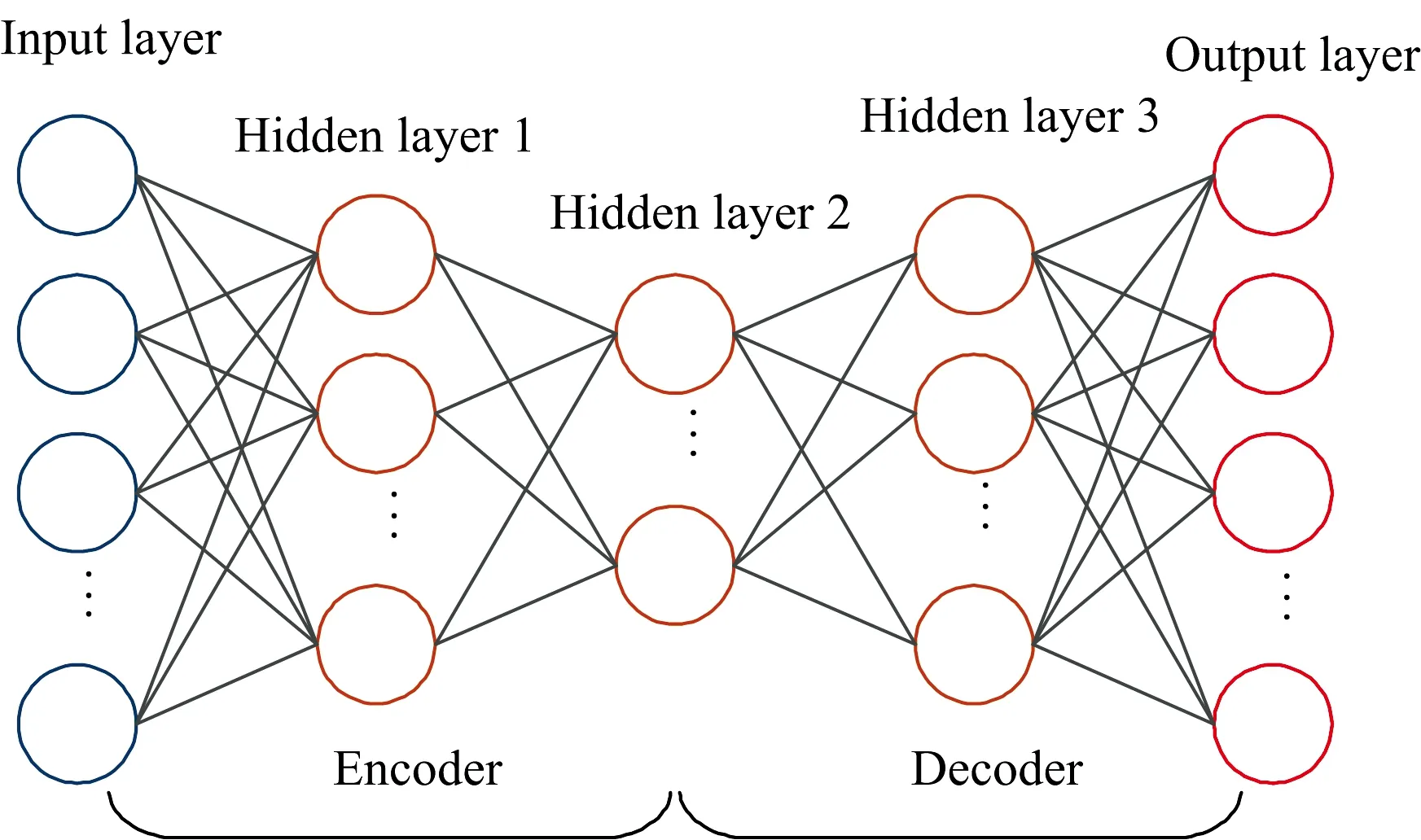
图1 具有三层隐藏层的深度自编码器
所以整体的损失函数为
(2)

θML=argmaxpreconstruct(X2│X1;θ)
(3)
因为样本之间都是独立同分布的, 所以式(3)可以表示为
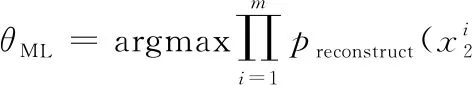
(4)
用log函数将式(4)中的乘积转化为求和的形式, 即对数似然
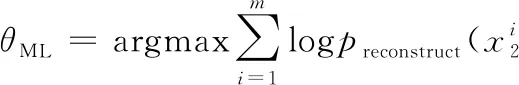
(5)
故可以对DAE的误差函数L加入针对参数θ的惩罚项
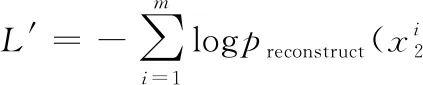
(6)
得到以下惩罚项函数
(7)
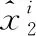
根据式(2)和式(7)整体损失函数可以定义为
(8)
其中λ为惩罚项权重参数。 得到损失函数后, 即可用梯度反向传播方法对网络中的参数θ进行迭代优化, 其中α是学习率。
(9)
2 数据集介绍
利用两个近红外光谱数据集对该方法的有效性进行了验证。 第一个是国际漫反射会议网站发布的药品片剂数据集(http://www.idrc-chambersburg.org/shootout2002.html)。 该数据集包含了655个药物片剂样品的近红外光谱以及每个样本的重量、 硬度和活性药物成分(API)的测定值。 利用美国Foss公司的两台光谱仪, 测定的光谱波长范围为600~1 898 nm, 分辨率为2 nm(纳米)。 该数据集的655个样本被分为校准、 验证和预测集三个部分, 分别包含155, 40和460个样本。 两台仪器得到的光谱样本被用来互相转移, 使用API验证光谱转移后定量校准模型的预测效果。 在计算中, 由于1 794~1 898 nm波段的光谱噪声太大, 无法获得合理的校准结果[16], 因此使用了建议的600~1 792 nm波段的597个变量。 数据集中的可能的不合理谱线: 校准集中的第19, 122, 126和127条, 预测集中的第11, 145, 267, 295, 342, 313, 341和343条谱线被剔除[6], 剩余的数据集中包含642个样本。
第二个数据集是玉米数据集(http://software.eigenvector.com/Data/Corn/index), 包含了m5, mp5, mp6三种仪器上测量的近红外光谱, 以及80个玉米样品的水分、 油脂、 蛋白质和淀粉含量。 每条光谱测量范围为1 100~2 498 nm, 分辨率为 2 nm。 三种仪器测量的光谱被用来互相校正, 用蛋白质含量来验证光谱转移后定量较准模型的预测结果。
在计算之前, 每个数据集都会根据经典的Kennard-Stone(KS)[17]算法被划分为校准集、 验证集和预测集。 药片集的642个样本被分为400个样本的校准建模集, 以及各包含121个样本的验证集和预测集。 玉米集的80样本被分为40, 20, 20的校准建模集、 验证集和预测集。 校准建模集和验证集的光谱样本会被用于建立定量分析的多变量回归模型以及训练用于光谱转移的DAE模型。 预测集的光谱样本用来检验DAE的效果, 同时检验转移后的光谱在原多变量回归模型中的预测结果。
3 结果与讨论
3.1 基于DAE的光谱校正转移
针对药片数据集和玉米数据集, 我们分别设计了两个编码器层数为四层的深度自编码器网络, 结构分别的[597 400 200 100 200 400 597]和[700 350 175 80 175 350 700]。 因此, 输入的仪器一的药片光谱维度, 经过编码器从597逐步变为400, 200, 100, 再经过对称的解码器, 从维度100逐步变为200, 400, 597的输出光谱, 输出的维度为597的光谱即为我们所需的符合仪器二样本分布空间的光谱。 自编码器的损失函数和参数优化方式根据式(8)和式(9)获得。 进行药片数据集光谱转移的自编码器网络结构如图2所示。 玉米数据集的样本也同上进行光谱的转移。
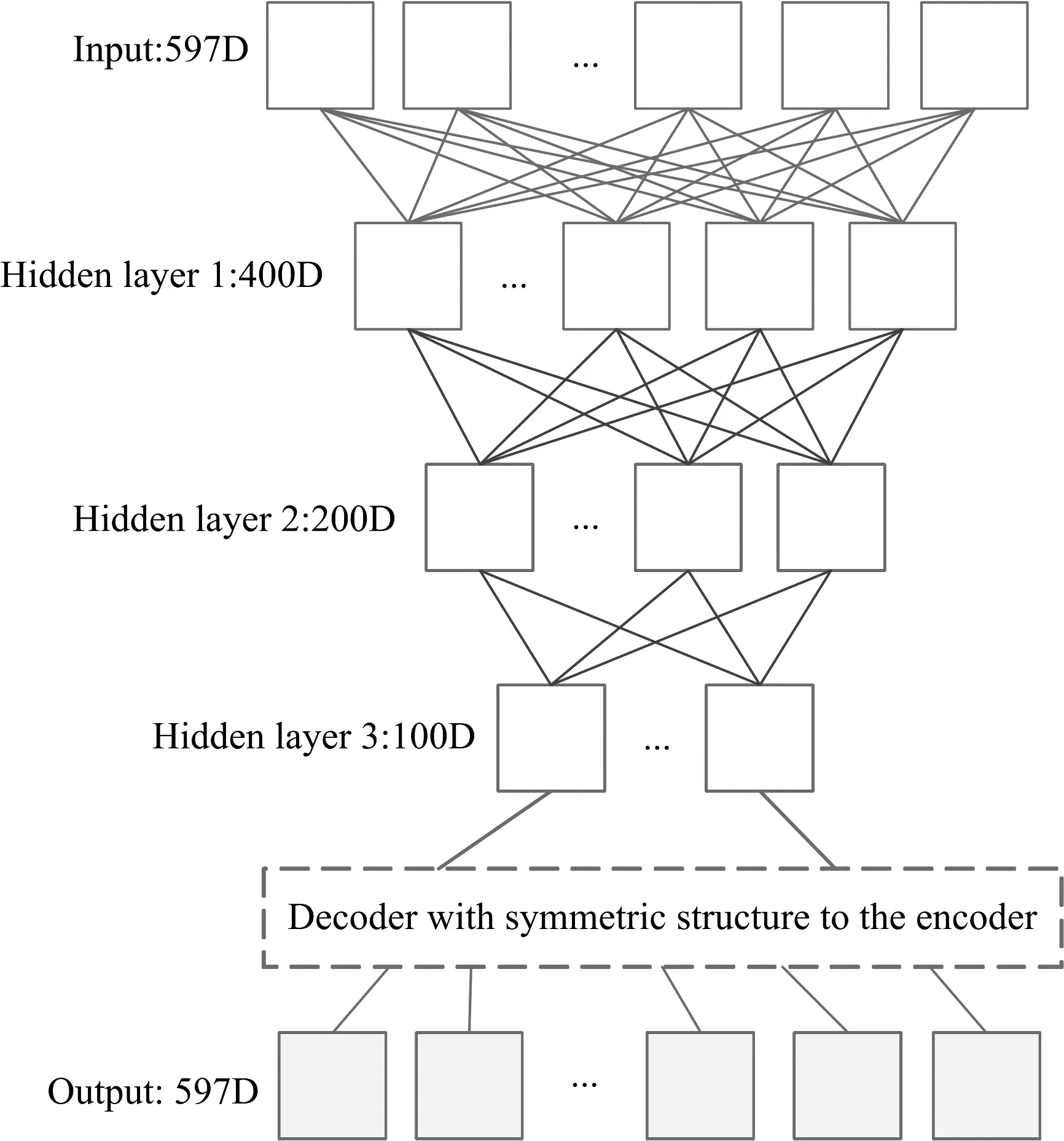
图2 针对药片数据集光谱转移的深度自编码器网络结构
我们使用sigmoid激活函数来限制每层神经元的输出接近于0。 经过多次代码的运行, 确定将式(8)中的惩罚系数λ设置为0.01, 将式(9)中的学习率α设置为0.001, 迭代训练5 000个回合后, 模型收敛, 并达到最佳的转移光谱的效果。
3.2 转移光谱的验证
图3展示了从两个数据集的预测集中随机选取的两台仪器上对应的光谱样本, 对它们进行相互的光谱转移后的可视化结果。 图3(a)是药片数据集的两台仪器上对应的光谱相互转移的结果, 实线是真实的一组具有相同属性值的, 由不同仪器测量出的光谱样本, 虚线是经过3.1中设计的深度自编码器模型转移后的光谱。 从图3(a)中可得, 两条谱线的差异主要集中在波段0~90和500~597 nm, 而在其余波段内, 两条光谱线几乎重合, 说明这两条光谱之间存在着很明显的非线性偏移。 在这主要差异的两个波段中, 虚线与实线重合, 这表明光谱得到了成功的转移。 图3(b)—(d)是玉米样本集的三台光谱仪m5, mp5和mp6上的光谱相互转移的结果。 从三张图可以看出, m5的光谱与mp5和mp6之间偏移较大, 而mp5与mp6光谱偏移小。 图中虚实线吻合, 说明深度自编码器能够有效地对三台仪器得出玉米光谱样本进行两两之间的转移。
3.3 多变量校准模型验证
进行光谱转移是为了将偏移的光谱进行转移后, 直接应用于已建立的多变量校准模型中, 来获得有效的定性定量分析结果。 因此, 为了进一步研究本方法的有效性, 将本方法与经典的线性转移方法PDS和SST算法中得到的转移光谱分别作为测试样本输入已建立的多变量校准模型, 通过比较多变量模型输出的均方根误差(RMSEP)来验证转移的效果。 多变量校准模型通过经典的偏最小二乘法(PLS)算法建立[18]。 通过7次交叉验证, 确定了PLS模型中潜在变量(nLV)的最优数量。 如表1和表2所示, 显然, 当用一台仪器的校准集光谱建立的模型直接预测另一台仪器的光谱, 效果很差。 但当三种方法得到的转移光谱被预测时, RMSEP显著降低。 通过对三种方法的比较, 本方法得到的转移光谱在原校准模型中的表现略优于常用的SST和PDS方法。 不管是哪两台光谱仪之间的相互转移, 均得到了类似的结果。

图3 两个数据集的不同仪器上的光谱相互转移的结果, (a)中的A1和A2代表药片数据集两台光谱仪上测出的光谱
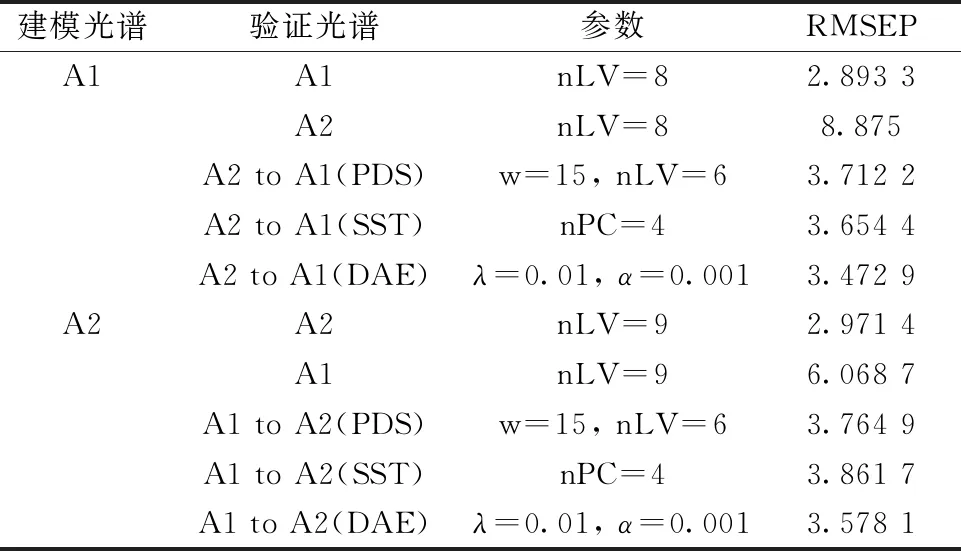
表1 药片数据集进行光谱转移后, 转移光谱在多变量校准模型中的RMSEP
注: nLV: 偏最小二乘法(PLS)的潜变量个数; w: PDS中选用的窗口尺寸; nPC: SST算法中选取的主成分个数
Note: nLV: Number of latent variables in PLS; w: Window size used in PDS; nPC: Number of principal components in SST
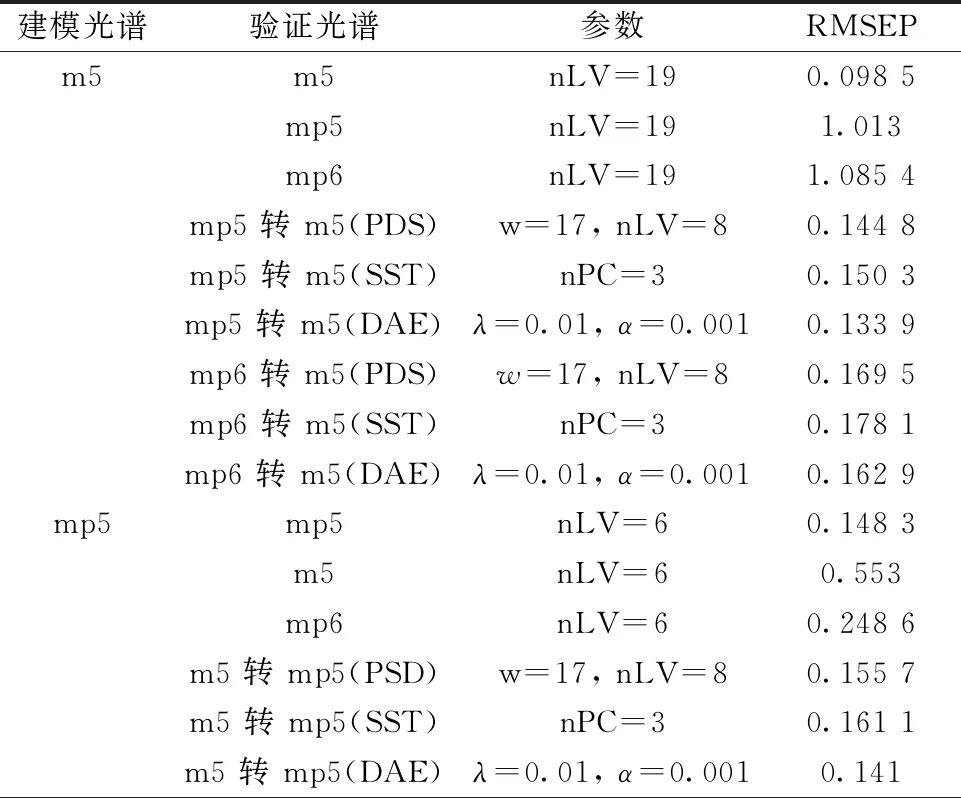
表2 玉米数据集进行光谱转移后, 转移光谱在多变量校准模型性中的RMSEP
续表2

mp6 转 mp5(PSD)w=17, nLV=80.15mp6 转 mp5(SST)nPC=30.159 8mp6 转 mp5(DAE)λ=0.01, α=0.0010.146 6mp6mp6nLV=90.155 2m5nLV=90.677 9mp6nLV=90.192 2m5 转 mp6(PSD)w=17, nLV=80.225 1m5 转 mp6(SST)nPC=30.231 9m5 转 mp6(DAE)λ=0.01, α=0.0010.201 3mp5 转 mp6(PSD)w=17, nLV=80.169 7mp5 转 mp6(SST)nPC=30.179 5mp5 转 mp6(DAE)λ=0.01, α=0.0010.162 3
注: nLV: 偏最小二乘法(PLS)的潜变量个数; w: PDS中选用的窗口尺寸; nPC: SST算法中选取的主成分个数
Note: nLV: Number of latent variables in PLS; w: Window size used in PDS; nPC: Number of principal components in SST
4 结 论
研究了深度自编码在近红外光谱转移中的应用, 探索了一种非线性的光谱转移方法。 通过数理统计的相关知识, 设计了符合光谱转移需求的误差函数。 同时, 针对药片数据集和玉米数据集, 给出了详细网络结构和模型参数。 将预测集样本输入训练好的DAE转移模型, 可以发现转移后的光谱与相应的目标光谱谱线基本重合, 说明本转移模型的有效性。 最后, 为了进一步验证本方法的优越性, 将本方法与SST和PDS方法进行比较。 将这三种算法得到的转移光谱分别作为测试样本, 输入已建立的偏最小二乘(PLS)多变量校准模型, 通过比较RMSEP, 可以发现本方法在多变量校准模型中的预测结果的均方根误差均小于SST和PDS, 平均提高了5.7%和10.1%, 进一步证明了本方法高效和实用的优点。

