基于参考温度的多目标极小值优化原理的多光谱真温反演
张福才, 刘允刚, 孙晓刚
1. 陕西科技大学电气与控制工程学院, 陕西 西安 710021 2. 哈尔滨工业大学仪器科学与工程学院, 黑龙江 哈尔滨 150001
引 言
近些年来, 多光谱光学高温计已经成为高温辐射领域中重要的测量工具[1]。 如何准确可靠地求解出光谱发射率仍然是多光谱测温核心问题, 关于光谱发射率的求解主要以下三种方案: 波长假设模型, 采用光谱发射率与波长之间建立模型来实现真温和光谱发射率反演的方法是目前国内外最常用的方法, 1976年, Svet将光谱发射率和波长之间建立数学模型, 采用含有波长的多项式近似代替未知的光谱发射率, 当方程组处于超定或正定状态时, 可以实现对方程组的求解, 此种方案可以反演出真温和光谱发射率[2]。 经过几十年的发展, 2013年, Rodiet等采用最小二乘法对多光谱辐射温度测量法中的波长的选取进行了优化, 实验中波长采用近红外波段, 波长范围为1.5~5.5 μm, 实现了573~673 K温度的测量[3]。 2015年, 邵艳明等对炼钢过程进行了深入研究, 采用最小二乘法, 利用光谱仪测量得到的光谱信息对转炉炉口火焰温度进行了测量与分析[4]。 同一年, Zhang采用维恩公式代替普朗克公式, 假设某一温度下光谱发射率与波长之间存在线性或非线性关系, 提出光谱识别法的多光谱真温反演算法, 实现了中红外波段真温的反演[5]。 2018年, 杨艺帆等针对辐射测温中未知数大于方程个数的这一客观事实, 假设测量对象的光谱发射率具有缓变的特性, 因此相邻波长处的光谱发射率近似相等, 从而减少了未知数的个数, 实现了真温和光谱发射率的反演[6]。 这类模型真温反演的结果与光谱发射率假设模型关系密切, 而假设模型又有多种类型, 如何选择一种假设模型更为恰当缺乏足够的理论依据, 如果光谱发射率的假设模型选取不合理, 将可能导致较大的真温反演误差。 另外是神经网络假设模型, 1998年, 孙晓刚等首次将神经网络应用于多光谱真温反演的过程中, 结果表明, 大多数情况下, 神经网络法无需建立光谱发射率与波长之间的关系, 是一种有效的多光谱真温反演方法[7]。 2001年, 孙晓刚等先后利用BP神经网络算法和RBF神经网络算法对多光谱测温数据进行了处理, 提出了一种新的多光谱温度测量数据处理的思路, 全面将神经网络算法引入到了多光谱温度测量领域, 得到了良好的测量效果[7]。 这类模型神经网络的多光谱真温反演方法是一种重要的真温反演方法, 但这种方法的Matlab反演程序最为复杂, 而且神经网络都需要事先进行学习, 学习的过程不但需要大量正确、 可靠的数据而且学习本身就需要花费大量的时间, 因此这种方法真温反演的速度也最慢。 有报道真温假设模型于2001年孙晓刚假设光谱发射率与真温之间在一定温度范围内存在某种线性函数关系, 在此模型基础上, 初步提出了二次测量法的理论模型, 完成了相关理论的仿真实验[8]。 2003年后, 孙晓刚完善了光谱发射率和真温的假设模型, 通过迭代的方法可以求解出真温和光谱发射率[9]。 2017年, Liang针对二次测量法反演速度较慢的问题, 增加了发射率模型的非线性约束条件, 提出了一种基于模型约束条件的二次测量法, 这种模型约束条件的二次测量法速度最高提高了43.45%[10]。 这类模型将光谱发射率与真温之间建立模型来实现真温和光谱发射率反演的这种方法是一种独特的真温反演方法, 其真温反演精度较高且具有较好的鲁棒性; 由于采用了迭代的求解方式, 其真温的反演速度并不高, 因此, 如何提高真温和光谱发射率的反演速度以更好地满足实际需要是这种方法亟待解决的问题之一。
在实际的辐射测温过程中, 当一个发射率随波长变化规律是已知的, 采用多光谱测温得到的测温数据相对是合理可靠的, 然而, 绝大多数情况二者之间的关系是不明确的, 甚至是没有任何规律的, 因而会对测量结果的准确性造成较大的影响, 上述多光谱测量方法还是存在一定局限性的。 本研究提出一种基于定点黑体炉参考温度的多目标极小值优化原理的多光谱真温反演方法, 不再考虑光谱发射率与波长、 光谱发射率与真温之间的关系, 也不需要预先建立光谱发射率与波长、 光谱发射率与真温之间的数学模型, 是一种可行的多波长高温计的数据处理方法。
1 基于参考温度的多目标函数极值真温反演原理
从多光谱高温计的测量理论可知, 对于参考黑体在参考温度T的输出电压Vi可表示为
(1)
式(1)中,Aλi是只与波长有关的仪器常数, 它与该波长下探测器的光谱响应率、 光学元件透过率、 几何尺寸及第一辐射常量有关, 称为检定常数, 通过标定可以确定。ελi是温度T时的目标光谱发射率,λi是相应通道的波长,C2是第二辐射常数。 在定点黑体参考温度Trb下, 第i个通道的输出的电压Vλib为
(2)
式(2)中,ελib黑体炉在参考温度Trb=2 252 K时的光谱发射率, 实际计算中取ελib=0.99。 将式(1)和式(2)相除, 得
(3)
应用式(3), 对于n个通道的多光谱测温系统, 可以得到n个测量方程的同时也得到n+1未知数(n个ελi和一个T)。 从理论上讲, 对应无穷多个解, 因此, 必须找到一种方法解决这个问题。 以往的研究方法主要是假设ελi和λi存在某种数学关系, 用含有λi(λi的值一般由通道的滤波片决定, 故为已知量)的表达式代替ελi, 使方程的未知数降为n个后得以求解。 但这种假设关系一旦不存在将对测量结果带来较大的误差。 基于这种原因, 寻找一种合适的不依赖于光谱发射率和波长之间关系假设且具有通用性的数据方法变得日益迫切。
由式(3), 第i个测量通道表示的真温为Ti为
(4)
式(4)中,ελib黑体炉在参考温度时的光谱发射率, 实际计算中取ελib=0.99,ελi是温度T时的目标光谱发射率, λi是相应通道的波长,C2是第二辐射常数,Vλib为第i个通道的输出的电压,Vλi对于待测目标温度为T的输出电压, 通过式(4), 可以被测目标的真温。
1.1 多目标函数
对于含有烟黑、 炭粒或固体颗粒(Al2O3)的火焰, 其辐射光谱主要位于可见光和近红外波段的连续光谱, 每一个光谱通道都可以利用式(4)表示真温。 其中, 光谱发射率是未知数, 由辐射测温的基本可知, 光谱发射率随着波长的变化具有渐变的特征, 相邻两个通道表示的真温差不会相差很大, 因此, 取相邻两个通道表示的真温差最小构成一个目标函数, 即式(5)
F1=min(Tz1-Tz2)
F2=min(Tz3-Tz4)
F3=min(Tz5-Tz6)
F4=min(Tz7-Tz8)
(5)
由辐射测温的基本理论常识可知, 对于同一点、 同一时刻的测量, 真温具有唯一性, 由不同通道表示的真温分别为Tzi和Tz(i+1), 由于测量中随机误差的存在, 造成Tzi≠Tz(i+1), 由于误差的基本可知, 由不同通道表示的真温标准差越小表示测量的可靠性就越大, 测量精度也相对较高, 另外, 由于测量真温是待求的未知量, 因此这里采用贝塞尔(Bessel)公式表示的标准差的平方最小作为一个目标函数, 即
(6)
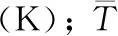
式(5)和式(6)构成了五个目标函数, 由约束优化理论可知, 很难求得真温一个T使五个目标函数同时达到极小值, 因此, 只能将满足五个目标函数的近似解或弱有效解时的T视为被测目标的真温。
1.2 非线性多变量等式约束条件
为了构造非线性多变量等式约束条件, 首先对式(4)的N个光谱通道相加取平均值后再减去式(4)中的第一个通道方程并整理, 得
(7)
通过减法操作, 消去了真温Ti, 由式(7)构成了一个等式方程, 其余的变量如波长λi和亮度温度Ti都是已知量。
1.3 线性多变量不等式约束条件
由辐射测温的基本理论可知光谱发射率的变化范围都在0和1之间, 另外, 根据相关文献, 相邻通道的光谱发射率满足
(8)
式(8)限定了式(7)中非线性多变量等式约束条件变化范围, 减少了冗余数据而且提高了算法的反演速度。 求得的真温Tz并不是约束条件解的交集而是近似有效解或弱有效解, 将这个温度Tz视为被测目标的真温, 这一点与二次测量法的原理相同。 另外, 当多目标函数数量和形式的不同时, 也会对结果产生一定的影响。
2 基于参考温度的多目标函数极值真温反演方法的求解
通过上述原理分析可知, 建立了基于参考温度的多目标函数极值真温反演方法的多目标函数和约束条件。 这种结构与多目标优化结构近似, 多目标优化结构基本的形式为
V-min{f1(X),f2(X), …,fp(X)},X∈Rn
(9)
式(9)中,f1(X),f2(X), …,fp(X)为目标函数表达式,Rn为一个向量,X为自变量,gj(X)≤0和hk(X)=0为不等式和等式约束条件。 因此, 可以使用Matlab工具箱中的中的fgoalattain函数实现多目标函数的求解, 在求解目标函数极值的过程中实现真温和光谱发射率的反演。
3 实验验证
调节黑体炉到某一固定温度, 待其稳定后, 使用单波长高温计测量得到黑体炉的温度为2 252.0 K, 表1为在定点黑体参考温度Trb=2 252.0 K处多光谱高温计有效波长及在参考温度处的电压信号输出, 对于黑体炉而言, 黑体参考温度与亮度温度相等, 对于一般待测目标而言, 其真温都大于亮度温度, 表2为实际测量时各个测量通道的电压, 是本计算的原始数据[12]。

表1 参考温度下的各个测量通道的电压

表2 实际测量时各个测量通道的电压
在黑体炉和微型光谱仪之间分别插入已知光谱特性的JB9, QB18和LB6三种型号的衰减片模拟真实辐射目标, 由多光谱高温计采集的多光谱电压数据通过USB接口传送至计算机。 分别利用二次测量法(second measurement method, SMM)和基于参考温度的多目标极小值优化原理的多光谱真温反演方法(true temperature inversion method for minimum of multi-objective function based on reference temperature, IMR)反演真温并记录了反演时间, 如表3所示; 反演的光谱发射率如表4所示。

表3 真温反演结果
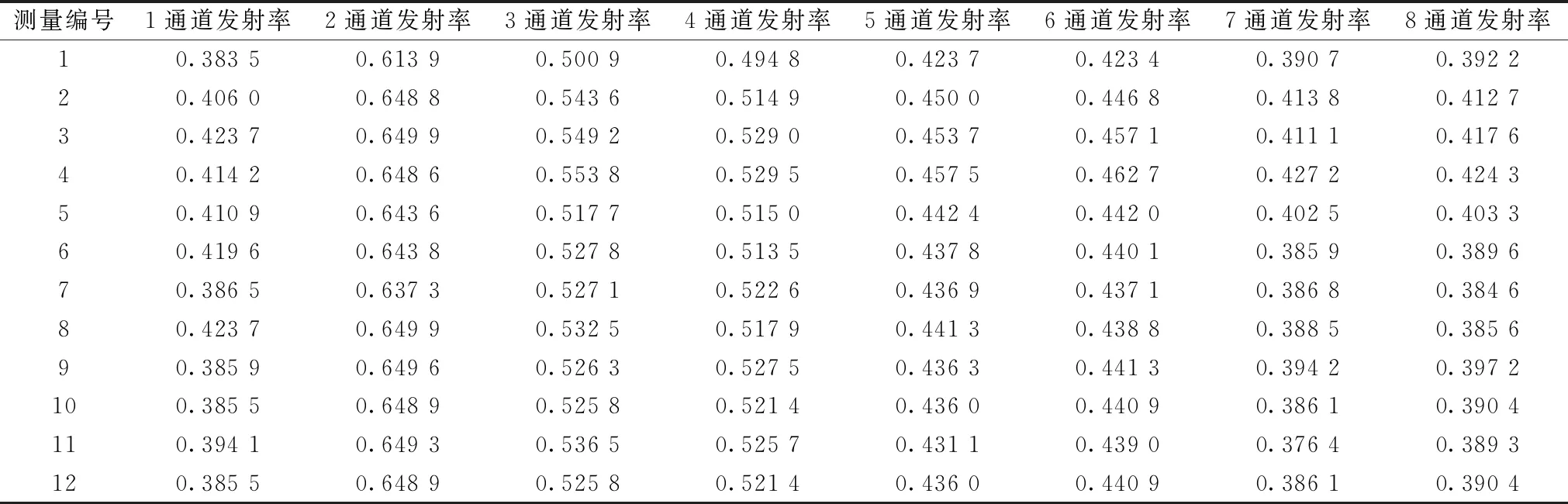
表4 光谱发射率反演结果

图1 光谱发射率随波长的变化曲线
由表3中两种方法反演的结果的对比可知, 两种方法的求解结果基本相同, 都在理论值约2 490.0 K; 在反演时间上, 二次测量法的反演时间都在60 s左右, 而基于参考温度的多目标极小值优化原理的多光谱真温反演方法的反演时间都小于3 s, 反演时间提高的比例均超过95%。
图1为根据光谱发射率绘制的光谱发射率随波长变化的曲线图, 从图中可以看出, 虽然反演的真温值不同, 但每一个真温下光谱发射率随波长先增加后减小的趋势基本相同。
4 结 论
提出了一种基于参考温度的多目标极小值优化原理的多光谱真温反演方法, 可以得到以下结论: (1) 该方法无需对光谱发射率与波长之间的函数关系、 光谱发射率与温度之间的函数关系不做任何限制, 理论上简化了真温反演的原理; (2) 火箭发动机尾焰理论真温约为2 490.0 K, 研究中提出了一种基于参考温度的多目标极小值优化原理的多光谱真温反演方法反演的真温与理论值之差都在±20 K以内, 在相同条件下, 神经网络法和镜像延拓法的真温反演误差在±100 K以内, 本研究提出的反演方法在精度上有了较大的提高; (3) 在反演时间上, 与二次测量法相比, 基于参考温度的多目标极小值优化原理的多光谱真温反演方法的反演时间都小于3 s, 反演速度提高的比例都在95%以上。
本研究提出的基于定点黑体炉参考温度的多目标极小值优化原理的多光谱真温反演方法是一种可行的真温反演的方法, 采用优化思想的真温反演方法很可能成为多光谱真温反演研究的新方向。

