探寻本源 把握本质 回归本真

丁琳

[摘要]数学概念教学应尝试同化学习方式，利用新旧知识的联系进行教学活动的设计，从一位小数和分数的理解引入小数意义的概念，探寻小数是十进分数的本源;借助学生熟悉的长度、质量、容量单位等帮助学生理解小数产生的起源;利用正方形、正方体逐步抽象形成小数的概念，从而完善概念，感悟数学思维。

[关键词]认知同化理论;小数;意义

[中图分类号]

G623.5

[文献标识码]A

[文章编号] 1007-9068（ 2020）20-0063-03

一直以来，数学概念的学习是学生数学学习的难点。根据奥苏贝尔的认知同化理论的观点，新知识的学习必须以已有的认知结构为基础，借助于概括具体事物的共同属性，并将新概念纳入到已有的概念体系之中，并逐步加以“固定”的一种动态过程。奥苏贝尔强调，学生已知内容是影响学生学习的最重要因素，新旧知识之间必须经历同化。因此，概念的学习主要是学生对经验的概括和加强新旧知识之间的联系。因此，这一学习方式需要基于对新知与旧知、新知与已有认知结构的关系进行分析。本文以苏教版教材五年级上册“小数的意义”教学为例，阐述如何把握意义联结，促进学生开展数学概念的深度学习。

一、立足学情，逐步丰富概念

一位小数是学生在三年级已经学习、认识过的，学生通过熟悉的“元、角、分”了解了一位小数和十分之几的关系。基于此，教师借助学生的已有经验，在课始开门见山地提问：“利用以前学过的知识，还可以怎么表示1分米？”这样的问题能帮助学生在认知结构中找到同化新知识的概念，便于学生找到新旧知识之间的相同点。教师继续追问：“0.1米、0.3米、0.7米有什么共同点？”学生在比较中进一步明确了一位小数的意义，丰富了小数概念的内涵。

【教学片段1】创设情境，回顾概念。

师：动物奥运会开幕了，青蛙跳远比赛中谁跳得最远？要想比较精确地记录它们的跳远成绩，怎么办？

生1：3号青蛙跳得最远。要想准确知道成绩，必须要用有刻度的尺子去量。

师：现在谁来说说3只青蛙的跳远成绩是多少？

生2：1分米、3分米、7分米。

师：说说你是怎么想的。

生2：把1米平均分成10份，其中l份表示1分米。

师：用以前学过的知识，还可以怎么表示1号青蛙的成绩？

生3：1/10米、0.1米。

师：0.1米表示什么含义？

生3：0.1米表示1分米，而1分米是1米的1/10，即1/10米。

师：3分米、7分米又可以怎么表示呢？

生4：把1米平均分成10份，3分米可以用3/10米或者0.3米表示，7分米可以用7/10米或者0.7米表示。

师：我们一起来读一读这三个小数，边读边观察它们有什么共同点。

生5：都是零点几。

生6：小数部分都只有一位。

师：我们把这样的小数叫作一位小数。这些分数有什么共同点？

生7：分母都是10的分数。

师：十分之几可以写成一位小数，一位小数也就表示十分之几。

教学中，教师给学生创设了熟悉的动物奥运会和青蛙跳远的情境，激发学生的参与热情，促进学生主动思考。在回顾旧知的过程中，结合“1分米”“3分米”“7分米”，通过适当地扶和放，强化学生对一位小数的共同特点的认识。通过3只青蛙的非线性素材的呈现，学生容易沉浸在情境中，找到小数的知识起点，初步感受小数与分数之间的联系，感悟整数与小数之间的十进制关系。

二、注重迁移，建构小数概念

借助“动物奥运会”的情境和实际产生的问题，学生能比较容易地从一位小数的回顾迁移到两位小数的探究过程，学习兴趣也得到了激发。通过把1米平均分成10份得到一位小数，学生可以简单地联想到不能用整倍数表示时，可以继续把1分米平均分成10份得到1厘米。在平均分的过程中，学生既可以感悟两位小数产生的必然和必要，又可以理解小数的本质。课堂上，通过提问怎么想到把“1/100米”写成“0.01米”的形式，使学生初步感悟平均分得越多越精确，引发学生思考小数产生的价值。

教师在学生经历了一位小数的学习回顾、两位小数的自主探究之后，让学生再去自主探究三位小数、四位小数，学生通过“发现一猜想一验证”的过程，进一步明确了小数的意义，感受产生三位小数、四位小数等的必要性和科学性，进一步把握了小数的概念内涵。

【教学片段2】借助生活模型，理解概念。

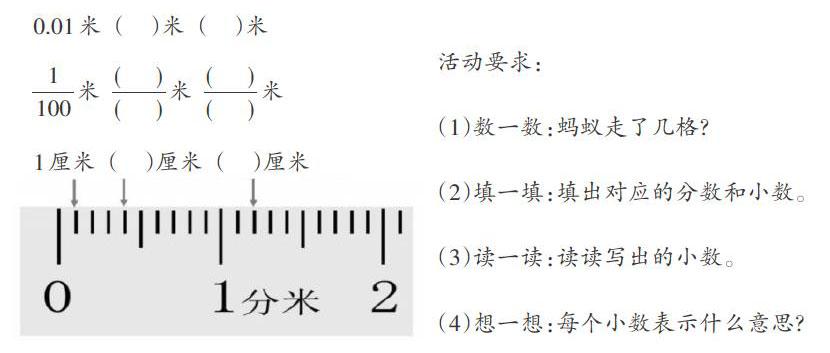
师：看完青蛙比赛，我们一起去看看蚂蚁竞走比赛。蚂蚁现在走了多远？能精准知道它们的成绩吗？

生1：先把1米平均分成100份。

师：我们放大看，第一只蚂蚁刚好走了——

生2：1厘米。

师：想一想，1厘米是几分之几米呢？

生3：1米是100厘米，1厘米是1米的百分之一，也就是1/100米。

师：如果用小数表示，怎么表示？

生4：0.01米。

师：现在你知道0.01米表示的含义了吗？

生4：把1米平均分成100份，其中的l份，就是0.01米。

师：你为什么想到把1写在这个位置？

生5：现在平均分成100份，说明比分成10份要更小。

师：0.04米、0.12米表示什么意思？观察这些分数和小数，你有什么发现？

生6：读的方法都一样，小数部分都是一个一个读出来的。

生7：都表示了百分之幾。

师：一位小数不够用了，我们继续平均分，用两位小数精确地表示了蚂蚁走的米数。分母是100的分数可以写成两位小数，两位小数表示分母是100的分数。

在蚂蚁竞走的情境下，研究两位小数的意义，在学生根据分数的意义发现0.01表示的意义后，设计探究活动，让学生通过个体探究、小组交流等形式，明确两位小数的意义。

三、经历抽象，探究概念本质

在本节课的教学中，从一位小数和分数的理解引入小数意义的概念，探寻小数是十进分数的本源，抓住了测量的需要与小数产生之间的融合点，从将1米平均分成10份、100份、1000份……中感受小数产生的过程，并结合计量单位之间的进率联想出1千克、1升，从而抽象出只要把整数“1”平均分成10份、100份、1000份……都可以产生小数，帮助学生建立小数概念。

【教学片段3】借助经验迁移，探究概念。

师：我们在认识一位小数的基础上认识了两位小数，并知道了一位小数表示十分之几，两位小数表示百分之几，根据这两个结论，你还能想到什么？

生1：三位小数表示千分之几，四位小数表示万分之几。

师：能在米尺上找到三位小数吗？

生2：把1厘米平均分成10份。

师：把1厘米再精细地平均分，得到毫米，那么1米就被平均分成了多少份？

生3：1000份，1毫米就是1米的1/1000，也就是0.001米。

师：还能在米尺上找出另外一个三位小数，并说说它表示的含义吗？

师：除了米尺上有0.001米以外，还有哪些学过的计量单位之间也类似的关系？

生4：质量单位中的千克和克、容量单位中的升和毫升、长度单位里的千米和米等都有这样的关系。

师：只要把它们都看成整数“1”，平均分成1000份，就可以得到0.001。

生5：分母是10、100、1000……的分数都可以用小数表示。

三位小数的教学是完全建立在学生学习一位小数、两位小数的经验之上的，是将新旧知识进行同化的过程。学生感悟了小数和分数之间存在的本质联系，又勾连了整数和小数之间的十进制关系，开放的课堂更加调动了学生学习的主动性和能动性。教学中，学生通过猜想、验证，明确了三位小数和千分之几之间的内在联系。

四、知识融通，整合数的概念

小数的学习必须在数的体系中去理解，将整数“1”凸显出来，它可以是一个计量单位，也可以是一个图形……借助数形结合进行抽象，启发学生对小数、整数与分数之间的关系进行融合，从而加深学生对小数的理解。

在学生总结出小数意义的基础上，引导学生发现1/10、1/100、 1/1000……乙间存在的规律，引导学生思考整数学习过程中是否也存在这样的关系，促进学生通过观察、比较、发现，将整数、分数与小数进行自然融通，勾连数与数之间的关系，形成对数的组成的初步感知。

【教学片段4】把握知识融通，整合概念。

师：观察0.1、0.01、0.001这些小数，它们有什么规律吗？

生1：0.1、0.01、0.001之间依次是10倍的关系。

师：我们熟悉的整数里是否存在这样的关系呢？（课件依次出现10、100、1000……）看来小数和整数的关系同样密不可分。

师：如果把正方形看作整数“1”，你能涂色表示出这些小数吗？

师：涂完后，你有什么发现？

生2：0.5和0.05表示的意义不同。0.5和0.50大小相等，意义不同。

师：不但正方形里有小数，正方體里也有我们今天学习的小数。你能把涂色部分用小数表示出来吗？

生3：0.9表示把正方体平均分成10分，表示这样的9份。0.09表示…-.

师：如果合并三个小数，会是什么样子？知道现在表示多少吗？没涂色的部分是多少？

生4：合起来刚好就是整数“l”……

将小数与整数进行沟通，丰富了学生对小数意义的理解。通过数形结合，从正方形到正方体，学生逐步抽象，把握本质，感悟到整数“1”的表现形式不同，小数的表现形式也有所不同。

综上所述，在小学高年级数学概念教学中，应当基于学生的年龄和认知特点，使用同化的方式帮助学生获取数学思维方式，通过对概念教学内容的整体性、系统化设计，让学生在生动、实际、探索的数学活动中理解数学概念本质，发展数学关键能力。

（责编黄春香）