基于窗口傅里叶变换的线性相位误差抑制

陈 瑜，潘永强*，刘丙才，田爱玲，李 靓

(1.西安工业大学 光电工程学院，西安 710021； 2.教育部薄膜与光学制造技术重点实验室, 西安 710021)

1 引 言

光学干涉测量作为一种非接触测量方法被定义为新世纪精密测量技术的重要发展方向。相位提取是光干涉测量过程中的关键技术，干涉图的相位测量精度直接影响后续面形精度[1]；传统相位提取技术主要有相移法(Phase-shifting Technique,PST)和傅里叶变换算法(Fourier Transform,FT)[2]，但其在实际应用中各有局限性[3-5]。为克服这一缺点，研究人员提出将窗口傅里叶变换(Windowed Fourier Transform,WFT)应用于相位提取技术中，在一定程度上解决了传统算法的不足，实现了信号局部分析[6]。

窗口傅里叶变换相位提取法是一种空频分析法，其不但可以考虑到局部细节，还可以降低噪声对图像信号的影响，获得较高的提取精度[7]。需要说明的是，在窗口覆盖区域内，条纹幅度被假定为恒定，同时假设相位亦是恒定的，因此，局部频率也应为恒定[8]。而在实际条纹图中，条纹图案的相位一般为非线性分布，这就导致在相位提取中存在了线性相位误差，影响后续相位提取精度。研究者对此情况下的线性相位误差进行了抑制尝试：Chong Yang[9]等人对WFT算法的窗口尺寸选取进行了研究，推导窗口尺寸与二阶相位导数的关系，通过对理论推导的窗口尺寸进行仿真分析验证了其选取依据较传统算法对线性相位误差有抑制效果；钱克矛[10]结合对窗口尺寸的理论推导，根据不同类型条纹的特点及其噪声因素的影响，研究在不同窗口尺寸变换下条纹图案的去噪问题，认为针对非线性度较大的干涉图案，选取小尺寸窗口(σ≤10 pixel)可抑制条纹线性相位误差。以上研究均通过对窗口尺寸进行了调整从而达到抑制线性相位误差的作用，发现在空域内选取小尺寸窗口可使范围内条纹信息成分近似线性，从而抑制线性相位误差。但由于窗口傅里叶变换是一个空频联合域处理技术，其在空域内的小尺寸窗口转换到频域内范围激增，导致该窗口区域内频率分辨率下降，且在窗口范围内的频谱成分中，低频成分易受背景光强干扰导致相位连续性降低，使线性相位误差在抑制的同时受到新的因素干扰，故在WFT技术处理之前对输入条纹的背景光强进行滤除显得尤为重要。

本文基于WFT相位提取算法在实际操作过程中存在的线性相位误差问题进行研究，具体研究过程为：(1)在传统WFT相位提取算法原理基础上，推导利用空频联合分析法滤除背景光强的数学理论。(2)开展仿真实验，首先确定可使WFT技术中线性相位误差抑制度达最大时的窗口尺寸选取依据，其次基于理论推导及仿真得出的最优窗口尺寸对线性相位误差做综合抑制，通过与传统线性相位误差抑制作用下的WFT算法精度进行对比，评价其线性相位误差的抑制程度。(3)对大口径抛物面进行面形重构，通过实验验证本文线性相位误差抑制技术可解决传统WFT技术在抑制线性相位误差时存在的问题并将该技术运用在相位提取算法中，实现算法精度的提高。

2 基本理论

2.1 窗口傅里叶变换理论

对于二维信号f(x,y)，其光强分布表达式:

f(x,y)=a(x,y)+

b(x,y)cos(φ0(x,y)+f1x+f2y),

(1)

其中：a(x,y)为干涉条纹的背景光强分布，b(x,y)为其对应调制度分布，φ0(x,y)为含有待测波面相位信息的初始相位分布函数，f1,f2分别为沿x,y方向的载频成分[11]。

其对应窗口傅里叶谱分布表达式可表示为

(2)

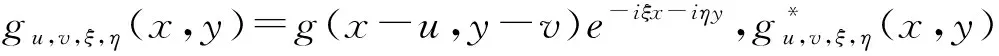
(3)

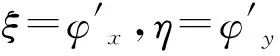
(4)

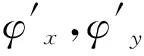
(5)

如式(4),在窗口覆盖范围内定位可使频谱分布值达最大时的自变量值ξ,η，将该值赋给该区域相位的局部频率(相位导数)，通过移动窗口表征整幅干涉图案从而获取相位[14]，这就使频谱成分中谱值能量相对较低的噪声成分被抑制，相较于传统傅里叶变换相位提取算法，WFT算法有良好的去噪能力。

2.2 背景光强的傅里叶空频分析法

根据傅里叶变换空频分析法，对空域内的二维信号f(x,y)做傅里叶变换，得到其频谱分析:

F(f1,f2)=A(f1,f2)+C+(f1,f2)+C-(f1,f2).

(6)

一般地，对于载频条纹(1)，其频谱分布主要包含等式(6)右侧三项，从左至右依次是干涉图案背景光强的频谱分布(或称为零级谱函数A(f1,f2))、正一级频谱的分布函数C+(f1,f2)、负一级频谱的分布函数C-(f1,f2)。选取一个中心频率为(f1,f2)的滤波器将正一级频谱提取出来并平移至原点，得到滤除背景光强干扰的正一级频谱分布，并对其进行二维傅里叶逆变换转换到空域内[15]，即:

(7)

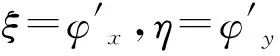
(8)

同理根据式(5)得，后续相位值为:

φ(u,v)=∠max|SF[u,v;ωx,ωy]|.

(9)

对比式(4), 此方法可实现相位提取，得到的频谱谱值仅为传统WFT相位提取中谱值的0.7倍，一般地，干涉条纹的背景光强在整个频域内占据较高的幅值，而通过傅里叶空频分析法将其滤除，降低了高谱值背景光强的影响，提高窗口傅里叶脊值的提取精度，从而恢复真实相位，并保留WFT技术良好的去噪能力。

3 仿真分析

3.1 最优窗口尺寸判定

为确定可使线性相位误差抑制度达到最大时的窗口尺寸选取依据，对WFT技术的窗口尺寸进行仿真判定。定义相位绝对误差如式(10)，通过对相位绝对误差的计算分析线性相位误差对干涉信号的影响程度，其中φ0为初始仿真相位，φ为经相位提取算法提取出的相位N为所处理干涉图的尺寸，本文中所用干涉图案均为300×300 pixel。

Δφ=1/N·sum(φ0-φ).

(10)

仿真干涉条纹图A，对其引入水平方向载频增加条纹非线性度如式(11)。变换窗口尺寸取值区间为[1,30]，计算每一尺寸下的Δφ的值，为避免由于窗口尺寸过大引入的边缘效应问题，仅选取条纹图中心区域(如图1)进行计算，绘制对应σ-Δφ曲线趋势图如图3的Phase error A所示。

fA(x,y)=255+10cos(φ(x,y)+2x).

(11)

图1 仿真干涉图 AFig.1 Simulated interferogram A

在实际干涉图案中，噪声成分渗透干涉图案整个区域，为使研究更具严谨，对条纹图案进行加噪处理，通过仿真分析确定在此情况下的窗口尺寸选取准则。仿真样本选取干涉图案A并引入均值μ=0，σ=1的高斯白噪声如图2所示，计算不同窗口尺寸下的相位绝对误差，并绘制对应σ-Δφ曲线趋势图如图3的Phase error B所示。

图2 仿真干涉图 A(加噪)Fig.2 Simulated interferogram A

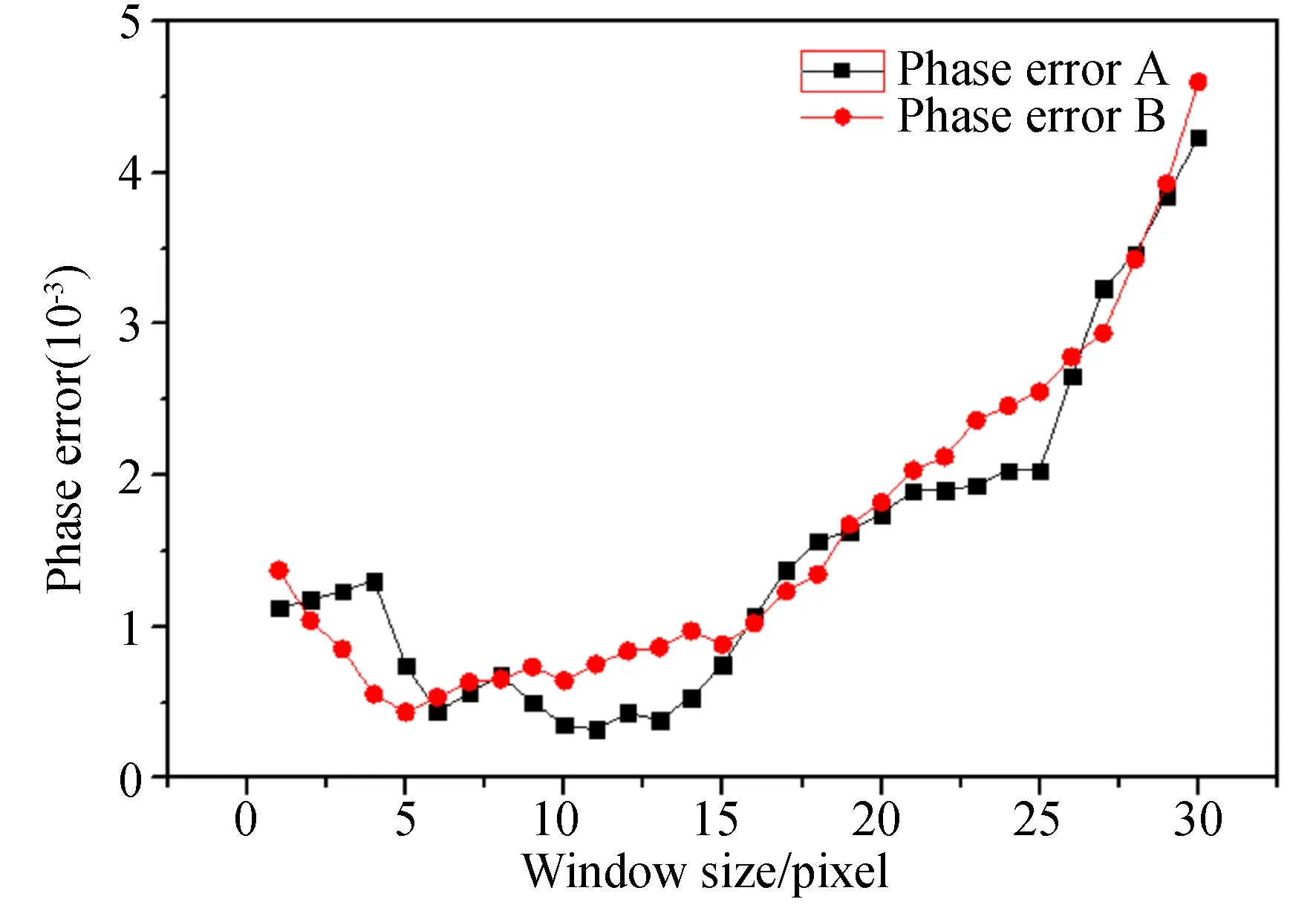
图3 不同窗口尺寸下干涉图相位残差曲线Fig.3 Phase residual curve of interferogram under different window sizes

通过对图3的分析可知，在综合了噪声因素的情况下，两条曲线趋势相似。分析其主要原因为，WFT相位提取技术主要针对某一区域内的条纹图提取局部频率并最后获取所需相位，在操作中可对局域内噪声起到良好的消除作用，因此噪声因素对其相位提取精度影响不大，确定可对线性相位误差抑制程度最大的窗口选取依据为小尺寸窗口(σ=5 pixel)，缩小了传统线性相位误差抑制技术的窗口尺寸判定范围。

3.2 线性相位误差抑制度对比

为验证本文提出的线性相位误差抑制技术的可行性，仿真如图4(a)所示一维信号，长度为1×300 pixel，添加水平方向非线性度及噪声，图4(b)为该信号对应的初始相位导数分布曲线。分别利用传统线性相位误差抑制技术及本文提出技术应用于图4(a)一维信号的WFT相位提取处理中，选取可以反映相位变化率的相位导数(局部频率)为对比参量，通过比较两种技术处理下得到的相位导数分布情况研究不同方法对线性相位误差的抑制程度。两种技术处理过程分别如下[6-7]：传统线性相位误差抑制技术可通过选取小尺寸窗口(σ≤10 pixel)实现抑制条纹中线性相位误差的作用，同时结合本文3.1分析，选定在窗口尺寸σ=5 pixel时为传统线性相位误差抑制技术的窗口尺寸选取，图4(e)为经该方法提取的相位导数。

采取本文提出方法，首先对初始信号进行预处理，即滤除背景光强干扰同时保留包含相位成分的正一级频谱，图4(c)为经FT变换得到的初始信号的频谱分布，其背景光强所在位于(151,0)处，选取中心频率为(74,0)的矩形滤波窗将虚线区域内所示的正一级频谱滤出并移至中心位置如图4(d)，对其做傅里叶逆变换后得到时域内的信号成分并对其做后续WFT相位提取处理，此处窗口尺寸选取抑制线性相位误差程度达最大的σ=5 pixel，提取相位导数结果图4(f)，通过对图5中仿真所获相位导数进行分析。

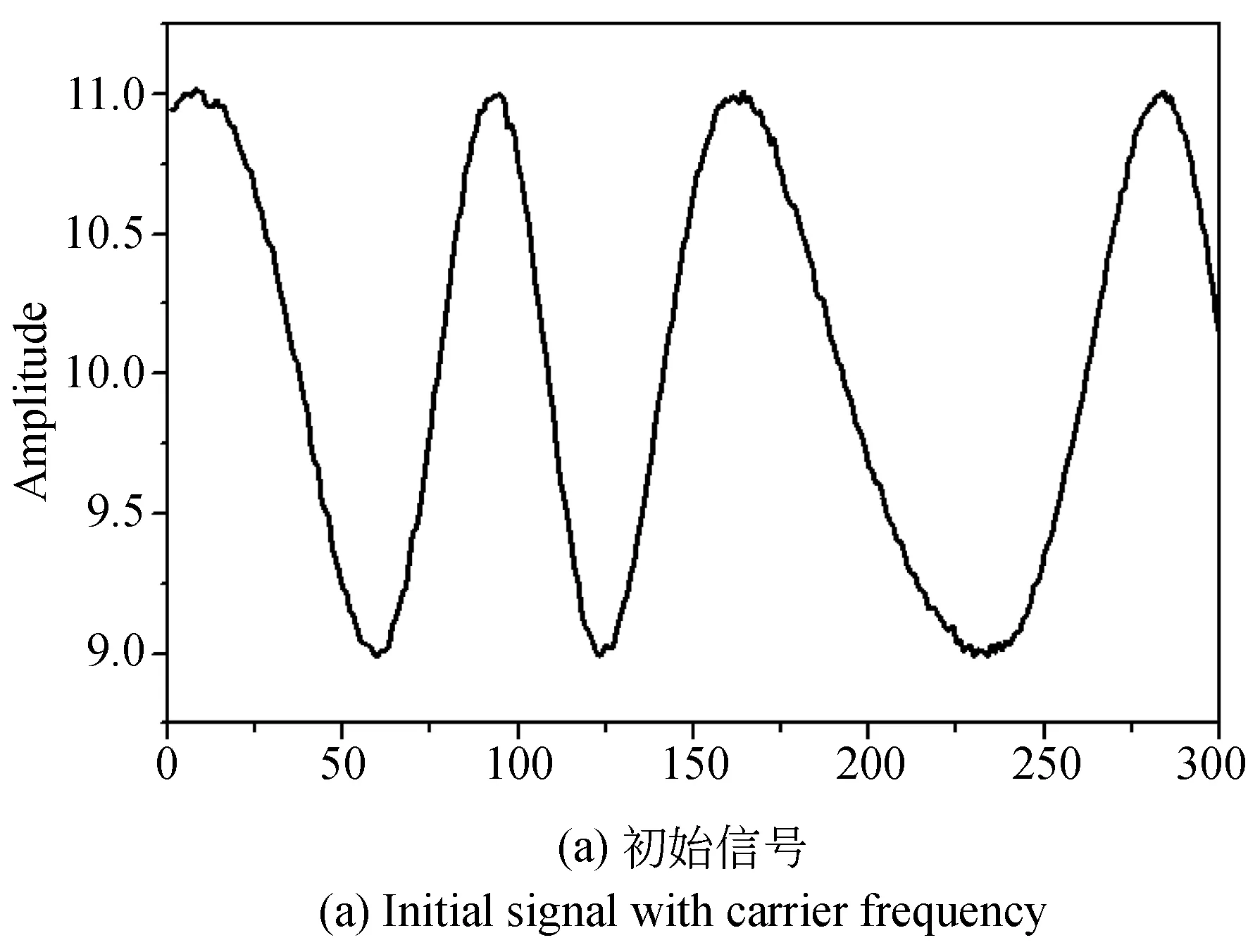
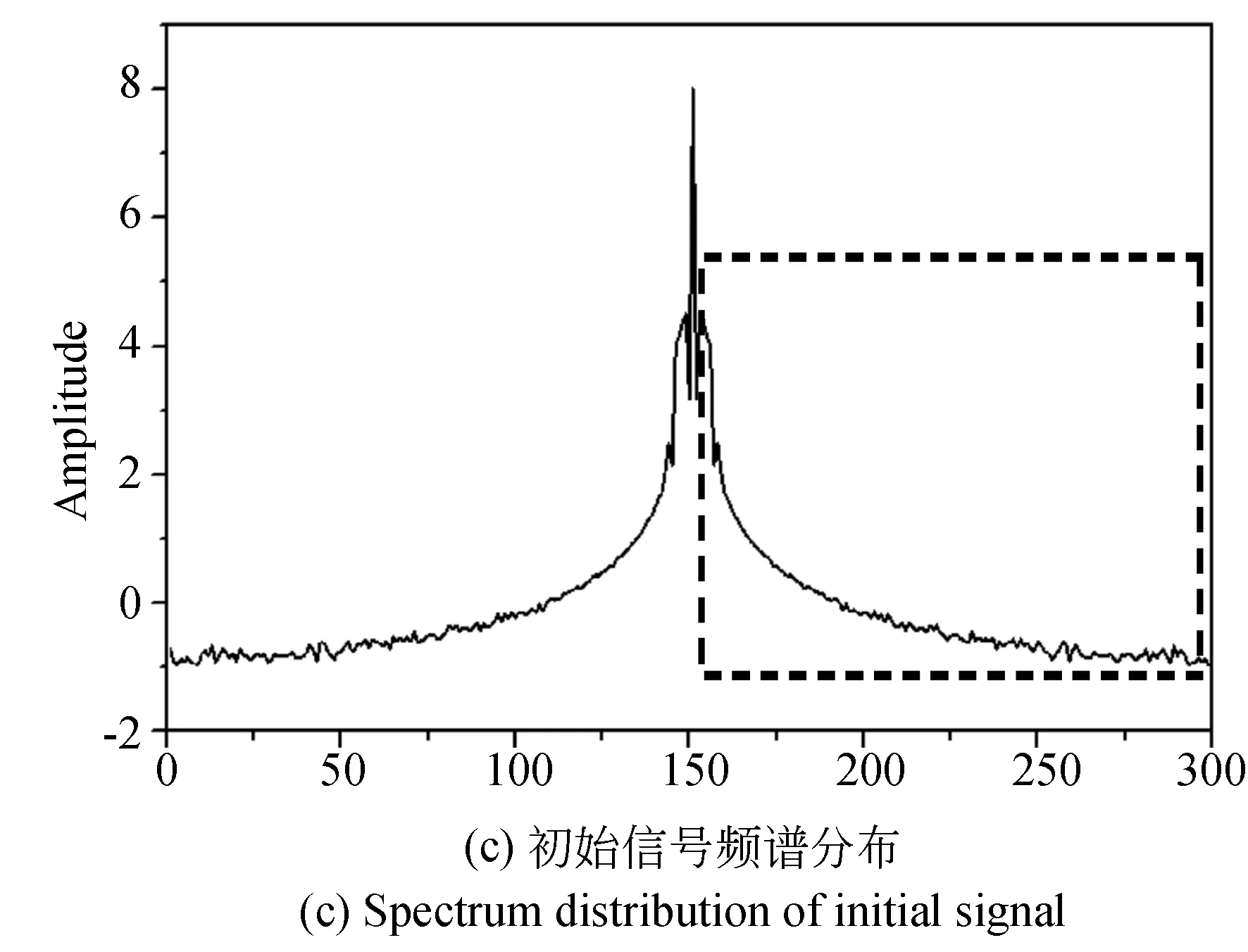
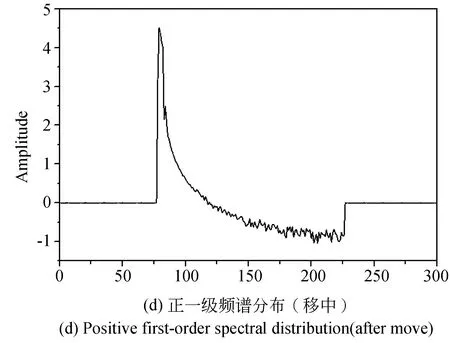
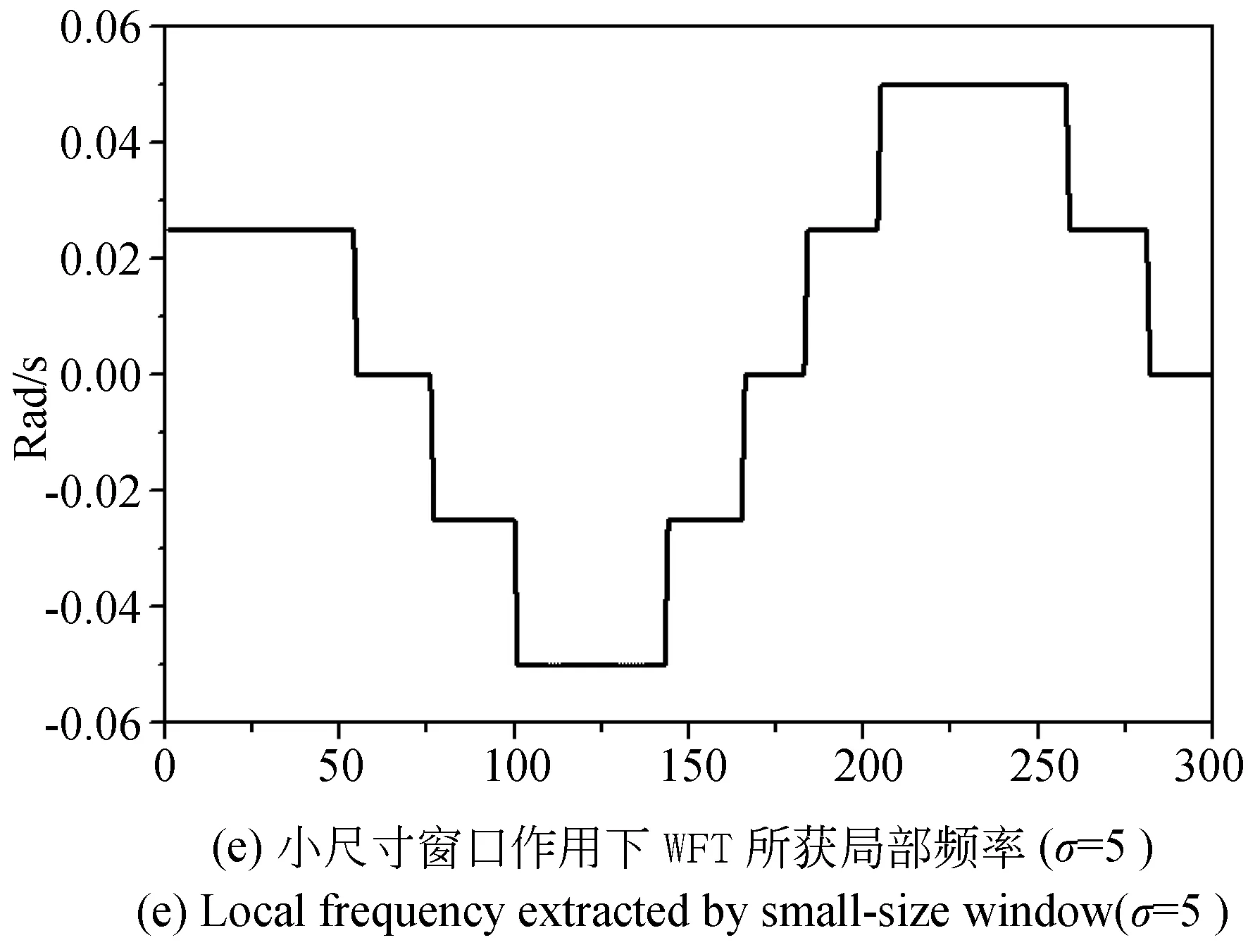
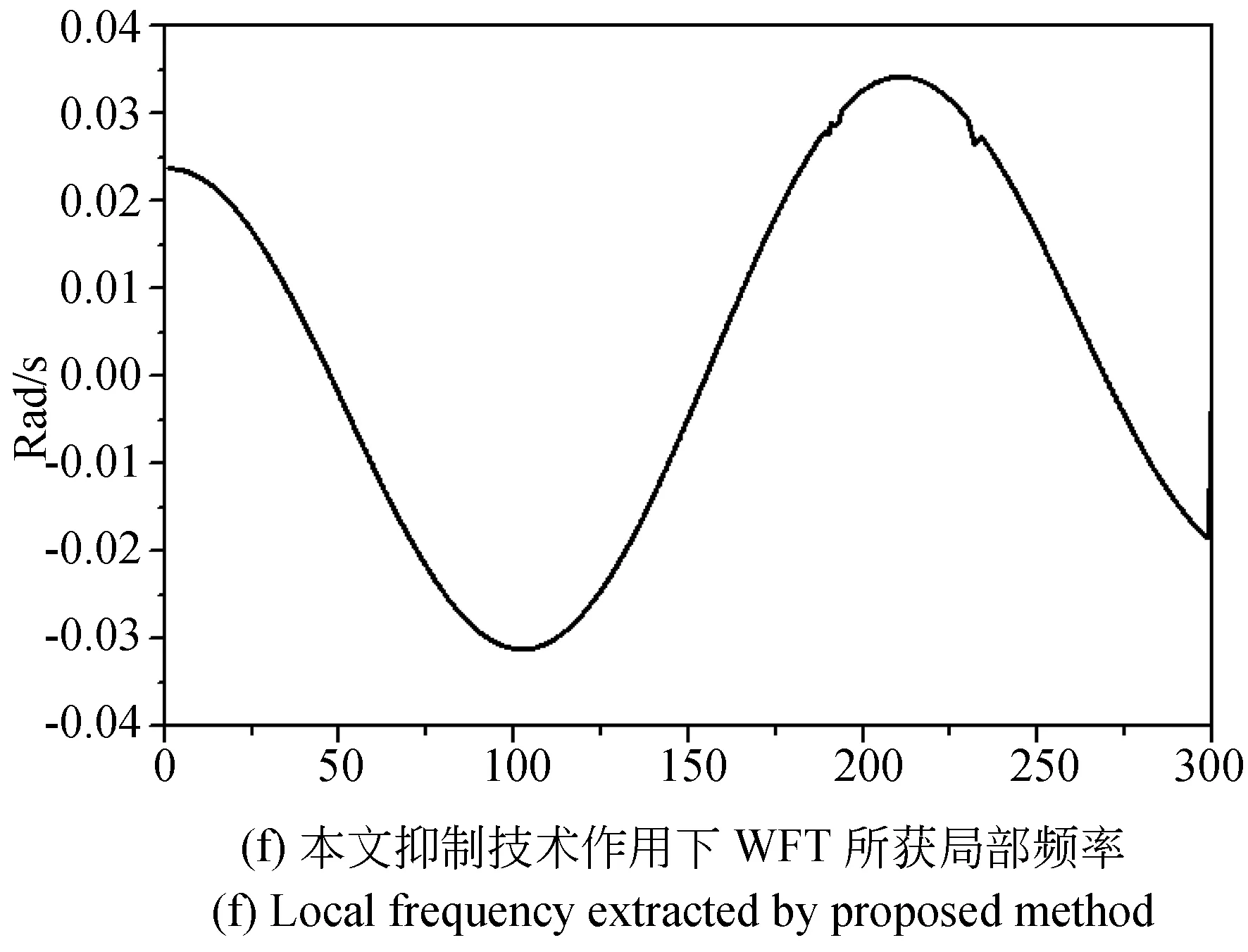
图4 不同线性相位抑制技术作用下相位导数提取结果图

传统WFT法选取小尺寸窗口(σ=5 pixel)以达到抑制线性相位误差的作用，所获相位导数(局部频率)如图4(e)所示，对比初始相位导数如图4(b)有很大偏差，分析其原因可能为选取小尺寸窗口降低了窗口范围内条纹信息的非线性度，从而达到降低线性相位误差的效果，但空域内小尺寸窗口在频域内尺寸变大，某些低频成分受背景光强的干扰，导致相位变化不明显，相位一阶导数(局部频率)在某些区域处于稳定值，此处相位不发生变化。

本文提出的抑制线性相位误差技术，在利用小尺寸窗口(σ=5 pixel)削弱条纹非线性度引入的误差的同时通过空频联合分析法消除了背景光强干扰，提取相位的局部频率如图4(f)所示，相较于传统线性相位误差抑制技术，其处理所得相位一阶导数更接近初始相位一阶导数(局部频率)。

4 实验验证

为验证仿真结果的可行性及精度，对大口径抛物面型进行面形重构实验，实验阶段所用菲索干涉仪为美国Zygo公司生产的Verifire PE激光干涉仪，该干涉仪是共光路面形计量干涉仪，光源为低功率的632.8 nm的氦氖激光，其干涉仪装置如图5，采用PZT移相干涉装置可对光学元件面形进行检测。

图5 Zygo激光干涉仪实验装置图Fig.5 Zygo laser interferometerdevice diagram

图6 实验采集干涉图(截取图)Fig.6 Experimental interferogram(intercept diagram)

图6为Zygo干涉仪采集实验干涉图，为便于计算机离散化处理，将圆域干涉图截取为300×300尺寸矩形干涉图，通过对比重构面形中波面评价参数，验证传统线性相位误差抑制技术及本文所提方法对WFT相位提取精度的影响。为直观线性相位误差影响效果，图7(a)～图7(c)分别为WFT算法在σ=3 ,5,10 pixel作用下生成的包裹相位图，图7(d)为本文提出的线性相位误差抑制技术作用下WFT算法所获包裹相位图。

图7 不同线性相位误差抑制技术下WFT算法处理所获包裹相位图Fig.7 Wrapped phase obtained by WFT algorithm under different linear phase error suppression techniques

对图7(a)～图7(c)中包裹相位图进行分析可知，选取不同窗口尺寸作用得到的包裹相位均存在线性相位误差影响，其中图(a)为选取小尺寸窗口作用下，频谱中低频成分受到背景光强影响致使相位在某些区域出现相位模糊的现象。图(b)在选取较大的窗口尺寸时，窗口区域内非线性度增加，导致图中所示相位缺失现象；选取窗口尺寸σ=5 pixel时的作用效果最佳如图(c)所示，但中心区域及边缘仍有模糊现象，即少部分频谱成分受到背景光强干扰；采取本文提出的线性相位误差抑制技术处理所获包裹相位如图(d)，较传统小尺寸窗口抑制作用下的WFT算法所获相位结果更清晰。为增加实验结果的可信度，对上述4种包裹相位进行最小二乘法解包裹处理获得连续相位，并通过Zernike拟合生成如图8(a)～图8(d)所示的面形分布。

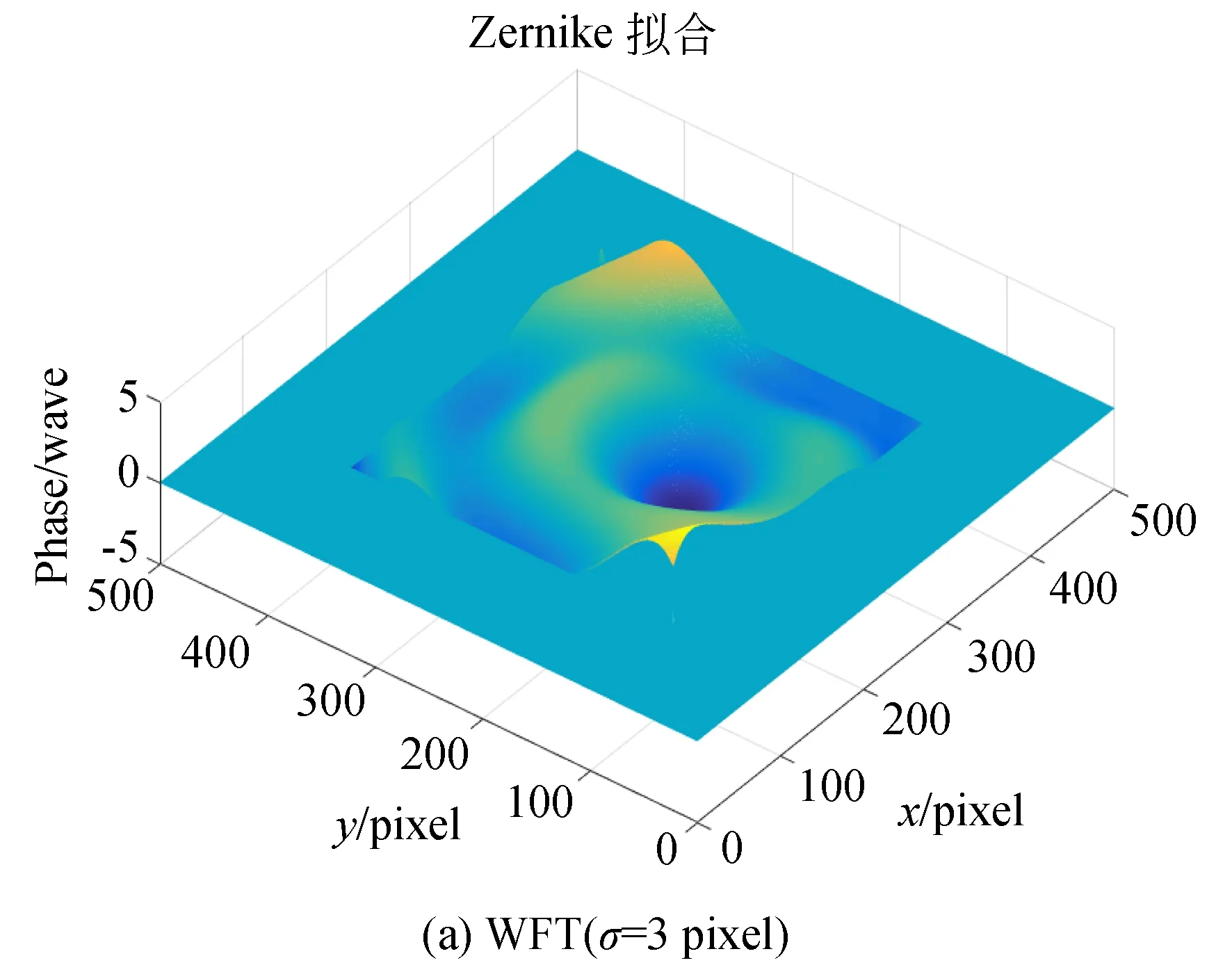
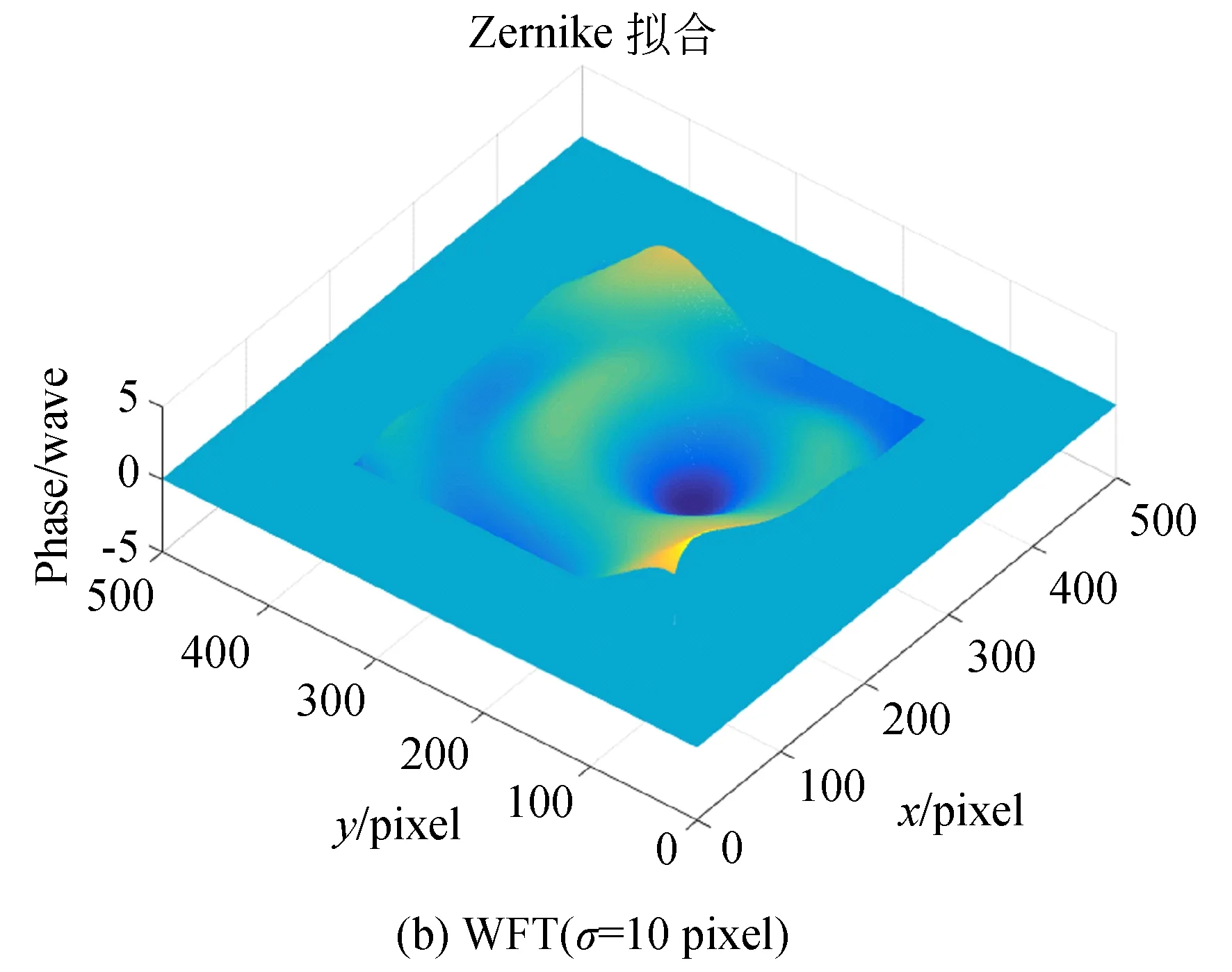
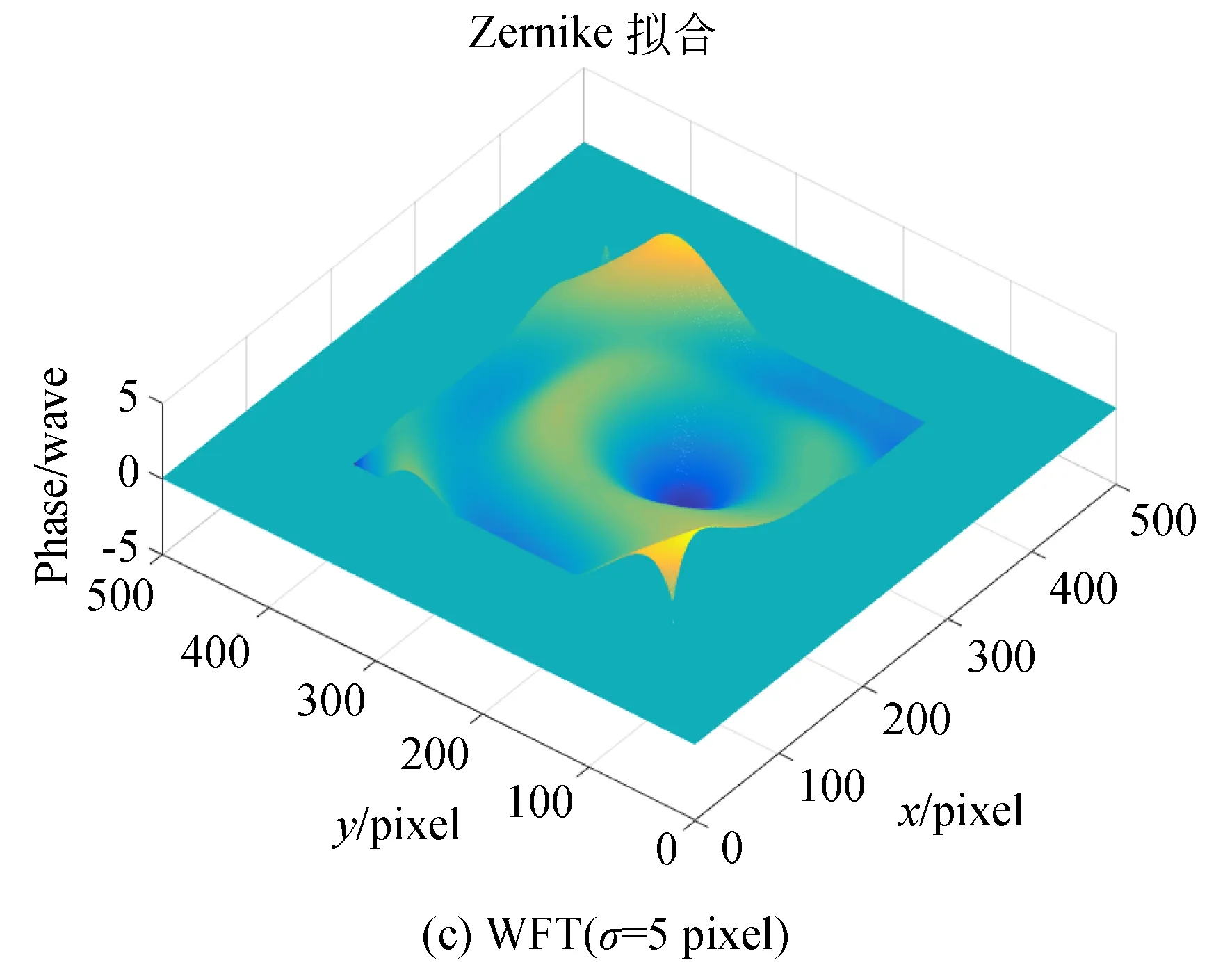
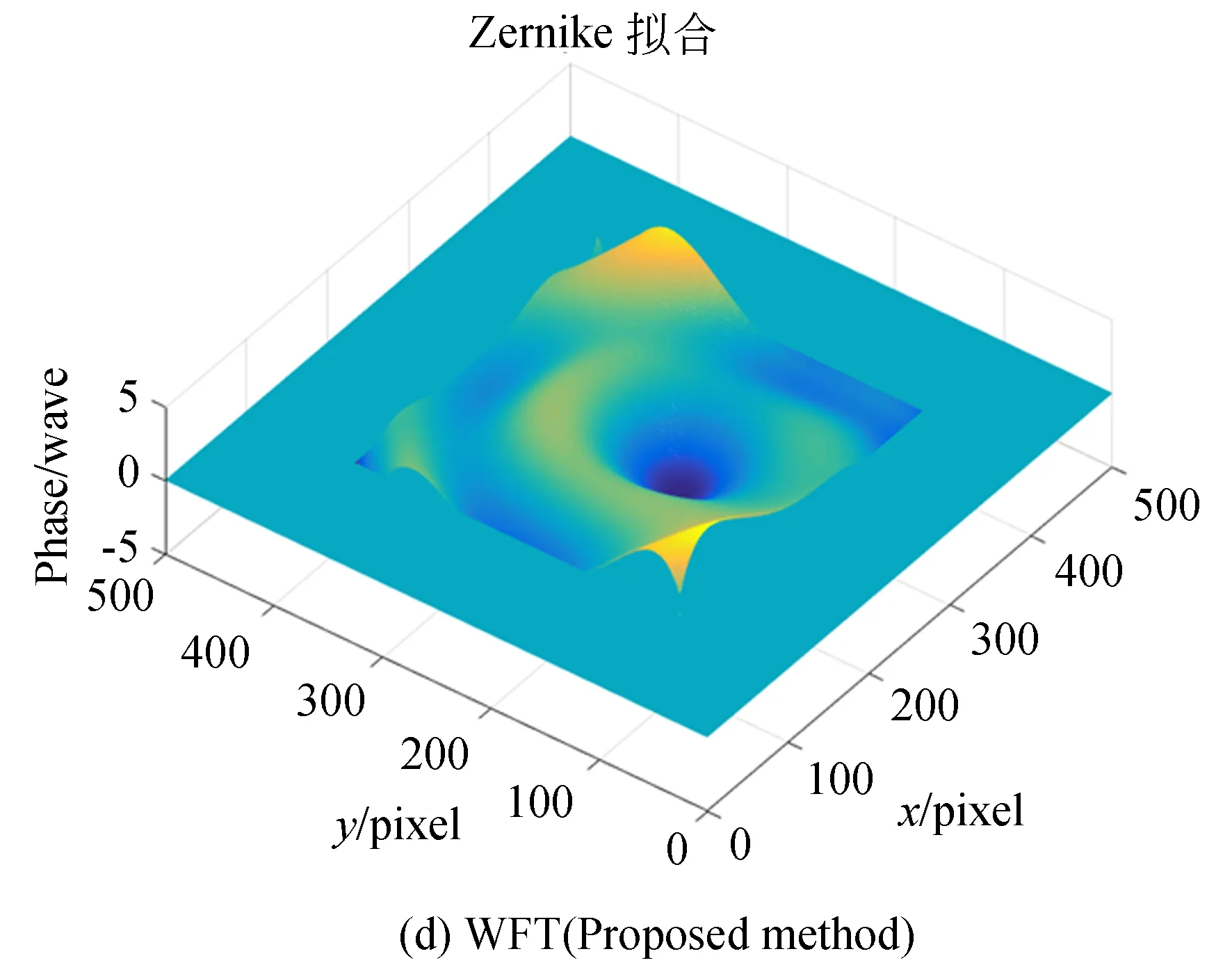
图8 不同线性相位误差抑制技术下WFT算法所获波面分布

分析图8可知，受线性相位误差影响较大程度的包裹相位经拟合生成的波面(如图8(a)～图8(b)较图8(c)～图8(d)在边缘处有偏差。为量化数据处理过程，对以上4种面形的波面评价参数PV，RMS进行计算，并与Zygo干涉仪所测数据进行残差计算，分别记为ΔPV及ΔRMS，并记录如表1。

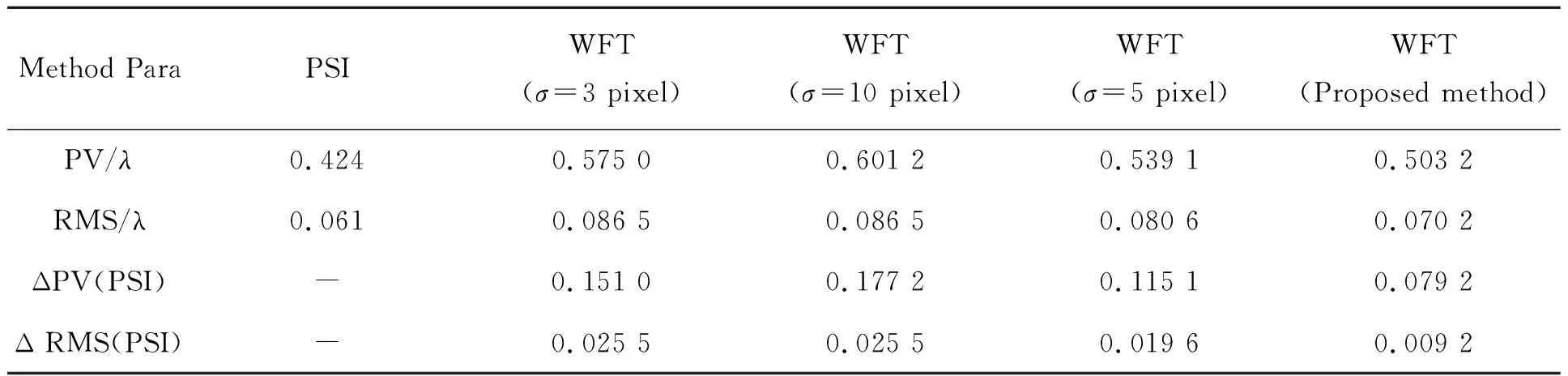
表1 Zernike拟合生成波面评价参数汇总(λ=632.8 nm)

对表中数据进行分析，在选取窗口尺寸为σ=3,10 pixel时，线性相位误差影响较大，致使后续相位提取精度在面形参数上较相移干涉技术偏差较大。在σ=5 pixel时线性相位误差影响最小，其在面形拟合上评价参数的残差值较σ=3,10 pixel时降低，即在传统线性相位误差抑制技术时，σ=5 pixel可达到最优线性相位误差抑制效果；采用本文提出的线性相位误差抑制技术作用生成的面形与相移干涉技术残差达到最小，较传统线性相位误差抑制技术得到了提升。

5 结 论

本文针对传统WFT相位提取算法中选取小尺寸窗口抑制线性相位误差的传统技术进行改进，提出了一种利用空频联合分析法对干涉图案频谱成分进行预处理，使低频成分不受背景光强干扰的线性相位误差抑制技术，并利用仿真分析确定了可使线性相位误差抑制度达最大时的最优窗口尺寸选取准则，结合以上两种作用效果对WFT相位提取技术中线性相位误差做综合抑制，仿真及实验的对比分析均表明，本文提出方法较传统线性相位误差抑制技术的抑制程度得到了提高，抑制效果体现为算法重构面形精度与相移干涉技术的PV残差值由0.115 1λ降低到0.079 2λ，波面均方根残差值由0.019 6λ降低到0.009 2λ。