二阶区间值积分微分方程初值问题解的存在唯一性
郭雅婷,叶国菊,刘 尉,赵大方
(河海大学理学院, 中国 南京 210098)
区间分析是一门用区间变量代替点变量进行运算的数学分支, 是一种解决不确定性问题的有效方法。起源于计算数学的误差理论。自Moore 系统地提出区间分析理论以来, 该理论被广泛应用于数学[1]、计算机[2]、控制理论[3, 4]等领域。近年来,Viegas[5],Chen[6]和Li[7]等学者又在航空、机械工程领域获得了新的研究成果。
在经典的实分析中, 最重要的概念之一是实值函数的导数。相应地, 在区间分析中, 为进一步建立区间值函数微分理论, 各种导数概念相继出现。其中,文献[8]提出的Hukuhara 导数引起广泛关注。然而,运用Hukuhara 导数会导致解的区间宽度随时间的增加而增加,因此,区间值微分方程也尚未被很好地理解和应用。直到2009年, Stefanini和Bede提出的广义Hukuhara 导数有力地解决了这个问题[9], 对研究区间值微分方程提供了很大帮助。
区间值微分方程作为描述不确定性系统的一种重要方式, 在区间分析理论中的重要性日益凸显。随着广义Hukuhara 导数的建立, 区间值微分方程理论得到进一步发展。为探讨区间值微分方程解的存在性及唯一性, Villamizar, Long和An 等学者利用经典Banach 不动点定理和弱压缩映射原理研究偏序空间的方程[10-16]。但弱压缩映射原理尚未应用于二阶区间值积分微分方程。受文献[10-16]启发, 本文利用广义Hukuhara 导数以及弱压缩映射原理研究二阶区间值函数积分微分方程初值问题, 并给出例子验证结果的正确性。方程形式如下:
(1)
式中X(t),K(t):J→Kc()是区间值函数,G(s,X(s)):J×Kc()→Kc()也是区间值函数,Kc()是由上的闭区间构成的空间, 即Kc() = {[a,b] |a,b∈且是X的二阶广义Hukuhara导数,I1,I2∈Kc()。
1 预备知识
任取Kc()中的元素A,B, 其中对任意λ∈,Kc()空间中的区间运算规定如下:
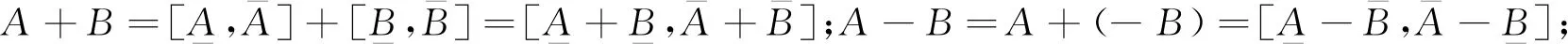
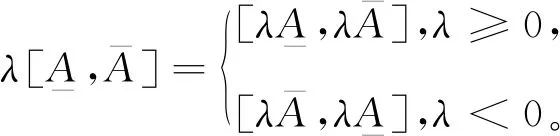
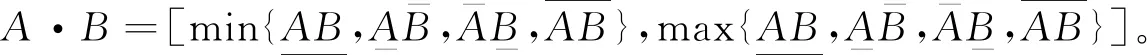
(2)
同时,Kc()中的Kulisch-Miranker 偏序关系”⪯ ” 定义为: 对任意的(),

(3)
实数是区间的特殊形式, 称为退化区间。例:2=[2,2]。设A,B∈Kc(),它们之间的Hausdorff 距离定义为空间(Kc(),H)是一个完备的, 局部紧的, 可分的度量空间。
设A,B∈Kc(),如果存在C∈Kc(),使得A=B+C, 则称C为A和B的差, 记为C=A⊖B,注意A⊖B≠A+(-B)。只有当w(A)≥w(B)时,A⊖B有意义。因为⊖有很大局限性, 文献[12]中提出了⊖g使得:
定义1[17]设X:[a,b] →Kc()是区间值函数, 若对任给的ε> 0,总存在某一个δ=δ(t,ε)>0,使得对所有的s∈[a,b], 当|t-s| <δ时, 都有
H(X(t),X(s))<ε
成立, 则称X在t∈[a,b]上连续。
定义2[10]若对区间值函数F(t):[a,b] →Kc(),对任意t∈[a,b], 存在实数M,有H(F(t),{0})≤M,则称区间值函数F(t) 在[a,b]上有界。
引理1.[18]设F,G∈C([a,b],Kc())是两个区间值函数, 若F,G满足偏序关系F≤G,则对任意的A∈Kc()有
根据以上引理可以得到
定义3[10]设X:[a,b]→Kc()是区间值函数, 如果存在一个(),使得下列任一条件成立, 则称X在t0∈[a,b] 处是一阶强广义可微的。
a.设h> 0足够小,X(t0+h)⊖X(t0),X(t0)⊖(t0-h) 存在且有
b. 设h> 0足够小,X(t0)⊖X(t0+h),X(t0-h)⊖X(t0) 存在且有
c. 设h> 0足够小,X(t0+h)⊖X(t0),X(t0-h)⊖(t0) 存在且有
d. 设h> 0足够小,X(t0)⊖X(t0+h),X(t0)⊖(t0-h) 存在且有
注1.在文献[10]定义3 中, 当X(t) 满足条件a时,X(t) 称为(i)型可微; 当X(t) 满足条件b时,X(t) 称为(ii)型可微。
定义4[15]设(X,d)是一偏序空间,F:X→X,对任意的x,y∈X, 若x⪯y时有F(x)⪯F(y), 则称函数F为非减函数。
定义5[19]设函数Ψ:[0,∞) → [0,∞) 满足(a)Ψ连续且非减;(b)Ψ(t)=0当且仅当t=0,则称Ψ为变更距离函数。
定义6[19]设(X,d)是一度量空间, 若存在变更距离函数Ψ和Φ, 使得函数F:X→X满足
Ψ(d(F(X),F(Y))≤Ψ(d(X,Y))-Φ(d(X,Y)),
则称函数F是弱压缩的。
定理1[19]设(X,⪯) 是一偏序空间且存在度量d, 使得(X,d) 是一完备度量空间。若非减函数F:X→X满足:(1)存在变更距离函数Ψ,Φ,对任意XY有Ψ(d(F(X),F(Y))≤Ψ(d(X,Y))-Φ(d(X,Y));(2)X中存在非减序列(Xk)k∈N→X或F连续;(3)存在X0∈X, 有X0⪯F(X0) 或X0F(X0)。则F有唯一的不动点。
2 主要结果
定理2a.当X(t):J→Kc()连续且X和是(i)型可微时, 方程(1) 等价于
(4)
b.当X(t):J→Kc()连续且X是(ii)型可微,是(i)型可微时,方程(1)等价于
(5)
c.当X(t):J→Kc()连续且X是(i)型可微,是(ii)型可微时,方程(1)等价于
(6)
d.当X(t):J→Kc()连续且X和是(ii)型可微时,方程(1)等价于
(7)

进而有
以上仅给出了式(7) 的证明, 剩余3种情况类似可得。
定义7若区间值函数X(t):J→Kc()满足方程
则称X(t)是方程(1)的(i)-(i)型解;

注2.由定理6 中方程的4种形式及定义7 和定义8 得方程(1) 的解和下解均有4种形式, 分别为(i)-(i),(i)-(ii),(ii)-(i)和(ii)-(ii) 型, 本文将其简记为(a)-(b)型解。
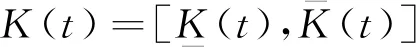
K(t)G(t,X(t))⪯K(t)G(t,Y(t)),
(8)
H(K(t)G(t,X(t)),K(t)G(t,Y(t)))≤MH(G(t,X(t)),G(t,Y(t)))。
(9)
证明:由式(2)和(3)得


成立, 故式(8)成立。由K(t)有界, 存在M使得
H(K(t)G(t,X(t))),K(t)G(t,Y(t)))≤H(MG(t,X(t)),MG(t,Y(t)))≤MH(G(t,X(t)),G(t,Y(t)))。所以式(9)成立。
定理3若方程(1) 存在(a)-(b) 型下解μ∈C1(J,Kc()),区间值函数F(t),K(t),G(t,X(t))连续且满足:
a.G(t,X(t))关于X(t)为非减函数, 即,若XY,则G(t,X(t))G(t,Y(t));
b.K(t)为界区间值函数,且K(t)0;
c.G(t,X(t))是弱压缩的,即,存在变更距离函数Ψ,Φ,使得对任意XY,有
Ψ(H(G(t,X(t)),G(t,Y(t)))) ≤Ψ(H(X(t),Y(t))) -Φ(H(X(t),Y(t))),
则方程(1)存在唯一的(a)-(b) 型解。
证明:由定理2 知解有4种类型:(i)-(i) 型解, (i)-(ii) 型解, (ii)-(i) 型解, (ii)-(ii) 型解。不失一般性, 以下讨论(ii)-(ii) 型解的存在性, 其他3种解的存在类似可证。定义算子A:C(J,Kc()) →C(J×Kc(),Kc()) 如下:
若X∈C(J,Kc()) 是A的不动点, 则X是方程的(ii)-(ii)型解。下证算子A有唯一不动点。
根据条件a及引理1, 对任意XY,
所以A非减。
在C(J,Kc())中考虑k足够大使得以及度量定理中条件c成立, 则对所有XY有Ψ(H(G(t,X(t)),G(t,Y(t)))) ≤Ψ(H(X(t),Y(t))), 由变更距离函数的非减性得H(G(t,X(t)),G(t,Y(t))) ≤H(X(t),Y(t))。(C(J,Kc()),Hk)是一完备度量空间[10]。
根据定理中条件b 及引理2中式(8)和(9)可得

所以有
则存在变更距离函数γ,使得
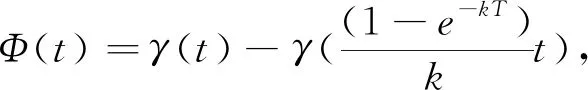
γ(Hk(AX,AY))≤γ(Hk(X,Y))-Φ(Hk(X,Y))。
因为μ是方程(1) 的(ii)-(ii)型下解, 所以有
由定理1得A有唯一的(ii)-(ii) 型不动点, 即方程有唯一的(ii)-(ii) 型解。
注3.若将定理3 条件中的下解存在改为上解存在, 由定理1 得结论仍成立。
3 例子
例1.考虑区间值积分微分方程:
(10)
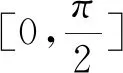
证明:令X(t) =[t,et], 则有
所以X(t)是方程(10) 的一个(i)-(i)型上解。下面验证方程(10) 满足定理3 的条件。
a. 当X(t)⪯Y(t)时,
b. 0⪯K(t)=[t,t+1]⪯3;
则
根据定义5可知存在变更距离函数Ψ,Φ,使得,
经验证方程(10)满足定理3 及注3 中条件, 方程(10)存在唯一的(i)-(i) 型解。

