让学生享受数学的美和挑战

张安军

摘要：数学教师应该利用数学自身的魅力，激发学生学习的兴趣和热情，提高学生学习的动力。《三角形的高、中线与角平分线》一课教学，可以从数学史中挖掘三角形“三线”的相关问题，供学生探索，让学生感受数学的美、接受数学的挑战。相应的教学立意是：挖掘内容元素，让学生体验数学美;创设活动情境，让学生发现、创造数学美;在数学美中孕伏适度的挑战，让学生感到数学好玩。

关键词：数学美数学挑战学习动力《三角形的高、中线与角平分线》

利用数学自身的魅力而不是数学以外的东西，激发学生学习的兴趣和热情，提高学生学习的动力，是反对数学教育“去数学化”的大背景下，数学教师尤其应该努力的一个方向。那么，数学自身的魅力包括什么呢？笔者认为，至少应该包括数学的美和适度的挑战——能带来愉悦感和成就感。

人教版初中数学八年级上册第十一章《三角形》第一节《与三角形有关的线段》第2课时的内容是“三角形的高、中线与角平分线”。由于内容简单而单薄，很多教师在课堂上增加了相应的练习。这虽然填充了课堂的内容，但使得学生学习的兴趣和热情在做题中慢慢减弱。这促使笔者思考：能否从数学史中挖掘三角形“三线”（高、中线与角平分线简称“三线”）的相关问题，供學生探索，让学生感受数学的美、接受数学的挑战？下面，首先呈现基于这一想法的教学设计，然后进一步阐述相应的教学立意，与各位同仁交流。

一、教学设计

（一）化静为动，感受“三线”的对称美

问题1如下页图1，在△ABC中，动点P在边BC上移动。在移动的过程中，有没有你熟悉的线段AP？

追问1你熟悉的线段AP有什么特点？你能用数学符号表示这些特点吗？

追问2你能给出你熟悉的线段AP的定义吗？

追问3三角形的高与垂线、三角形的角平分线与角平分线有何区别？

对于问题1，教师可以利用几何画板动态演示，让学生观察线段AP的变化。学生最容易想到的线段AP是△ABC的边BC上的高，一方面是因为熟悉求三角形面积时需要高，另一方面则是因为审美：两条直线互相垂直是大自然中对称美的体现，也是简洁美（极值）的体现。同样地，中点是线段的对称中心，角平分线是角的对称轴，它们都体现对称美。在点P移动的过程中，让学生在审美的视角下选择特殊位置的线段AP，然后分别对这样特殊的线段进行符号表示、定义提炼以及概念辨析，从而加深对三角形“三线”概念的理解。

（二）动手操作，感受“三线共心”的和谐美与统一美，接受证明的挑战

问题2三角形的中线有几条？请画出或折出三角形所有的中线，你有什么发现吗？

追问1三角形所有的中线相交于一点，那么，所有的角平分线相交、所有的高相交又有怎样的结果呢？你会提出哪些猜想？如何验证？

学生画出（或折出）三角形的中线后，会发现三角形的三条中线相交于一点，并惊讶于这是概率很小的事件，却神奇地发生了。教师指出这个结论在后续的学习中可以证明，激励（而不强求）学生接受证明的挑战。然后，介绍12岁的爱因斯坦第一次读《几何原本》时的感受：

在12岁时，我经历了另一种性质完全不同的惊奇，就是在一个学年的开始，当我得到一本关于欧几里得平面几何的小书时所经历的：这本书里有许多断言，比如三角形的三条高交于一点，它们本身虽然不是显而易见的，但是可以很可靠地加以证明，以至任何怀疑似乎都不可能，这种明晰性和可靠性给我造成了一种难以想象的印象……

接着，让学生通过类比的方法猜想三角形的三条角平分线相交于一点，三条高相交于一点，然后画图验证，从而感受到数学的和谐美和统一美。

（三）联系实际，感受重心的应用美与方法美

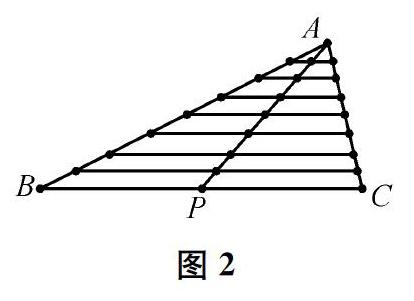
问题3取一根质地均匀的木棒，顶住它的重心，它会保持平衡，那么它的重心分别在哪里？

追问1如图2，把一块质地均匀的三角形木板切成互相平行的一根根木棒，这一组木棒的重心在哪里？

追问2三角形木板的重心在哪里？为什么？请你谈谈你的理解。

当学生惊讶于三角形的三条中线相交于一点时，引导学生发现这个交点非常重要，就是重心，即重力平衡点，并通过微分思想进行理论证明，让学生感悟数学的应用美和方法美。

（四）拓展探索，感受“三心共线”的奇妙美，接受证明的挑战

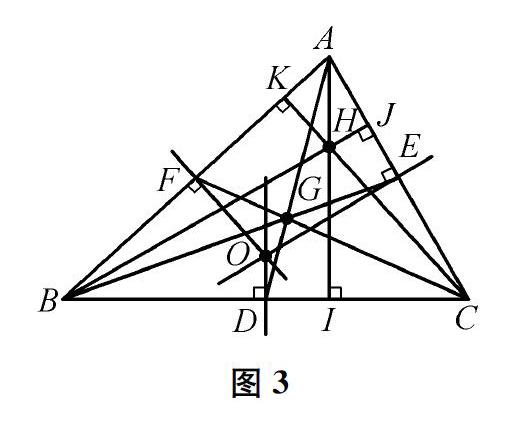
问题4如图3，△ABC的重心为G，垂心（三条高的交点）为H，分别过△ABC各边的中点D、E、F作各边的垂线，交点为O。对于点H、G、O，你有怎样的发现？再任意画一个三角形验证你的想法。

在重心和垂心的基础上，引入外心（不必向学生介绍这一概念，可以为学生后续学习“圆”埋下伏笔）。学生通过操作、观察，能够发现垂心、重心、外心三点共线，从而再次感受数学的奇妙美。教师指出这个结论在后续的学习中可以尝试证明，激励（而不强求）学生接受证明的挑战。然后，介绍这条直线是数学家欧拉发现的，被称作“欧拉线”，鼓励学生勤于思考，善于发现和提出问题、分析和解决问题。

（五）“三线”合一，感受等腰三角形的对称美和统一美

问题5如图4，AD、AE、AF分别是△ABC的中线、角平分线、高，当AD、AE、AF重合时，△ABC应该满足什么条件？如何验证自己的猜想？

以开放的问题，让学生先猜想结论，再操作验证。学生不难发现，三角形的中线、角平分线、高重合时，三角形是等腰三角形，从而充分感受等腰三角形的对称美和统一美。此外，可以进一步追问为什么这时中线、角平分线、高重合，让学生在说理中加深对“三线”概念的理解。

（六）应用性质，感受面積等分的创造美和理性美，挑战适度的困难

问题6请用多种方法把如图5所示的△ABC的面积分成四等份。

追问1如何六等分一块三角形薄饼（厚度忽略不计，面积记为S）？小明同学给出了如下操作：

第一步：如图6，沿边AB、AC上的中线各切一刀，分成四块;

第二步：如图7，再沿边BC上的中线切一刀，分成六块。

请问：小明第一步分成四块后，有没有面积相等的两块？第二步分成的六块面积相等吗？为什么？

学生很容易发现，三角形的中线把三角形的面积分成两等份。那么，如何把三角形的面积分成四等份呢？这个问题有一定的开放性和挑战性，可以让学生独立思考，交流碰撞，聚集众人的智慧，获得多种不同的分法。如图8所示是几种常见的分法。对于多种不同的分法，可以引导学生按照审美原则进行评选。由此，学生可以充分感受到数学的创造美。

在追问中，学生不需要给出把三角形的面积六等分的方法，但是需要对已有的方法进行说理。这个问题具有一定的深刻性和挑战性，能培养学生的逻辑推理能力，让学生感受到数学的理性美。

最后是本节课的回顾反思环节，具体设计省略。

二、教学立意的进一步阐释

（一）挖掘内容元素，让学生体验数学美

数学中的概念、符号、定理、公式、思想、方法等内容都蕴含着美学元素。但是，它们都不是一蹴而就的，需要经历从朦胧到模糊、从模糊到清晰、从清晰到精致的过程，浓缩了数学家集体的智慧。因此，它们的美是内隐和深沉的，不如文学、绘画、音乐等来得直观和具体。初中生由于知识水平、个人阅历和审美能力的限制，很难欣赏和品味数学中蕴含的美。因此，教师要用心深入数学内部，从数学史、数学文化、数学本质、数学思维等角度解读数学内容，挖掘美学元素，并适时、适度地把数学之美融入课堂教学，引导学生欣赏、品味。

本节课，笔者充分解读三角形的高、中线和角平分线蕴含的美学元素，化静为动，让学生寻找线段的特殊状态，发现长度、角度的各种平分情况（垂直的本质是平角的平分），体验数学源于自然的对称（以及简洁）之美。笔者又充分解读重心位置证明过程中的美学元素，联系实际，让学生基于微分思想，自然地发现三角形的重心恰好是三条中线的交点，从而体验数学应用于实际的方法之美。

（二）创设活动情境，让学生发现、创造数学美

数学教学实质上是数学活动的教学。因此，教师要根据学生的认知特点，把数学内容中的美学元素从学术形态转化成教育形态，作为载体，创设层层推进的活动情境，使学生通过自身的数学活动自觉地发现、创造数学美，从而感到惊讶，受到震撼。

本节课，笔者让学生利用画图或折纸的方法得到三角形的三条中线、角平分线、高，甚至三边的垂直平分线。学生惊讶地发现它们都恰好相交于一点，从而强烈地感受到数学的和谐美与统一美。同样地，笔者让学生在作图的过程中，发现垂心、重心和外心居然在同一条直线上，再次惊讶于数学的奇妙。此外，把一个三角形的面积四等分，引出多种分法等活动，则是让学生创造数学美。

（三）在数学美中孕伏适度的挑战，让学生感到数学好玩

除了美，数学的魅力还来自适度的挑战。诚如米兰·昆德拉所说的“麻烦的事情里头，隐藏着真正的乐趣”，有挑战，才好玩，像游戏。陈省身先生倡导“数学好玩”，要在玩中学、在学中玩，才会喜欢、热爱数学，进而自觉地努力去学习数学，甚至享受其中的艰难。因此，教师要设置或孕伏一些具有挑战性的问题，通过明示或暗示，激起学生的好奇和惊讶，引导学生接受挑战，去玩数学。

本节课，学生发现三角形的中线、角平分线和高相交于一点后，必然对为什么相交于一点感到好奇和惊讶;发现三角形的垂心、重心和外心在同一条直线上后，必然对为什么在同一条直线上感到好奇和惊讶。这些都是有挑战性的问题，给学生留下了探索的空间，激发了他们的斗志。此外，把一个三角形的面积四等分，乃至说明把一个三角形的面积六等分的方法是正确的，也都是有挑战性的问题。学生在众多具有美感的分法中，在从一个简单、明显的结论推导出一个复杂、隐蔽的结论的过程中，必然会感觉到数学好玩。

总之，对数学美的追求归根结底是对数学真理的追求，对数学挑战的喜爱归根结底是对生命活动的热爱。当学生被激发出追求美、喜爱挑战的情感时，学好数学自然水到渠成。

参考文献：

[1] 李尚志.从数学中享受快乐[J].数学通报，2004（12）.