对“平面与平面平行的判定”的教学设计反思及改进

孙秀玲

【摘要】笔者近期在进行“平面与平面平行的判定”的课题备课过程中发现，大部分老师在公开课或者教案设计的时候对于判定定理的引出存在一些细节的疏漏或者说缺少必要的解释。本文通过对这些问题进行梳理反思，对教学设计给出了相关建议，供一线老师教学参考。

【关键词】“平面与平面平行的判定”  教学设计  反思  改進

【中图分类号】G42 【文献标识码】A 【文章编号】2095-3089（2020）11-0219-02

一、问题提出

“平面与平面平行的判定”是高中人教版必修2第二章第二节的内容，笔者在观看公开课视频及查阅相关教案后发现，部分老师对于如何从“平面A内的2条平行直线分别平行平面B”的题设巧妙过渡到“平面A内的2条相交直线分别平行平面B”的题设这一细节并未做详细推敲或者缺少必要解释，如果从学生的认知思维出发，肯定会问“A平面内的2条平行直线与B平面平行”不满足要求，那A平面的3条直线，4条直线或者无数条甚至到所有直线都与平面B平行，是否满足判定定理呢？那作为老师，应该在课前就对此处的细节考虑周全，以便使学生更好地接受。另外在进行问题探究的过程中，当提出“A平面内的1条或者2条平行直线与B平面平行”的时候，直接利用长方体或者正方体模型来观察，能否用其他实物来演示？或者让学生实际操作探究得出问题的正确性？当提出“A平面内的2条相交直线与B平面平行”的时候不少老师直接借用正方体或者长方体模型，这样可能会让学生感觉到长方体或者正方体是否太特殊了点，能否用其他方法来证明呢？

二、教案分析

【教材分析】

（1）“两个平面平行的判定定理”是在学习了空间直线的位置关系（包括公理4）、直线与平面的位置关系的基础上进行的，对平行关系而言是对线线平行、线面平行以及面面平行三种位置关系的知识结构进行系统建构的时机。

（2）面面平行的位置关系所具有的性质是研究平面与平面之间的度量关系的转化依据（两个平行平面之间的距离可以转化为线线距、点线距;面面角可以通过面面平行的性质进行灵活转化）。

【教学目标分析】

（1）理解平面与平面平行的判定定理。

（2）运用平面与平面平行的判定定理进行证明，体会面面平行向线面平行转化的思想。

重点是目标（1）、（2）;难点是目标（1）。

【学情分析】

（1）知道面面平行的概念。

（2）掌握线面平行的判定。

（3）运用文字语言、图形语言、符号语言描述定理的基本技能。

【教学过程摘录片段】

摘取2个案例片段，实际感受教师的教学，对问题的提出进一步明朗。

【课堂片段1，师1探究过程】

问题1：如何判定2个平面平行？能用定义判定吗？

问题2：已知两个平面α，β，若？埚l？奂α，l//β，则α//β？

问题3：已知两个平面α，β，若？埚l1，l2？奂α， l1//β， l2//β，则α//β？

问题4：已知两个平面α，β，若？埚l1，l2？奂α，l1与l2相交， l1//β， l2//β，则α//β？

【说明】对于问题1，学生都说不能，因为平面是无限伸展的，对于问题2和问题3，学生通过操作，确认也是错误的，并举出了反例。但师1直接在问题3后将平行改为相交，来得有些突然，对于中低层次的学生来讲，可能会受思维定势的影响，会认为2条直线不行，那3条甚至无数条呢？另外还有一种特殊的情况就是A平面的任何一条直线都与B平面平行，这个也能判定2平面平行，所以师1在此处的处理欠妥。

【课堂片段2，师2探究过程】

师：下图中两个平面平行吗？为什么？你是怎么知道的？

生：平行，因为他们没有交点，直接看出来的。

师：平面是无限延伸的，怎么看到无穷远处呢？下面我们分组讨论，如何找到平面与平面平行的条件;得出结论后由小组代表发言。

生1：作一条直线l，l 垂直α，l 垂直β，则α//β。

师：这个方法很实用，建筑工人盖楼时，确定每层楼与地面平行用的就是这种方法。

生2：如果两个平面α， β没有公共点，那么α内任何一条直线l与β都没有公共点。所以，如果α内任何一条直线l与β都没有公共点，那么α//β。

师：你怎么才能做到任何一条呢？α内一条行不行？α内2条行不行？无数条呢？

【说明】师2利用反证法在正方体中找到反例，比较顺理成章引出定理，但同于上述师1，对于平面A内所有直线都平行与平面B这个特殊情况未加阐述，容易误导学生，使得他们会误认为这种情况也是错误的。

三、教案反思及改进

通过上述2个教学片段，及笔者自身在准备试讲的过程中体会到，教师在进行教学准备需要先进行教学预设，从学生的认知出发，让每个环节能顺利衔接，如将上述2个片段融合起来，将问题串的设定从易到难且全面，不漏掉每个环节，则学生能更好地接受和掌握新知识;在得出判定定理之后再通过变式训练进行巩固。以下是重新编制的教学案例片段：

1.复习回顾

复习1：直线与平面平行的判定方法？

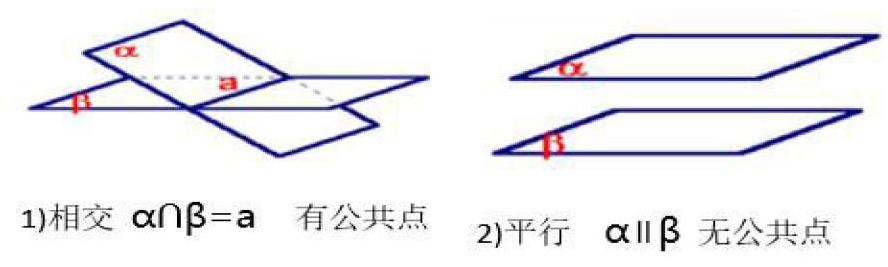
复习2：两个平面的位置关系？

通过实际生活中的例子展示平面与平面的位置关系，紧接着问题3：如何来判定平面平行？同学们回忆下平面与平面平行的定义，得出的结论就是：不可能把其中一个平面内所有直线都取出逐一证明其平行另一平面，引发学生思考。

2.合作探究，得出定理

判定下面2个问题：

问题1：平面α内有一条直线a平行平面β，则α∥β吗？请举例说明。

问题2：平面α内有两条直线a，b平行平面β，则α∥β吗？请举例说明。

问题3：平面α内有无数条直线a，b平行平面β，则α∥β吗？请举例说明。

问题4：平面α内所有直线都平行平面β，则α∥β吗？请举例说明。

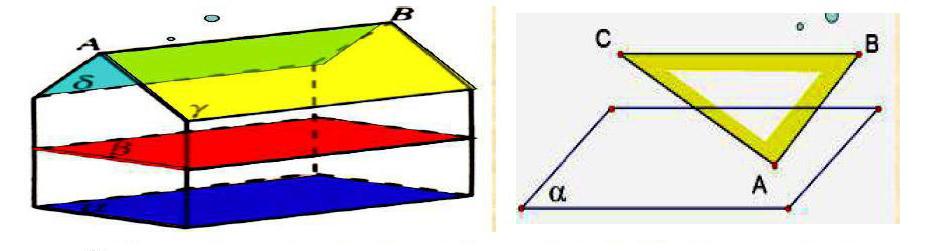
问题5：要证所有直线，不太可行，直线与直线间还有个位置关系，那就是相交，那如果平面α内有2条相交直线a，b平行平面β，则α∥β吗？请先直观感受下。

问题6：动手实操，借用三角板或者书的摆放来看如何让三角板或者书所在的平面平行于桌面？

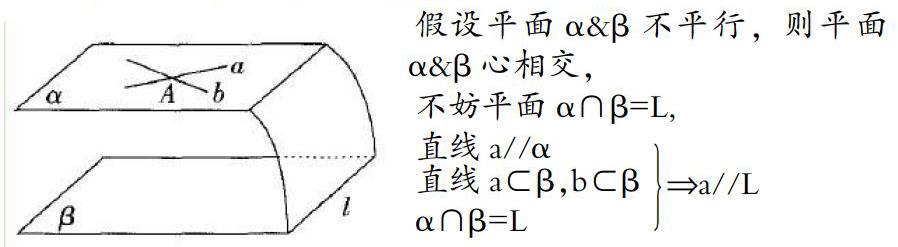
问题7：如果用反证法来看下如何证明？

假设平面α&β不平行，则平面α&β心相交，

不妨平面α∩β=L，

直线a//α

直线a？奂β，b？奂βα∩β=L？圯a//L

同理，b//L，从而a//b，

这与a∩b=P矛盾，所以假设错误，

平面直线α//β。

最后借用正方体模型验证得出判定定理。

3.变式训练，加强巩固。

参考文献：

[1]余建国.“平面与平面平行的判定定理”的教学反思[J].中国数学教育，2016（1-2）.

[2]余其华.证还是不证？《平面与平面平行的判定》教学设计谈起[J].中学数学教学，2018（01）.

[3]李伟.基于学习分类理论的数学规则课设计——以“平面与平面平行的判定”的教学设计为例[J].中小学数学，2015（1-2）.

[4]徐琴.高中数学立体几何教学的几点思考——以“平面与平面平行的判定定理”为例[J].数学教学通讯，2017（06）.