非奇异H-矩阵的一组新判定法

陈 茜, 庹 清

(吉首大学数学与统计学院，湖南吉首 416000)

1 引言

非奇异H-矩阵的应用十分广泛，其判定条件一直是国内外学者研究的热点问题.黄廷祝、干泰彬等国内学者早期根据非奇异H-矩阵的定义和性质，综合利用不等式的放缩技巧，给出了非奇异H-矩阵的一些充分判定条件[1-3]，推广和改进了一些已有的结论[4].刘建州、庹清、谢清明等学者在前人工作的基础上做出了更好的结果[5-7].近年来，以徐仲、陆全等人为主的学者们运用迭代细分的思想，改进和推广了若干重要结果[8-10].

记Mn(C)(Mn(R))为n 阶复(实)矩阵的集合.设A=(aij)∈Mn(C)，记

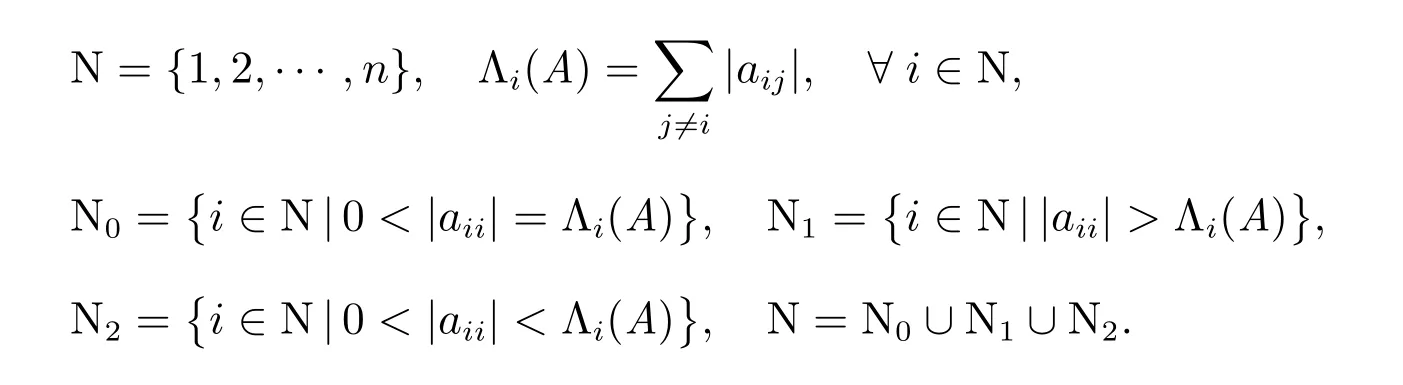
定义1[3]设A = (aij) ∈Mn(C)，若满足|aii| ≥Λi(A)(i ∈N)，则称A 是对角占优矩阵；若满足|aii| ＞Λi(A)(i ∈N)，则称A 是严格对角占优矩阵，记作A ∈D；若存在正对角阵X 使AX ∈D，则称A 为广义严格对角占优矩阵(非奇异H-矩阵)，记作A ∈.

由文献[3]知，若N1= ∅，则A /∈ ˜D；若N0∪N2= ∅，则显然A ∈ ˜D.故我们设N1̸=∅, N0∪N2̸=∅.由于H-矩阵的主对角元均非零，因此，文中所涉及矩阵的对角元均假设为非零.假定矩阵的每一行的非对角线元素的模和为正，本文在不混淆的情况下，简记Λi=Λi(A).

定义2[3]设A=(aij)∈Mn(C)为不可约矩阵，若|aii|≥Λi(A)(i ∈N)，且其中至少有一个严格不等式成立，则A 为不可约对角占优矩阵.

定义3[3]设A = (aij) ∈Mn(C)，若|aii| ≥Λi(A)(i ∈N)，且其中至少有一个严格不等式成立，又对每个等式成立的下标i，都存在非零元素链aij1aj1j2···ajk−1jk̸= 0，使得|ajkjk|＞Λjk(A)，则称A 为具有非零元素链的对角占优矩阵.

引理1[4]设A=(aij)∈Mn(C)为不可约对角占优矩阵，则A ∈˜D.

引理2[4]设A=(aij)∈Mn(C)为具有非零元素链对角占优矩阵，则A ∈˜D.

2003 年，干泰彬、黄廷祝在文献[1]中给出了如下结果：

定理1[1]设A=(aij)∈Mn(C)，若对任i ∈N0∪N2，有

则A 是非奇异H-矩阵.

2004 年，干泰彬、黄廷祝在文献[2]中给出了如下改进结果：

定理2[2]设A=(aij)∈Mn(C)，若

则A 是非奇异H-矩阵.

2008年，庹清、朱砾、刘建州在文献[5]中给出了进一步的改进结果：

定理3[5]设A=(aij)∈Mn(C)，若

其中

则A 是非奇异H-矩阵.

本文在以上工作的基础上，改进文献[5]中的主要结果和文献[1-3]中的部分结果，我们将给出一组判定新条件，并用数值实例说明新条件判定范围更广泛.

2 主要结果

为了叙述方便，引入下列符号：由r, m, δ 的定义，可以得到0 ≤r ＜1, 0 ＜m ＜1, 0 ＜δ ＜1.

定理4设A ∈Mn(C)，若满足

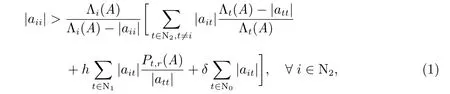
且对任意的i ∈N0，存在t ∈N1∪N2，使得ait̸=0，则A 是非奇异H-矩阵.

证明 由0 ≤r ＜1, 0 ＜m ＜1, 0 ＜δ ＜1，根据r, Pi,r(A)的定义，对任意i ∈N1，有

即Pi,r(A)≤r|aii|, ∀i ∈N1，则有

又由Pi,r(A)的定义，对任意i ∈N1，有

由h 的定义知，对任意i ∈N1，有0 ≤h ＜1，且

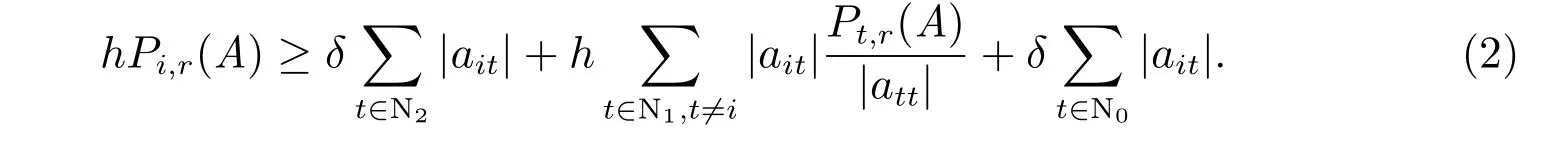
对任意i ∈N2，由(1)式，有

令

从而必有充分小的正数ε，使

构造正对角矩阵D=diag(d1,d2,··· ,dn)，记B=AD=(bij)，其中

对任意i ∈N0，存在t ∈N1∪N2，使得ait̸=0.由0 ＜δ ＜1，对任意t ∈N2，

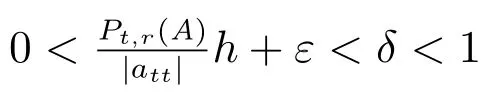
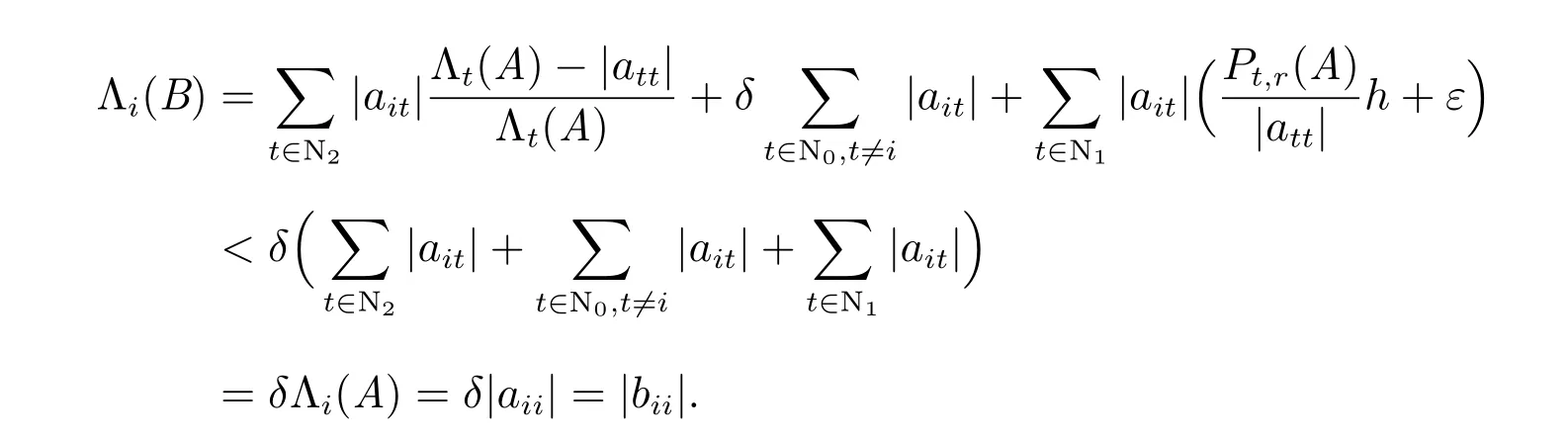
综上所述，|bii|＞Λi(B)(∀i ∈N)，即矩阵B 是严格对角占优矩阵，故矩阵A 是非奇异H-矩阵.

注1在定理4 中，由于对任意的i ∈N1, 0 ≤h ＜1，有

故定理4 的条件包含了文献[5]中定理1 的条件，同时改进了文献[1-3]中定理1 的条件.最后的数值例子也将说明这一点.

定理5设A ∈Mn(C)，A 不可约，若

且(4)中至少有一个以严格不等式成立，则矩阵A 是非奇异H-矩阵.

证明 类似定理4 的证明方法.由于A 是不可约的，故存在任一非空集K ⊂N, ∀i ∈K, j ∈N/K，有|aij|不全为0.

构造正对角矩阵D=diag(d1,d2,··· ,dn)，记B=AD=(bij)，其中

对任意i ∈N2，由(4)式可知，Λi(B)≤|bii|显然成立.对任意i ∈N0，因为对任t ∈N2，

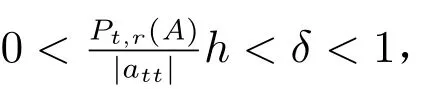
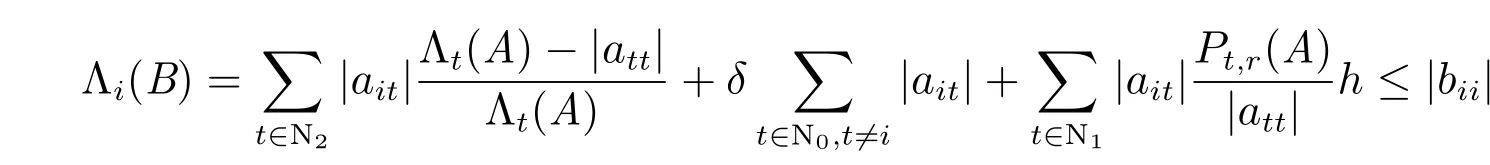
所以|bii| ≥Λi(B), ∀i ∈N.又由(4)中至少有一个以严格不等式成立，即存在一个i0∈N2，使得|bi0i0|＞Λi0(B).

由于矩阵A 不可约，则矩阵B=AD 不可约，由引理1 知，矩阵B 是不可约对角占优矩阵，即B 为非奇异H-矩阵，故矩阵A 是非奇异H-矩阵.

注2定理5 条件包含了文献[5]中定理2 的条件，同时改进了文献[1-3]中定理2 的条件.

类似定理5，利用引理2，有如下结论：

定理6设A ∈Mn(C)，若

且对任意的i ∈N −K，存在非零元素链aii1,ai1i2,···aisi∗，其中i ̸= i1, i1̸= i2,···is̸=i∗, i∗∈K，则A 是非奇异H-矩阵.

3 数值实例

例1

判定矩阵A 是否为非奇异H-矩阵，其中N0= ∅, N1= {3,4}, N2= {1,2}.通过计算可以知道不能用文献[5]中定的理1 判定，同样也不能用文献[1-3]中的定理1 来判定.

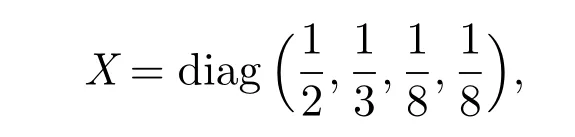
易验证AX ∈D，故矩阵A 确为非奇异H-矩阵.

例2

判定矩阵A 是否为非奇异H-矩阵，其中N0= {1}, N1= {4,5}, N2= {2,3}.通过计算可知不能用文献[5]中的定理1 判定，也不能用文献[1-3]中的定理1 来判定.

易验证AX ∈D，可见矩阵A 确为非奇异H-矩阵.

例3 设

其中

判定矩阵A 是否为非奇异H-矩阵，其中N0=∅, N1={21,··· ,80}, N2={1,··· ,20,81,··· ,100}，利用定理4 可判定矩阵A 是非奇异H-矩阵，即A ∈.其中，取正对角矩阵

X=diag(0.1304I, 0.6400I, 0.5600I, 0.6400I, 0.0909I),

易验证AX ∈D，所以矩阵A 是非奇异H-矩阵.