一类捕食-食饵模型正解的存在唯一性与稳定性
杨梦娜, 李艳玲
(陕西师范大学数学与信息科学学院,西安 710119)
1 引言
具有Holling-III 型功能反应函数的捕食-食饵模型作为一类重要的生物模型,得到了国内外很多学者的关注[1-6].其中文献[1]使用迭代方法和构造相关序列研究了一类具有Holling-III 型反应函数的捕食-食饵模型,得到了正常数平衡解的全局渐近稳定性;文献[2]利用锥上不动点理论和线性稳定性理论研究了一类具有Holling-III 型非线性密度制约的捕食-食饵模型,得到了正解的存在性与稳定性;文献[4]利用分歧理论、隐函数定理以及摄动技巧研究了一类具有非单调生长率且功能反应函数为Holling-III 型的捕食-食饵模型,得到了其正解在一维情形下的存在性及稳定性.本文是在文献[4]的基础上,进一步研究如下的捕食-食饵模型



本文主要利用不动点指标理论和扰动理论研究问题(2)在N 维情形下正解的存在唯一性与稳定性.
2 预备知识
本节首先给出一些基本的定义和引理,其次运用极值原理和上下解方法得到问题(2)正解的先验估计和正解存在的一些必要条件.
如果问题(2)的一个解满足对任意的x ∈Ω, u(x) >0 且v(x) >0,则称(u,v)为问题(2)的一个正解.
设q(x)∈Cα(Ω)(0 <α <1), λ1(q)为如下特征值问题
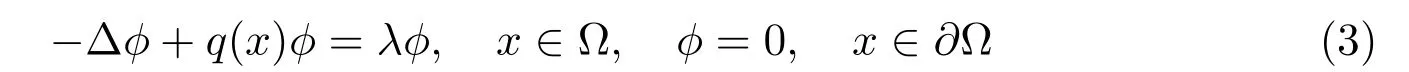
的主特征值.由文献[9]可知,λ1(q(x))连续依赖于q(x),且λ1(q(x))是简单的.另外,λ1(q(x))是关于q(x)的递增函数.为了简单起见,定义λ1(0) = λ1,对应的特征函数记为φ1,且φ1>0, x ∈Ω.
考虑以下非线性边值问题

和

由文献[10]可知,若a ≤λ1,则问题(4)只有平凡解u = 0;若a >λ1,则问题(4)存在唯一正解,记为θa.特别地,θa<a 且连续依赖于a.由文献[4]可知,若α −d >λ1(q(x)),则问题(5)存在唯一正解,记为θα,d(q),并简记θα,d(0) = θα,d.因此,在一定条件下,问题(2)存在半平凡解(˜u,0)及(0,˜v),其中˜u=θa, ˜v =θ1,d.

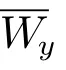
1) 若F′(y)具有α 性质,则indexW(F,y)=0;
2) 若F′(y)没有α 性质,则indexW(F,y)=(−1)β,其中β 是F′(y)的所有大于1 的特征值的代数重数之和.
引理2[11]令q(x) ∈Cα()(0 <α <1),M 为正常数,使得对任意的x ∈, −q(x)+M >0,则以下结论成立:
1) λ1(q(x))<0 ⇒r[(−△+M)−1(−q(x)+M)]>1;
2) λ1(q(x))>0 ⇒r[(−△+M)−1(−q(x)+M)]<1;
3) λ1(q(x))=0 ⇒r[(−△+M)−1(−q(x)+M)]=1;其中r[(−△+M)−1(−q(x)+M)]为算子(−△+M)−1(−q(x)+M)的谱半径.
引理3如果(u,v)为问题(2)的正解,则

证明 假设(u,v)为问题(2)的正解,从关于u 的方程可以得到

因此˜u 可以作为下述问题


令z =cu+mv,结合u 和v 的方程,则z 满足

由极大值原理可知

又由于z =cu+mv,从而

引理4如果问题(2)存在正解,则

证明 设(u,v)是问题(2)的正解,则
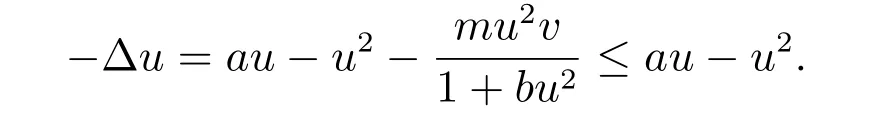
对上式两端同时乘以u,再在Ω 上积分,运用格林公式,则

又由Poincar´e 不等式可知

从而a >λ1.
从v 的方程中,可以得到
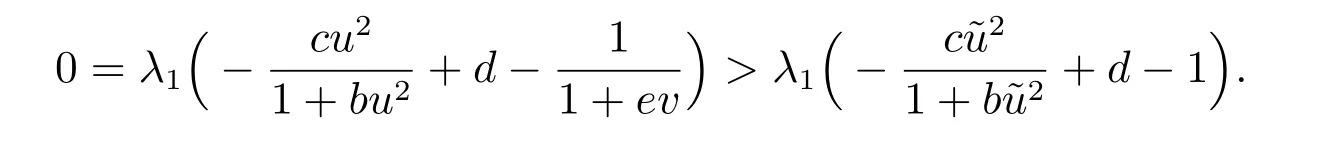
因此

3 正解的存在性
本节主要利用不动点指标理论[2,12]研究问题(2)正解的存在性.为了计算不动点指标,引入以下记号:
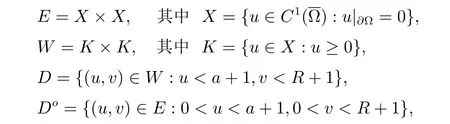
则通过计算得到:
取M 充分大,使得(u,v)∈D 时

定义算子F: E →E:
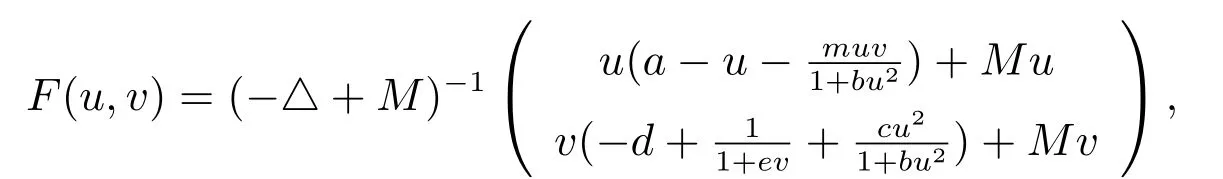
则F :D →W 是紧算子,则问题(2)有解等价于算子方程F(u,v)=(u,v)有解.
对于任意的t ∈[0,1],定义
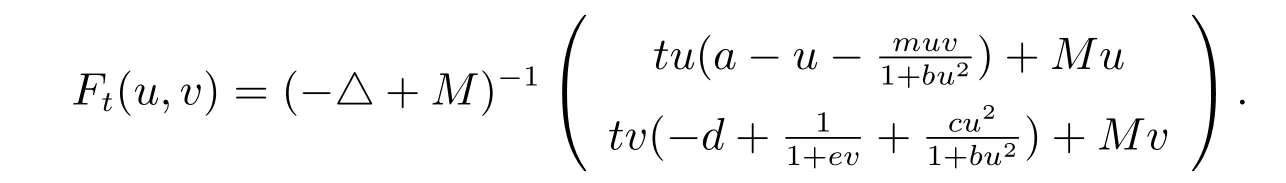
引理5假设a >λ1,则有:
1) degW(I −F,D)=1;
2) 若−d+1 ̸=λ1,则indexW(F,(0,0))=0;


证明 1) 由引理3 知,F 在∂D 上没有不动点,因此degW(I −F,D)有意义,对于任意的t ∈[0,1],Ft的不动点为下述方程的解

则对于任意的t ∈[0,1],Ft的不动点满足u ≤a, v ≤R.因此Ft的不动点一定落在D 内,再由度的同轮不变性知,degW(I −Ft,D)不依赖于t,于是
degW(I −F,D)=degW(I −F0,D)=degW(I −Ft,D).
当t=0 时,问题(7)只有平凡解(0,0),所以degW(I−F0,D)=indexW(F0,(0,0)).注意到

记

由引理1 知,indexW(F0,(0,0))=1,因此degW(I −F,D)=1.
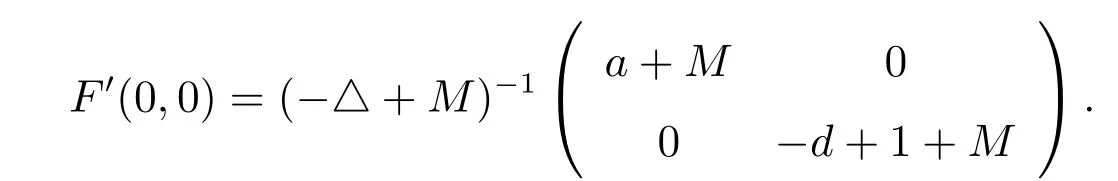
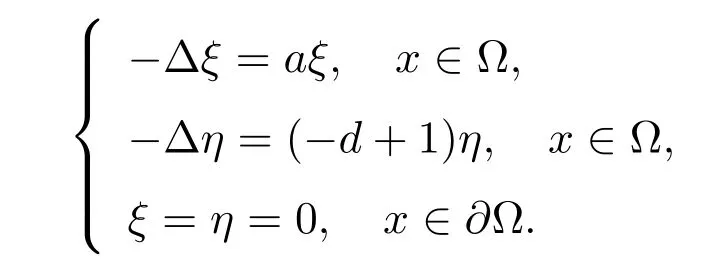
如果ξ >0,则a = λ1,这与已知相矛盾.因此ξ ≡0,同理可证η ≡0.从而I −F′(0,0)在(0,0)上可逆.

又由于a >λ1,则同时ra为算子(−△+M)−1(a+M)的主特征值,对应的特征函数φ >0,取t0= r−1a,则0 <t0<1,并且(I −t0F′(0,0))(φ,0)=(0,0)∈S(0,0),因此F′(0,0)具有α 性质,从而由引理1 知,indexW(F,(0,0))=0.
3) 通过计算得到


若η ̸≡0,则由η ∈K 知
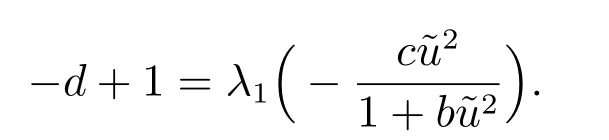

记

由于

从而由引理2 可知,r(A) >1 且是算子A 的主特征值,相应的特征函数φ >0,取t0=r−1(A),则0 <t0<1, (0,φ)∈(u˜,0)S(u˜,0),并且
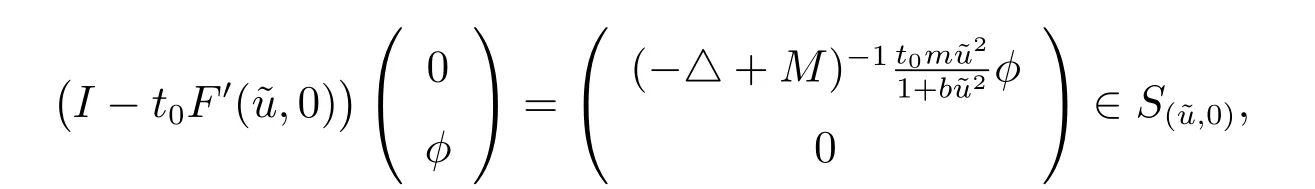
因此F′(u˜,0)在W(u˜,0)上具有α 性质,从而由引理1 知,indexW(F,(u˜,0))=0.
4) 由上节可知,当

时,I −F′(u˜,0)在(u˜,0)上可逆.由于
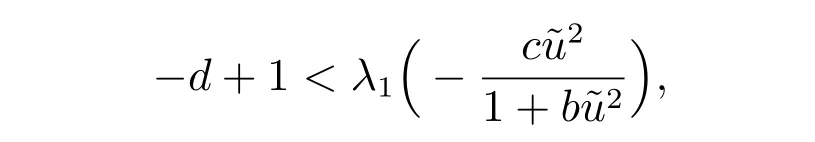
从而r(A) <1.假设F′(u˜,0)在(u˜,0)上具有α 性质,则存在0 <t <1, (φ1,φ2) ∈(u˜,0)S(u˜,0),使得
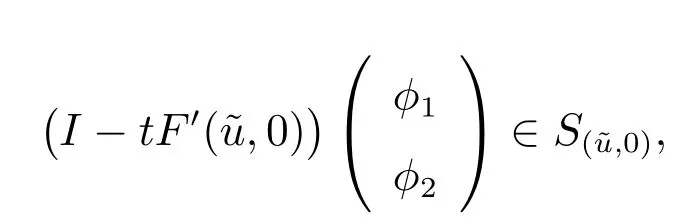
于是

又由于φ2∈K{0}.从而为算子A 的一个特征值,这与r(A) <1 相矛盾.因此F′(u˜,0)在W(u˜,0)上不具有α 性质,根据引理1 可知,indexW(F,(u˜,0)) = (−1)β,其中β 是F′(u˜,0)的所有大于1 的特征值的代数重数之和.

即

如果η ̸≡0,则

从而矛盾,因此η ≡0.
若ξ ̸≡0,则

从而矛盾.因此F′(˜u,0)没有比1 大的特征值.于是根据引理1 得indexW(F,(˜u,0))=1.
类似引理5,我们可以证明如下结论:
引理6设−d+1 >λ1,则:
1) 若a >λ1时,则indexW(F,(0,˜v))=0;
2) 若a <λ1时,则indexW(F,(0,˜v))=1.
从而由引理5 和引理6,以及度的可加性得到问题(2)正解的存在性定理.
定理11) 如果−d+1 >λ1, a >λ1时,则问题(2)除(0,0), (˜u,0), (0,˜v)之外,至少还有一个正解;
2) 如果−d+1 <λ1,则问题(2)存在正解当且仅当

证明 1) 根据引理6 和引理7 可以得到
1=degW(I −F,D)=indexW(F,(0,0))+indexW(F,(˜u,0))+indexW(F,(0,˜v))=0,从而矛盾,因此问题(2)至少还有一个正解.


从而矛盾,因此问题(2)至少有一个正解.

4 正解的唯一性与稳定性
本节主要运用度的可加性质和线性算子的扰动技巧[14-16]来讨论当参数m 充分小时,问题(2)正解的唯一性与稳定性.
首先考虑下述方程


引理7设

则当m >0 且趋于0 时,问题(2)的任意正解都是非退化且线性稳定的.
证明 采用反证法来证明.假设存在mi→0,使得问题(2)在m = mi时的正解(ui,vi)是退化的或者线性不稳定的,则存在(ξi,ηi)̸≡(0,0),使得如下线性化问题的特征值µi满足Re(µi)≤0,不妨设‖ξi‖2+‖ηi‖2=1.

显然,当mi→0 时,(ui,vi) →(˜u,v∗).记¯ξi和¯ηi分别是ξi和ηi的共轭算子,对(9)式的第一个方程乘以¯ξi,第二个方程乘以¯ηi,然后在Ω 上积分,最后两者相加得到
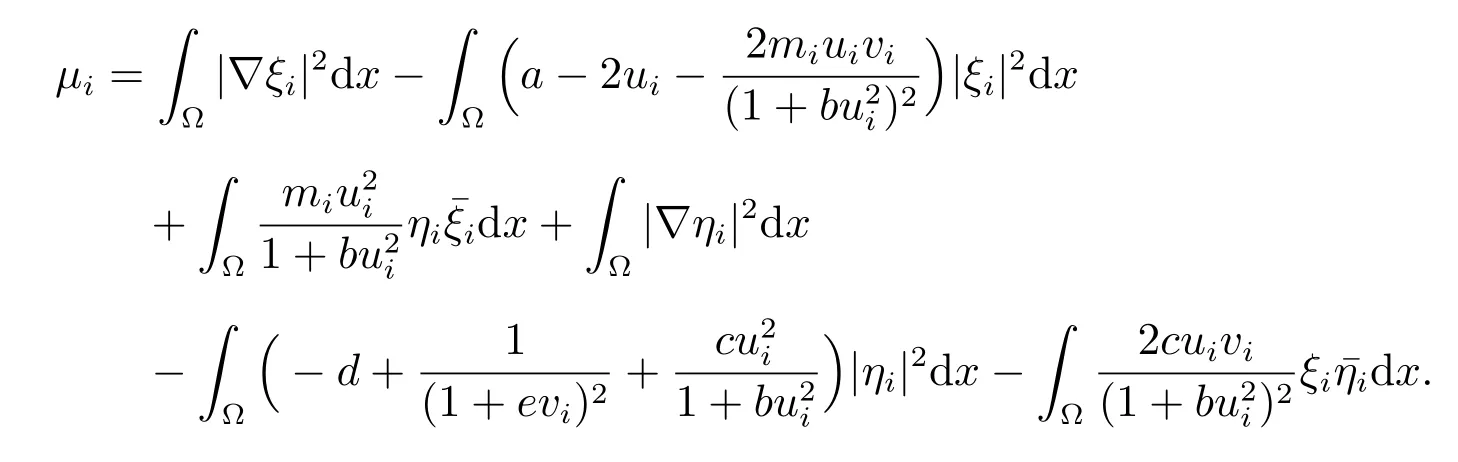
由引理3 知,ui和vi都有界,所以Re(µi)和Im(µi)有界,因此µi有界.可设µi→µ,则Re(µ)≤0.又由Lp估计和Sobolev 嵌入定理可得,ξi和ηi有界,设ξi→ξ, ηi→η.
再对(9)式两端关于i 取极限,得到

若ξ ̸≡0,则算子−△−(a −2˜u)I 的特征值全大于0,因此µ ≥λ1(−a+2˜u) >0,从而与Re(µ)≤0 相矛盾,因此ξ ≡0.
若η ̸≡0,将ξ =0 代入(10)式中第二个方程,则

从而与Re(µ)≤0 相矛盾,因此η ≡0.
所以问题(9)的所有特征值的实部都大于0,这意味着问题(2)的正解是非退化的且线性稳定的.
定理2设

则当m >0 且充分小时,问题(2)有唯一正解,而且是非退化和线性稳定的.
证明 由定理1 和引理7 可知问题(2)存在正解,而且是非退化和线性稳定的,故只需要证明正解的唯一性即可.首先容易验证平凡解和半平凡解都远离正解,再根据紧性理论可知问题(2)至多有有限个正解,记为{(ui,vi) : i = 1,2,··· ,l}.又由引理7 可知,indexW(F,(ui,vi))=1.结合度的可加性及引理6 可得

因此问题(2)只有一个正解,而且是非退化和线性稳定的.
5 数值模拟
这节主要讨论系统(1)对应的一维空间的情形,即

利用Matlab 工具做数值模拟,根据直观图像来验证前面研究得到的理论结果,通过计算可得λ1=.
首先,根据定理1 的条件进行数值模拟,参数取值分别为a = 0.65, b = 1, c =1, d = 0.4, e = 1.25 和m = 0.5.图1 验证了系统(1)在一维情形下正解的存在性,这与定理1 的结论一致,这说明两物种在定理1 的条件下,食饵和捕食者可以共存.并且随着时间t 的增大,可以看出两物种趋于稳定.

图1: 系统(11)的正解(u(x,t),v(x,t))的模拟图,其中图(a)和图(b)分别为正解(u(x,t),v(x,t))的模拟图;图(c)为正解(u(x,t),v(x,t))在T =100 时刻的剖面图;图(d)为任意时刻正解(u(x,t),v(x,t))在(0,2π)上的L1 范数
其次,图2 分别验证了当食饵种群的生长率充分小时,或者捕食者种群的死亡率充分大时,食饵和捕食者不能共存;除此以外,当食饵种群的生长率充分小且捕食者种群的死亡率充分大时,食饵和捕食者也不能共存,这些符合引理4 的结论.
下面给出一个二维空间的例子,验证定理1 的结论.
这里取a=0.65, b=1, c=1, d=0.4, e=1.25, m=0.5 和t=4,从图3 中可以看出,系统(12)的正平衡态解的存在,这说明两物种可以共存.从图4 可以看出,随着时间t 的增大,两物种趋于稳定.

图3: 系统(12)在t=4 时刻(u(x,y,t),v(x,y,t))的模拟图,其中图(a)和图(b)分别为正解(u(x,y,t),v(x,y,t))的投影图;图(c)和图(d)分别为正解(u(x,y,t),v(x,y,t))的模拟图
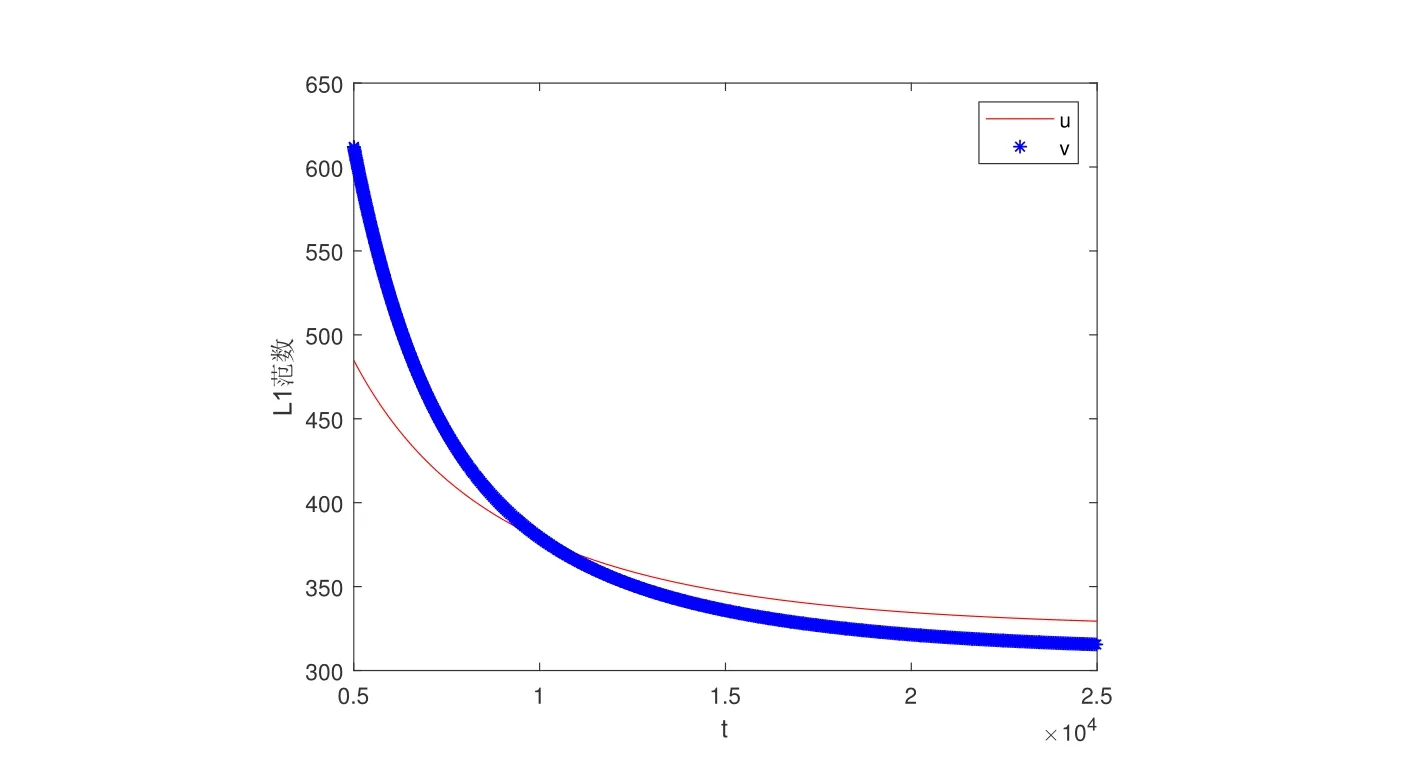
图4: 系统(12)的正解(u(x,y,t),v(x,y,t))在(0,2π)×(0,2π)上的L1 范数

