关于一些特殊图上的强罗马控制数的研究
徐加雪, 王志平
(大连海事大学理学院,大连 116000)
1 引言
对本文使用的符号和术语进行说明.图G 是由顶点集合V(G)和边集合E(G)构成的一个简单图.n = |V(G)|表示图G 的阶数,|E(G)|表示图G 的边数.对于图中的每一个顶点v ∈V(G),它的开邻域和闭邻域分别用N(v) = {u ∈V(G)|uv ∈E(G)}和N[v] =N(v)∪{v}对应表示.d(v) = |N(v)|表示顶点v 的度.f 代表定义在顶点集合V(G)上的函数.f : V(G) →{0,1,2}即表示图中任意的顶点v ∈V(G), f(v) = 0 或1 或2.∆=∆(G)和δ =δ(G)分别表示图G 的最大度和最小度.
图论起源于十八世纪,是一个有着丰富历史背景和实用价值的学科.它是由日常生活中的游戏激发产生的,至今已经有两百多年的发展历史.上个世纪中期,Clande Berge 学者根据国际象棋问题首先提出了图的“控制数”的概念.受Berge 学者的启示,Oystein Ore 学者正式提出了控制数以及相关方面的术语并延续至今.基于不同的实际应用背景以及历史背景,图的控制数衍生出许多新的控制参数,例如弱控制数、独立控制数、距离控制数、符号边控制、罗马控制数等,控制数的种类不断增加.
Stewart 在文献[1]中讲述了公元四世纪时罗马帝国的君主保卫国家的故事.我们把整个罗马帝国视为一个图,令图中的点表示罗马帝国中的每个地区,边表示两个地区相邻.没有军队驻扎的地区称为不安全的地区,反之则称其为安全的地区.军队需要驻扎在不同的地区守护国家的领土安全.安全系数最高的方案是在罗马帝国内的每一个地区都驻扎一支军队.若国家长期处于和平时期,这种防御方案便会造成军队资源的浪费.君主希望在罗马帝国内的每个地区驻扎数量较少的军队,同时能够维持国家的领土完整与安全,于是颁布了一条法令:从一个安全的地区派遣军队去往一个不安全的地区后,使安全的地区转变为不安全地区的情况不可以存在.根据君主的命令可知,只有至少驻扎两个军队的安全地区才能够往相邻的不安全的地区派遣军队,这样既能够保证安全地区在派遣军队之后仍是安全的地区,相邻的不安全的地区接收派遣的军队后也转变为安全地区.在总结已有经验的基础上,1999 年,Stewart 首次提出了罗马控制概念[1].Cockayne 等学者[2]受保卫罗马帝国的历史故事的启发,正式给出了图G 的顶点集合上的罗马控制函数的定义,如下所示:

实际生活中,敌人更倾向于攻击薄弱的地区.当罗马帝国的地区面临敌人的多重攻击时,驻扎两个军队的安全地区,无法保护数量超过三个以上的不安全的邻居,此时罗马帝国很容易失守而落入敌人手中.于是Alvarezruiz 等学者[17]提出一种更符合实际情况的防御新策略,并且定义了图G 的强罗马控制函数,具体地,

是一个定义在图G 的顶点集合V(G)上的函数,若每一个顶点v ∈B0至少存在一个邻结点w ∈B2,且邻结点w 满足

其中


图1 和图2 分别给出了图G 上的罗马控制函数和强罗马控制函数.一次大地震过后往往会伴随着许多余震的发生,数量有限的军队需要驻扎在灾区,随时准备营救受灾群众.假设村庄用图中的点表示,村庄之间的路用图中的边表示.图上的数字表示该村庄中驻扎军队的数量.当面临多个村庄都需要营救时,图1 中的军队不能够及时营救它周围所有受灾的村庄,但图2 中的军队至少能够及时营救一半以上没有军队驻扎的村庄,大大减少生命财产损失.
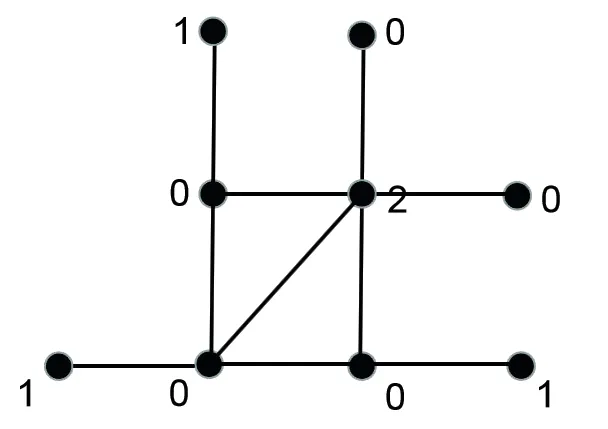
图1: 图G 的罗马控制函数
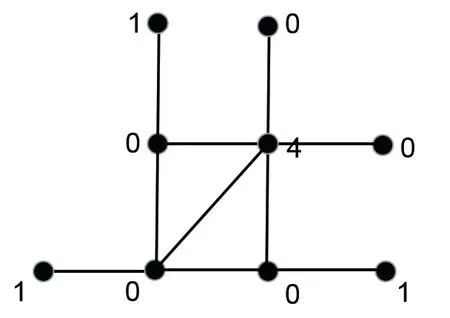
图2: 图G 的强罗马控制函数
人们往往希望利用一个多项式时间算法来求出所有图上的控制数的精确值,但已有结论指出一般图的控制问题是一个NP-完备问题,因此探究出图的控制数或者控制数较好的上下界具有重大的理论意义.Alvarezruiz 等学者在文献[17]中提出了一个开放性问题:所有阶为n ≥3 的连通图是否都有γStR(G)≤成立.为了验证问题的正确性,本文应用数学归纳法和分类讨论方法,深入地讨论了图的强罗马控制数与阶数的关系,得到了风车图、完全二部图、完全图的刺图等特殊图上的强罗马控制数均不大于其阶数的七分之六,从而进一步说明了问题的正确性.
2 主要结论与证明
定理1若G 是一个阶为n ≥3,最大度为∆=n −1 的图,则γStR(G)≤.
证明 假设图G 中的顶点v ∈V(G)的度为d(v) = ∆= n −1.在图G 的顶点集V(G)上定义一个函数f :V(G)→{0,1,··· ,+1},令f(v)=+1,而对任意的顶点x ∈N(v),都有f(x) = 0.显然,函数f 是图G 的顶点集V(G)上一个强罗马控制函数,因此

同理可知,风车图、扇图、凤梨图等都是阶为n ≥3 且最大度为∆=n −1 的图,所以这些特殊图均满足γStR(G)≤.
若图G 的顶点集合V(G)划分为两个顶点子集V1、V2,且满足在同一顶点子集的任意两个顶点之间不存在边且图中的每条边连接不同顶点子集中的顶点,则称图G 是一个二部图. 若图G 是一个二部图,且顶点子集V1中的任意一个顶点均邻接顶点子集V2中所有的顶点,此时则称图G 为完全二部图,如图3 所示.

图3: 完全二部图
定理2若图G 是一个阶为n ≥3 的完全二部图,则γStR(G)≤.
证明 令|V1|=p, |V2|=q 且p ≥q.根据假设可知∆=p 和n=p+q.下面分4 种情形来讨论.
情形1n=3.
显然有p=2, q =1 且∆=2.根据定理1 可知γStR(G)≤成立.
情形2n=4.


情形2.2 当p = 3, q = 1 时,则∆= 3 = n −1,由定理1 可知γStR(G) ≤成立.
情形3n=5.
情形3.1 当p = 3, q = 2 时,则∆= 3.假设顶点v ∈V2是图G 中度数最大的顶点,即d(v) = ∆(G).在图G 的顶点集合V(G)上定义一个函数f : V(G) →{0,1,··· ,+ 1},令f(v) =+ 1,而对所有与顶点v 邻接的顶点x ∈N(v),都有f(x) = 0,剩余结点f(w) = 1.显然,函数f 是图G 的顶点集合V(G)上的一个强罗马控制函数,因此有
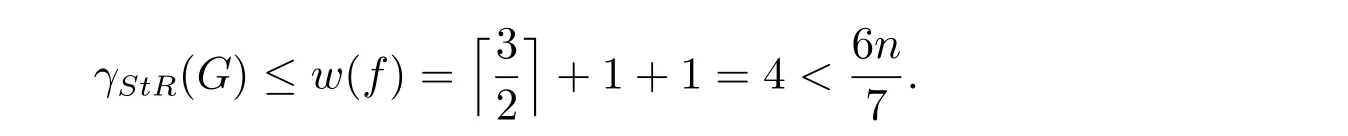
情形3.2 当p = 4, q = 1,此时∆= 4 = n −1.根据定理1 可知γStR(G) ≤成立.
情形4n ≥6.
在图G 的顶点集合V(G)上定义一个函数f :V(G)→{0,1,··· ,+1},令

其中v1∈V1, v2∈V2,剩余结点f(w) = 0.函数f 是图G 顶点集合V(G)上的一个强罗马控制函数,因此有
假设Kz是一个z 阶完全图,a1,a2,··· ,az是正整数且a1≥a2≥···≥az≥1.通过在完全图的每个顶点处分别添加a1,a2,··· ,az个悬挂边可得到完全图的刺图,记做.我们对图中的结点进行标记,图4 展示了完全图K3的刺图的顶点标记规则.
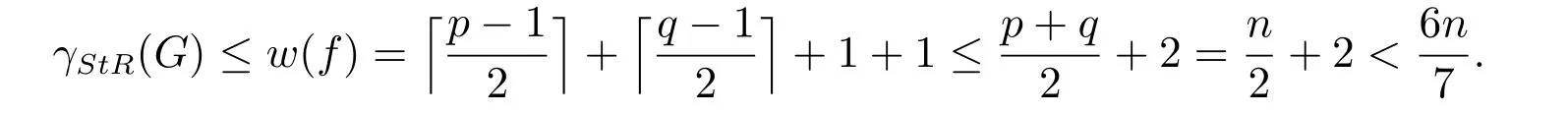

图4: 完全图K3 的刺图
定理3若是一个阶n ≥3 的完全图Kz的刺图,则γStR()≤.
情形1a1=a2=···=az=1.
在这种情形下,图K∗z的阶和最大度分别对应为n = 2z 和∆= z.在图的顶点集合V()上定义一个函数f :V()→{0,1,··· ,+1},选取图中任意一个非叶子顶点v ∈V(K),令f(v) =+1,而对所有与顶点v 相邻接的顶点x ∈N(v),有f(x) = 0,使得剩余结点均满足f(w) = 1.根据强罗马控制函数函数的定义可知,函数f 是图的顶点集合V()上的一个强罗马控制函数,因此有

情形2ai≥2,其中i=1,2,··· ,z.

情形3a1=a2=···=ak=2, ak+1=···=az=1,其中1 ≤k ≤z −1.
假设顶点v1邻接两个悬挂边.在图K∗z的顶点集合V(K∗z)上定义一个函数f :V() →{0,1,··· ,+ 1},令f(v1) =+ 1,而对所有与顶点v1相邻接的顶点x ∈N(v1),均有f(x) = 0,其他剩余结点f(w) = 1.显而易见,f 是图K∗z的一个强罗马控制函数,因此有

情形4a1≥3, a2≥3, ··· , ak≥3, ak+1=···=az=1,其中2 ≤k ≤z −1.
情形4.1 当2 ≤k ≤3 时,在图的顶点集合V()上定义一个函数f :V()→{0,1,··· ,+1},令f(v1)=+1,而对所有与顶点v1相邻接的顶点x ∈N(v1),均有f(x) = 0,剩余结点f(w) = 1.函数f 是图顶点集合V()上的一个强罗马控制函数,因此有
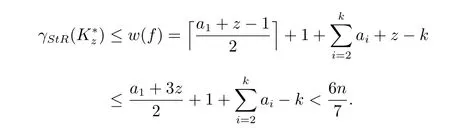
因为
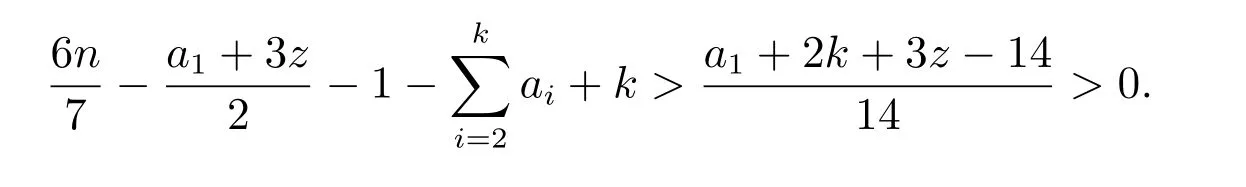
情形4.2 当4 ≤k ≤z −1 时,在图Kz∗的顶点集合V(Kz∗)上定义一个函数f :V()→{0,1,··· ,+1},令

对所有x ∈N(v1)∪N(v2)∪···∪N(vk)−{v1,v2,··· ,vk},均有f(x)=0,其他剩余结点f(w)=1.显然,函数f 是图K∗z顶点集合V(K∗z)上的一个强罗马控制函数,因此有

因为