非高斯噪声激励下非线性漂移Fokker-Planck 方程的非稳态解及其应用
姚 婷, 郭永峰, 樊顺厚, 魏 芳
(天津工业大学数学科学学院,天津 300387)
1 引言
人们通常会把噪声看作是系统和日常生活中的干扰因子和消极因素,因为噪声的存在可能会影响系统的正常运转、干扰信息的采集和对系统的观察.但是随着近年来对随机力研究的不断深入和成熟,使得人们对噪声产生了颠覆性的认识;在一定的非线性条件下,噪声不仅不会对系统产生消极影响,还会产生积极影响,甚至对非线性系统的动力学行为还能起到本质的改变[1-4].噪声根据统计性质可分为高斯噪声和非高斯噪声,对于高斯噪声的研究已经形成了一套比较完整的研究方法和理论体系[1-4].然而对于非高斯噪声的研究却没有高斯噪声那样成熟,由于非高斯噪声不再是马尔科夫过程,因此当非线性系统中含有非高斯噪声时,其理论计算不易处理,但非高斯噪声也不能被忽略,有时它对系统本身有着不可替代的作用.
文献[5-14]对非高斯噪声激励的一系列非线性系统的动力学行为进行了研究.例如,许勇等[9,10]研究了非高斯噪声驱动下一维双稳系统的逻辑操作问题.康艳梅等[11]探讨了一类由非高斯噪声激励的转录调控系统的平均首次穿越时间和随机共振相关问题.张静静和靳艳飞[12]利用路径积分法和两态模型理论,研究了非高斯噪声激励下FitzHugh-Nagumo 神经元系统的随机共振等动力学行为.文献[13]研究了非高斯噪声驱动下分段非线性双稳系统的平均首次穿越时间,并讨论了非高斯噪声和高斯噪声对平均首次穿越时间的影响.与此同时,现有大部分的文献都是基于非线性随机系统Fokker-Planck(FPK)方程的定态解进行研究[8-14],其主要原因是定态解便于计算且能反映系统的长时间行为,然而事实上,随机系统还有许多性质是由非定态解的演化过程所决定的,因此研究随机系统FPK 方程的非定态解是极为必要的.其中,文献[3,4,14-17]讨论了弱噪声极限下非线性非势系统的FPK 方程的非定态解的计算问题.但上述研究主要针对的是高斯噪声,对于非高斯噪声和高斯噪声共同作用下一般非线性随机系统FPK 方程的非定态解的推导还尚未见到.
本文主要研究非高斯噪声和高斯白噪声共同驱动下的非线性漂移FPK 方程的非稳态解问题,我们应用路径分析法和空间扩维法对所研究的系统进行等效变换,同时为了研究系统在不稳定点附近的演化行为,进一步应用格林函数的Ω 展开理论在初始时区域进行线性近似,将二维非线性非细致平衡系统转化为二维奥恩斯坦-乌伦贝克过程来讨论,并在此基础上运用本征值本征矢理论近似得到了一般朗之万方程所对应的近似非稳态解,最后将此研究结果应用到描述产品产量增长的Logistic 系统模型中.
2 非高斯噪声驱动的一般非线性动力学系统FPK 方程的非稳态解
考虑受非高斯噪声和高斯白噪声共同驱动的一维非线性动力学系统,其一般形式的随机微分方程可以表示为[3,4,14,15]
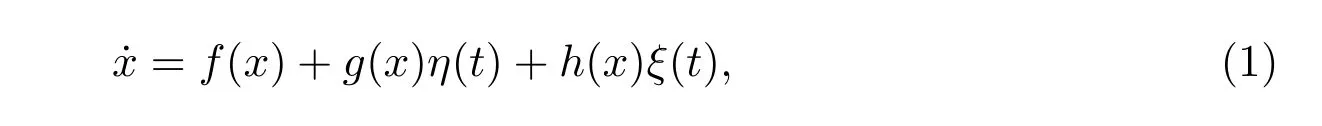
其中f(x)为x 的非线性函数,g(x)和h(x)为x 的函数,η(t)为非高斯噪声,其统计性质如下[5-13]

这里
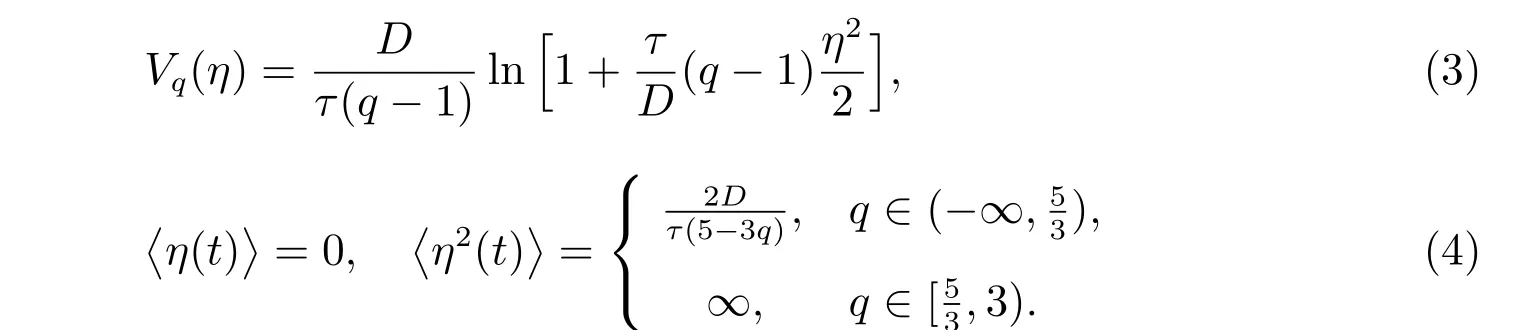
参数q 表示非高斯噪声η(t)偏离高斯分布的程度,显然q ̸= 1(若q = 1,则η(t)不再是非高斯噪声,变为了自相关时间为τ,噪声强度为D 的高斯色噪声),ζ(t)和ξ(t)分别为不相关的高斯白噪声,其统计性质为

D 和Q 分别为ζ(t)和ξ(t)的噪声强度.
引理1当|q −1|<<1 时,对(2)式应用路径积分法可得[5-13]
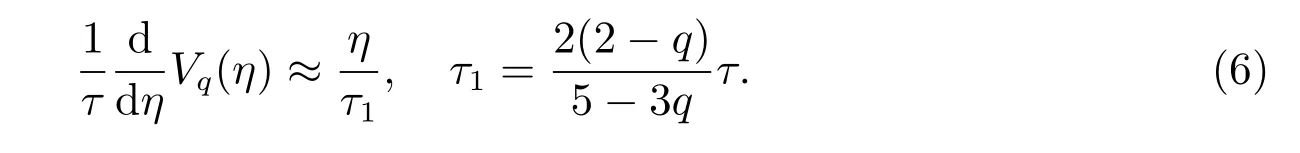
且将(6)式代入(2)式后,非高斯噪声η(t)可以表示为
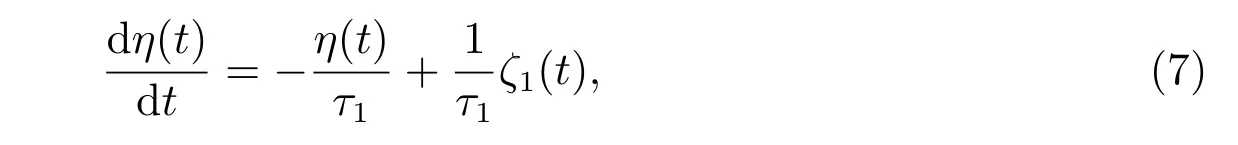
其中ζ1(t)为高斯白噪声,其统计性质为

这里

引理1可将非高斯噪声η(t)近似转化为有效自相关时间为τ1,有效噪声强度为D1的高斯色噪声.由于η(t)中的有限关联时间τ1形成了对历史的记忆,所以这一过程不再为马尔科夫型.为便于研究,在引理1 的基础上,通过增加空间维数将系统(1)等效地改写为

接着对于上述系统(10),用变量z 代换x,可以把乘性白噪声ξ(t)转化为加性白噪声的形式
其中

则系统(11)的二维FPK 方程为
利用初始变量可将上式进一步标记为
此时,方程(13)所对应的确定性方程为
假设方程(14)具有一个不稳定点(xu,0)和一个稳定点(xs,0),由于上述系统不满足细致平衡条件[φ(x)+ψ(x)y] =(−y),为了能够研究该系统在不稳定区域附近的演化行为,根据文献[3,4,14-17]应用格林函数的Ω 展开理论在初始时区域将该二维非线性系统转化为线性系统来讨论.
引理2[3,4,14-17]对确定性系统(14)在不稳定点(xu,0)处进行线性化,并忽略掉高阶项可以得到

其中k1= φ′(xu) >0, k2= ψ(xu), k3= −xuφ′(xu),且线性化后(15)式所对应的二维FPK 方程为
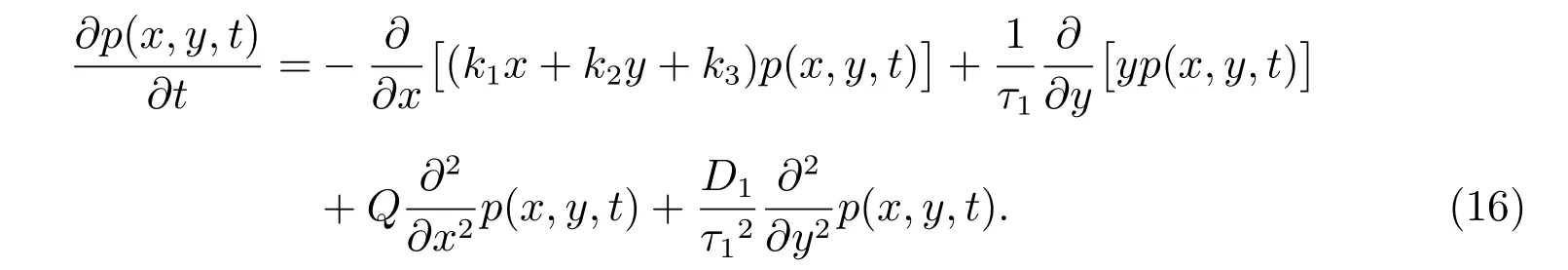
显然(16)式是具有线性漂移力和常系数扩散项的二维奥恩斯坦-乌伦贝克过程.此时线性化系统(16)的初始分布函数为
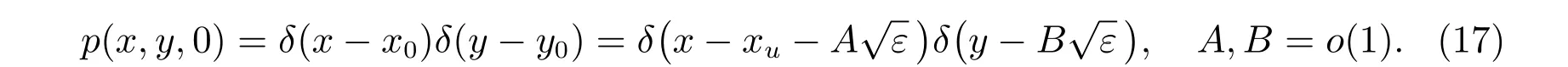
对(16)式作傅里叶变换可以得到[3,4,14-17]

把(18)式带入到方程(16),可以推得
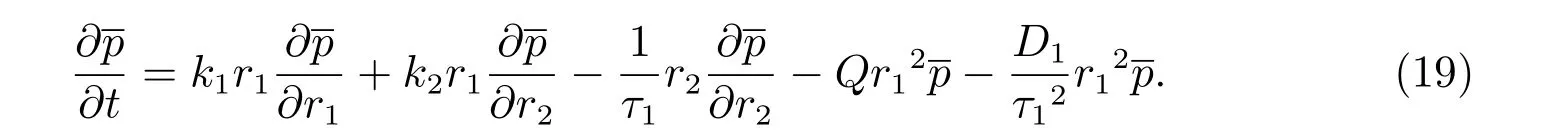
定理1在方程(19)中,若(r1,r2,t)满足初始条件
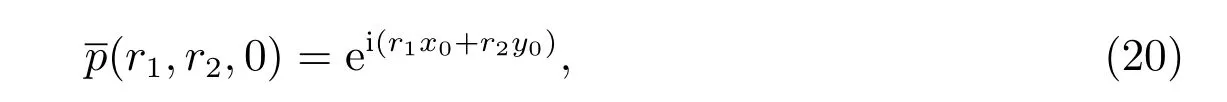
则方程(19)的解是存在的,且根据(18)式亦可得到系统FPK 方程的非稳态解.
证明 我们假设方程(19)的解具有下面的高斯形式[3,4,14-17]

为了满足(20)式所给定的初始条件,显然有

把(21)式代入到(19)式,并比较等式两边r1, r2的次数,可得到下面的微分方程组
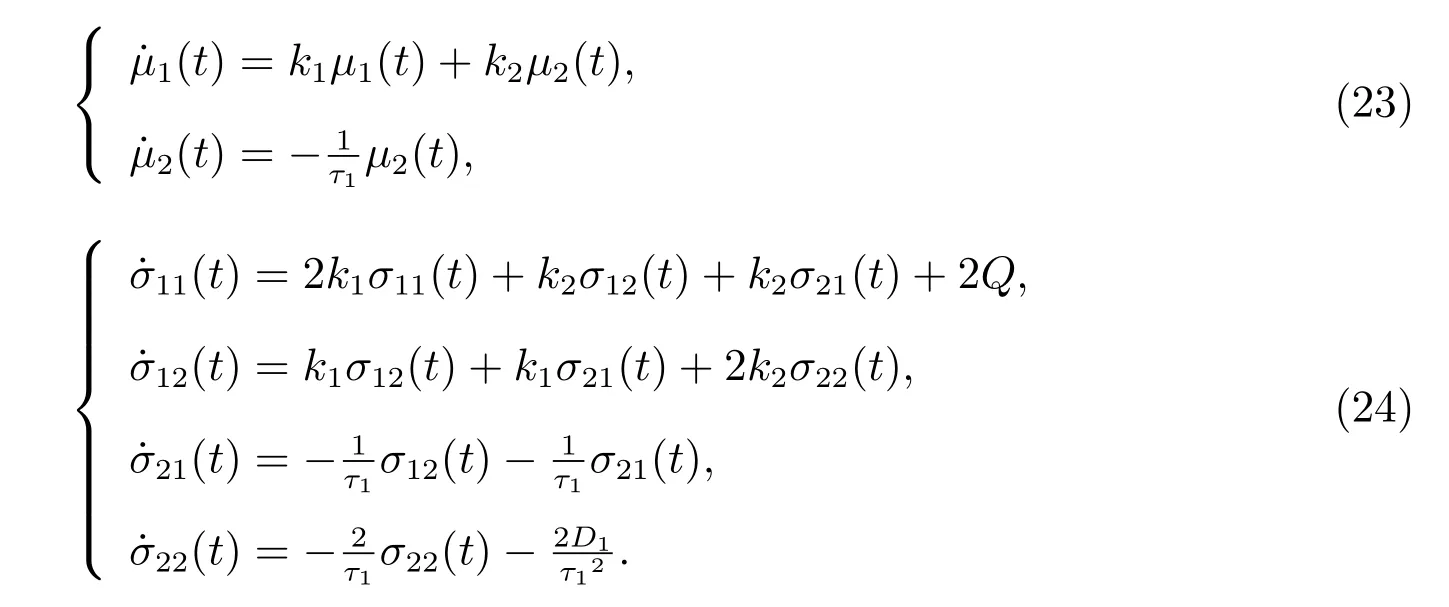
为了能求出方程组(23)和方程组(24)的解,把方程组(23)改写为
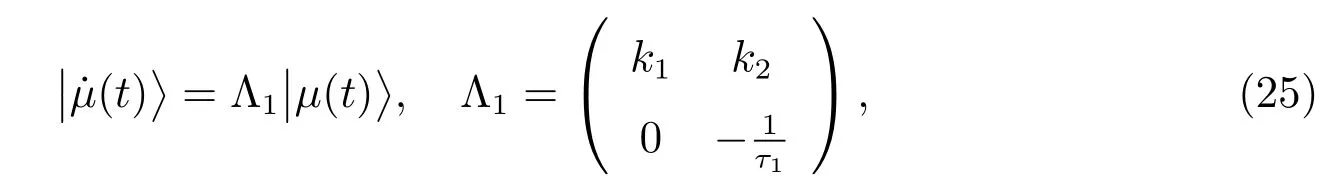
这里Λ1为线性算子,其本征值为
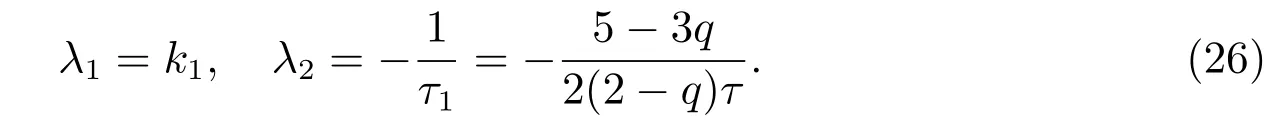
通过进一步求解可得到本征值λ1, λ2对应的本征矢为

将算子Λ1改写为双正交基的形式

根据已有初始条件

方程(23)的解可直接写为
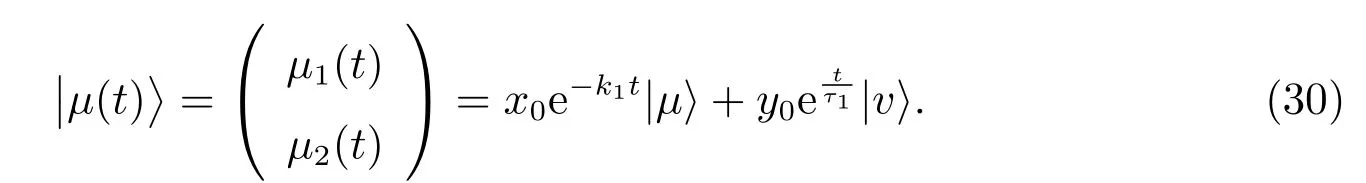
通过计算求得方程(24)式的解为

将(30),(31)式代入(21)式,即可得到方程(19)的解.接着将方程(19)的解带入(18)式,便可以得到系统的非稳态解p(x,y,t)为

将上式关于变量y 积分,可得到宏观变量x 的归一化含时解

其中N 为归一化常数.
3 非高斯噪声驱动的Logistic 系统的非稳态分析及其应用
接下来,可将上述结论应用到Logistic 系统模型[18-20],该模型不仅可以用来描述单一种群的繁殖问题,也可以用来分析产品的产量增长变化现象,这里我们以产品产量增长率满足的Logistic 模型为基础,并且考虑到产品自身的使用寿命和系统内部存在的随机因素(如产品改良升级等)及外部环境扰动因素(如市场竞争行为等)的影响,其系统模型可以表示为[15,18-20]

上述(34)式所对应的二维确定性方程为

该方程存在一个稳定点(S −γ/c,0)与一个不稳定点(0,0).
根据第2 部分的引理和定理可得到(34)式对应的二维FPK 方程为

其本征值为
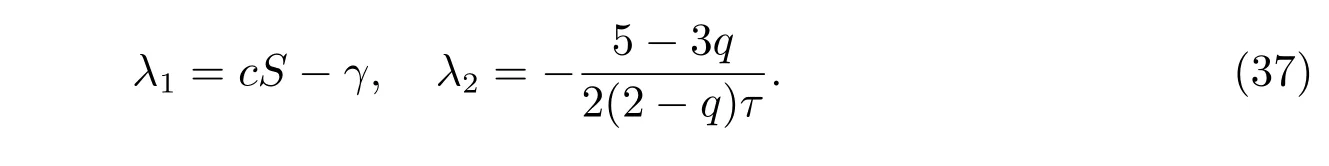
此时可进一步得到方程(34)式的非稳态解

其中N 为归一化常数.
通过(38)式,可将变量x 的n 阶矩表示为

特别地,变量x 的一阶矩为

接下来,我们根据方程(38)进行数值计算,这里给出不同非高斯噪声参数对p(x,t)影响的图像,具体如图1 至图5 所示.
图1 给出了非稳态解p(x,t)作为产量x 和时间t 的函数的三维图像.从图中可以明显看出,p(x,t)随着产量x 的增大单调递减最终趋于0,且当x 固定在较小值时,p(x,t)随着t 的增大而单调递减;当x 固定在较大值时,p(x,t)随着时间t 的增加先急剧增大出现峰值然后单调递减,之后随着t 的进一步增大,曲线变得越来越平缓,最终趋于稳定.当t 固定在较小值时,p(x,t)的峰值随着x 的增大在下降;当t 固定在较大值时,p(x,t)随着x 的增大在缓慢减小.上述变化正好验证了当新产品的产量x 较低时,社会对这种新产品的需求概率呈现出增加的趋势,这导致销售的数量会不断增大.但随着时间的流失,产量会继续增加,需求量会逐渐下降,直至达到饱和状态,生产也必然会停止.
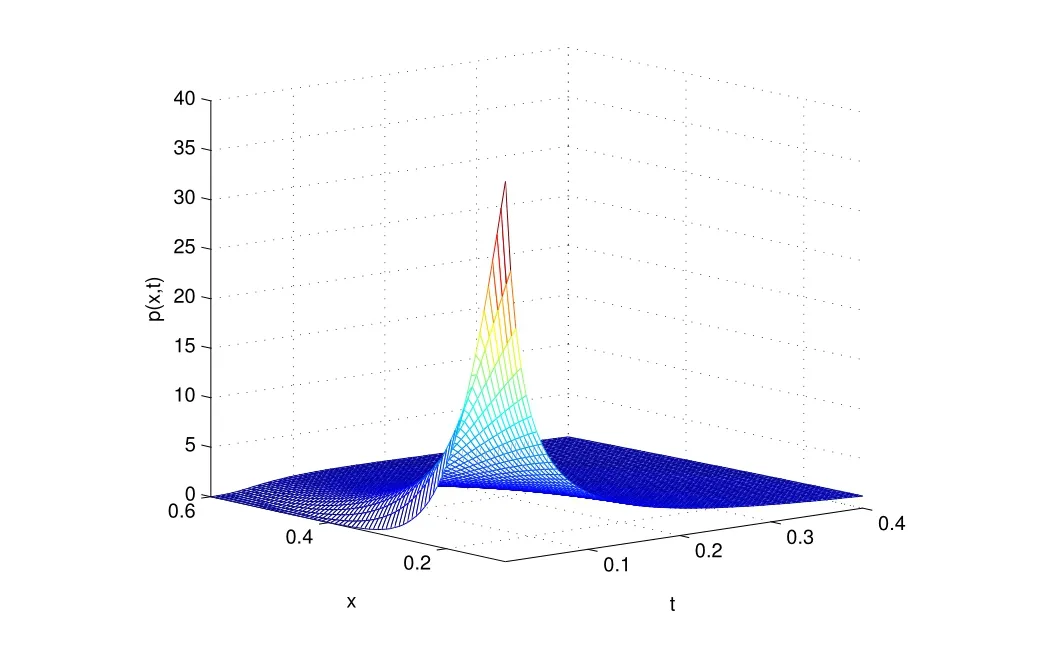
图1: 非稳态解p(x,t)作为产量x 和时间t 的函数(λ1 =1, Q=0.5, D =0.5, τ =0.5, q =1.05)
图2 和图3 分别给出了p(x,t)随x 和非高斯噪声强度D 及非高斯噪声关联时间τ 变化的图像,图4 和图5 分别给出了p(x,t)随x 和q 以及p(x,t)随t 和q 变化的图像.由图2 可知,当x 固定在较小值时,随着非高斯噪声强度D 的增大,p(x,t)单调递减,最终曲线趋于平缓;由图3 可见,随着非高斯噪声关联时间τ 的增大,p(x,t)单调递增;由图4 可见,当q 为定值时,p(x,t)随着x 的增大单调减小,最终趋于零;当x 为定值时,随着q 的增大,p(x,t)的值无明显变化.由图5 可见,当q 为定值时,在t 很小时,p(x,t)随t 的增大而急剧增大,出现峰值后,随t 的增大又单调递减,最终趋于零;当t 为定值时,随着q 的增大,p(x,t)的值无明显变化.图2 至图5 表明减小非高斯噪声强度D,并增大非高斯噪声关联时间τ 有助于商家盈利.

图2: 非稳态解p(x,t)作为产量x 和非高斯 噪声强度D 的函数(λ1 =1, Q=0.5, τ =0.5, t=0.1, q =1.05)
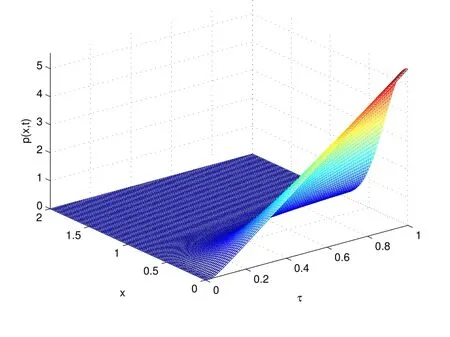
图3: 非稳态解p(x,t)作为产量x 和自相关时间τ 的函数(λ1 =1, Q=0.5,D =0.1, t=0.1, q =1.05)

图4: 非稳态解p(x,t)作为产量x 和非高 斯参数q 的函数(λ1 =1, Q=0.5, D =0.1, τ =0.5, t=0.1)
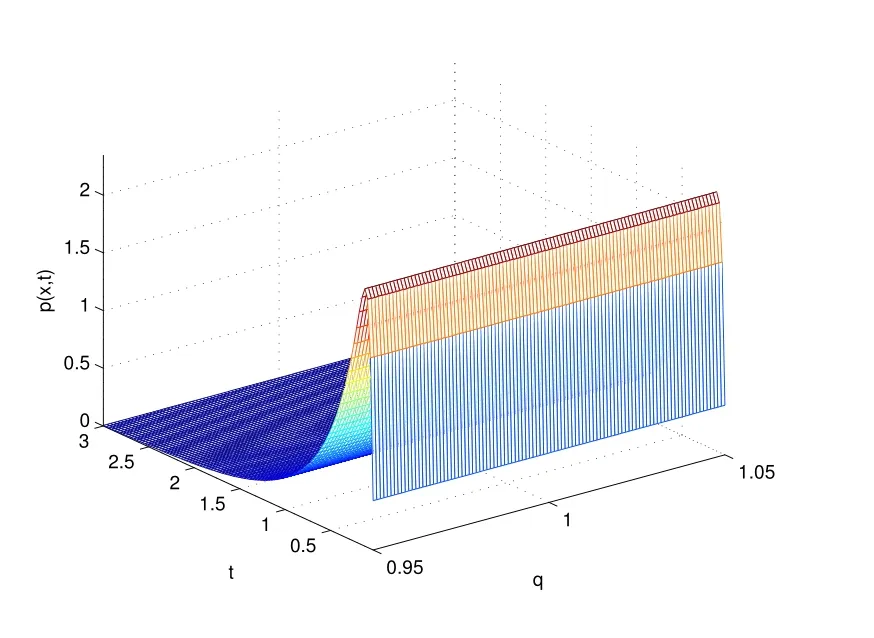
图5: 非稳态解p(x,t)作为时间t 和非高斯参数q 的函数(λ1 =1, Q=0.5,D =0.1, τ =0.5, x=0.5)
下面根据(38)式和(40)式,进一步给出均值〈x〉分别作为非高斯噪声关联时间τ 的函数和非高斯噪声强度D 的函数随着不同非高斯偏离参数q 变化的曲线,具体结果如图6 和图7 所示.
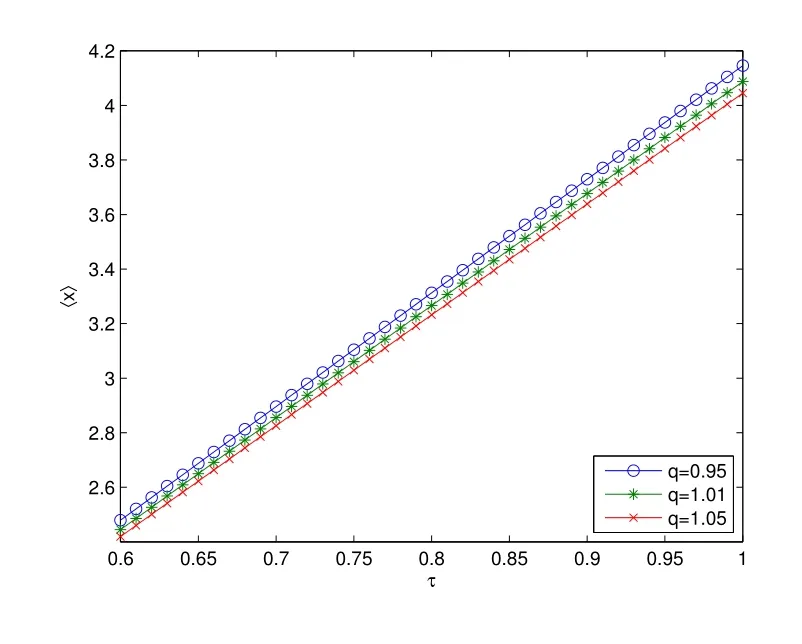
图6: 〈x〉作为自相关时间τ 的函数随不同 非高斯参数q 变化的曲线(λ1 =1, Q=0.5, D =0.5, t=0.01)
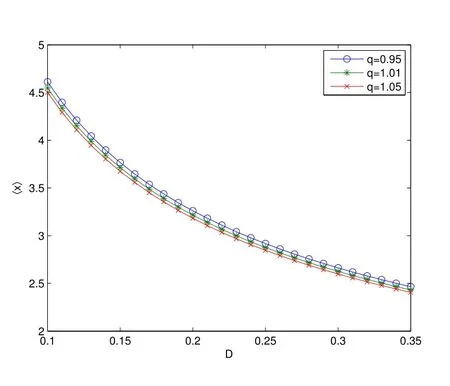
图7: 〈x〉作为非高斯噪声强度D 的函数随不同非高斯参数q 变化的曲线(λ1 =1,Q=0.5, τ =0.5, t=0.01)
从图6 中可以看出,当q 取定值时,〈x〉随着τ 的增大而单调递增,并且三条曲线的距离有变得越来越远的趋势.当τ 取定值时,〈x〉随着q 的增大而单调递减;从图7 中可以看出,当q 取定值时,〈x〉随D 的增大而单调递减,当D 取定值时,〈x〉随q 的增大也单调递减.综合以上分析可以得出:减小代表外部刺激的非高斯噪声强度D,增大非高斯噪声相关时间τ,同时减小非高斯噪声偏离参数q,将有助于商家盈利.
4 结论
本文主要研究了受非高斯噪声和高斯白噪声共同驱动的非线性动力学系统在不稳定区域的演化问题.首先应用格林函数的Ω 展开理论在初始时区域对非线性动力学系统进行线性化,然后利用本征值和本征矢理论得到了非稳态解p(x,t)的近似表达式,并以Logistic 系统模型为例分析了非高斯噪声的关联时间τ,噪声强度D 及非高斯噪声参数q 对p(x,t)以及一阶矩的影响.通过数值计算发现:当x 较大时,p(x,t)随着t 的增加出现单峰现象,且在一定范围内p(x,t)随着D 的增加单调递减,随着τ 的增加单调递增;此外,一阶矩随D 和q 的增加单调递减,随τ 的增加单调递增.上述研究结果表明在用Logistic 模型描述产品产量增长时,非稳态解p(x,t)可更好的反映产品产量在不稳定点附近的演化行为,对非稳态解的研究有助于商家制定更加合理的销售策略.

