海南省医疗卫生物资最优调配的数学建模(英)

1 Introduction

Because of the Hainan provincial special geographical position,geological structure and climate condition,it is imperative to build a relatively independent of disaster medical rescue system in Hainan island. It is even more important and eあective for Hainan island’s to rely on self-help rather than external assistance from other provinces and areas in China. There are eighteen major towns in Hainan province. Their names are Lingao (LG), Danzhou (DZ), Changjiang (CJ), Dongfang (DF), Ledong (LD),Sanya (SY), Baoting (BT), Lingshui (LS), Wanning (WN), Qionghai (QH), Dingan(DA), Wenchang (WC), Haikou (HK), Chengmai (CM), Tunchang (TC), Baisha (BS),Wuzhishan (WZS), Qiongzhong (QZ). Based on the rule of the maximum service distance reaching minimum, the center locations (towns) in these 18 major towns have been selected for the medical and health supplies reserve in [1]. There are three scenarios, the center locations include only one town (QZ), two towns (LD and TC), and three towns (CJ, DA and WZS). On this basis, we further research how to allocate the medical and health supplies from the given center locations (towns) to all other towns,such that the total ton kilometer numbers of the freight transport reach its minimum,in other words, how to make a transportation plan to minimize the total ton kilometer numbers of freight. This is what we are concerned about in this paper, so that the optimal allocation are obtained.

For convenience of modeling, we denote city’s name by a number code 1,2,··· ,18,respectively, these numbers are only the number codes for town names, see Table 1.Specifically, we will make some assumptions, the roads connected arbitrary two towns are passable, they are treated approximately as straight lines, and their lengths are known. The daily reserve amounts of the medical and health supplies in the center locations and the daily use amounts in the rest towns are supposed to know. We respectively consider three scenarios, one, two, three central points (towns), and determine the daily supply plan such that the total ton.km numbers of freight transport from the center points (towns) to all other towns reach the minimum.

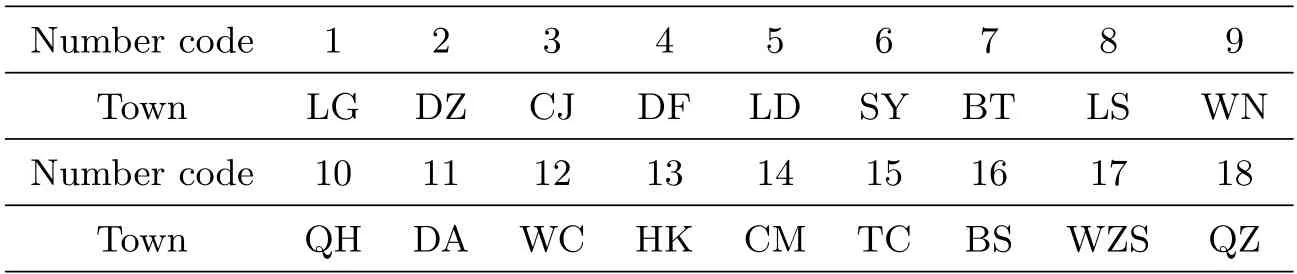
Table 1: Eighteen towns’ names and their corresponding number code

Lu[2]discussed the construction of the disaster medical rescue system of Hainan province. Zhang[3]considered the enhancement of the summarization of experience of medical rescue after Wenchuan earthquake. Qin et al[4]studied the geographic information system and the position of GIS for disaster medical rescue. Yan et al[5]studied the knowledge management of remedy of TCM based on the Wenchuan earthquake.Hu and Song[6]studied the actuality of domestic medical relief system for flood disaster. Cao[7]investigated the disaster relief medical practice innovation ideas and disease prevention strategies. Cheng et al[8]explored the engineering management of medical rescue in severe natural disaster. Chen et al[9]studied the role and model of three level hospitals in promoting community health service. Li et al[10]examined the payment risks of medical health care insurance fund and reform of medical health supply side.Wang[11]studied the large-scale hospital centered emergency medical supplies and reserve allocation system. Huang[12]examined the third sector and the supply of public goods in rural areas based on the medical and health supplies. Shen and Zhang[13]studied the supply side structural reform of China’s medical and health field. Dong et al[14]studied the current medical and health services supply in rural areas and its influence over patient-doctor relationship. Shi and Wang[15]explored the management mechanism of emergency supplies reserves in Chaoyang, Beijing, etc..

Common to all these studies is the no-use of mathematical models, rarely involves Hainan province,especially in the area of medical and health supplies. To the best of our knowledge,no studies has used the optimization modeling based on Floyd algorithm[16]for allocating the medical and health supplies reserve in Hainan province. If we treat the 18 major towns in Hainan as 18 points, the path between two towns is regarded as a line, and the distance refers to a weight, then a weighted and connected undirected graph is formed. The minimum spanning tree can be used to solve macroscopically the problem of minimum sum of length or minimum total cost. The Steiner tree problem in graphs refers to a tree of minimum weight that contains all vertices(but may include additional vertices), these two methods are mainly to find the optimal road. However,here we study how to make the optimal transport plan from the “center point” to all other “points”, such that the total ton kilometer numbers (transport amount multiply by transport distance) is minimized.

2 Mathematical modeling

With the distances (km) between any two towns of eighteen major towns[17]in Hainan province, by using Floyd algorithm[18]and Matlab software, the shortest distance matrix D = (dij), i,j = 1,2,··· ,18, and the shortest path index matrix R =(rij), i,j = 1,2,··· ,18, can be found between any two points (towns). According to the Floyd algorithm,the shortest distance matrix D =(dij)can be got via the weighted adjacency matrix W (see [1]).

R = (rij) is called the shortest path index matrix, rijdenotes the shortest path index between the i-th town and the j-th town,

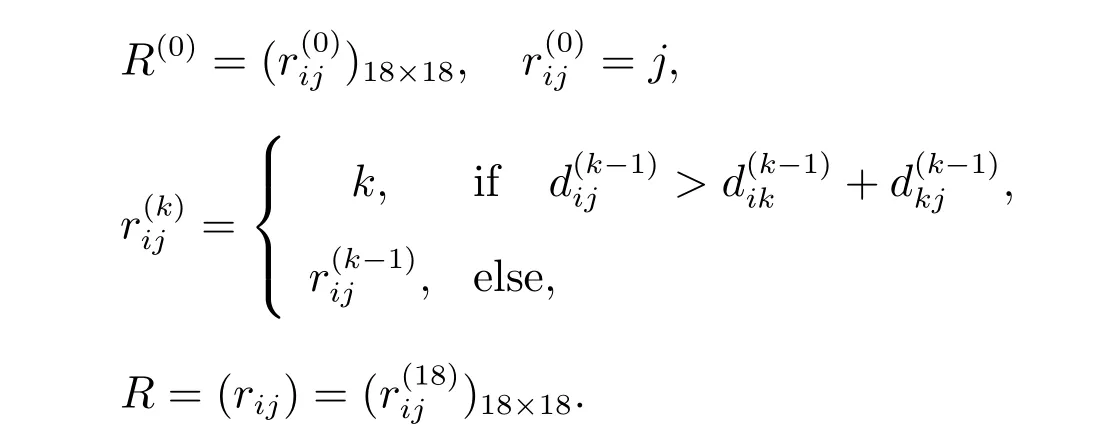
We tabulate the results about D and R in Table 2 and Table 3, respectively.

Table 2: Minimum distance (km) matrix D =(dij) between arbitrary two towns in Hainan province (first row and first column denote town’s number code (TNC))

For example, d13,5= 243(km) denotes the shortest distance from HK to LD, but its adjacent distances is 350(km) (see [1]), d13,5corresponds to r13,5, r13,5= 18 (see Table 3). We can insert one intermediate point 18 between 13 and 5, trace back from 18 in two sides, r13,18= 18, r18,5= 5 (see Table 3), it is obvious that the shortest path from HK to LD needs to go through an intermediate point QZ, the shortest path index is “13 −18 −5”, or, HK to QZ to LD. The shortest distance from SY to LG is d6,1=282(km), however its adjacent distance is 300(km) (see [1]), d6,1corresponds to r6,1, r6,1=17 (see Table 3), we can insert one intermediate point 17 between 6 and 1,trace back from 17 in two sides, r6,17= 17, r17,1= 16, r17,16= 16, r16,1= 2, r16,2=2, r2,1= 1 (see Table 3), so that, we can obtain the shortest path from SY to LG,it needs to go through three intermediate points WZS, BS and DZ, the shortest path index is “6 −17 −16 −2 −1”, or, the shortest path from SY to LG is SY to WZS to BS to DZ to LG. Similarly, we can obtain the shortest distance and the shortest path between arbitrary two towns in Hainan provincial eighteen towns from Table 2 and Table 3.

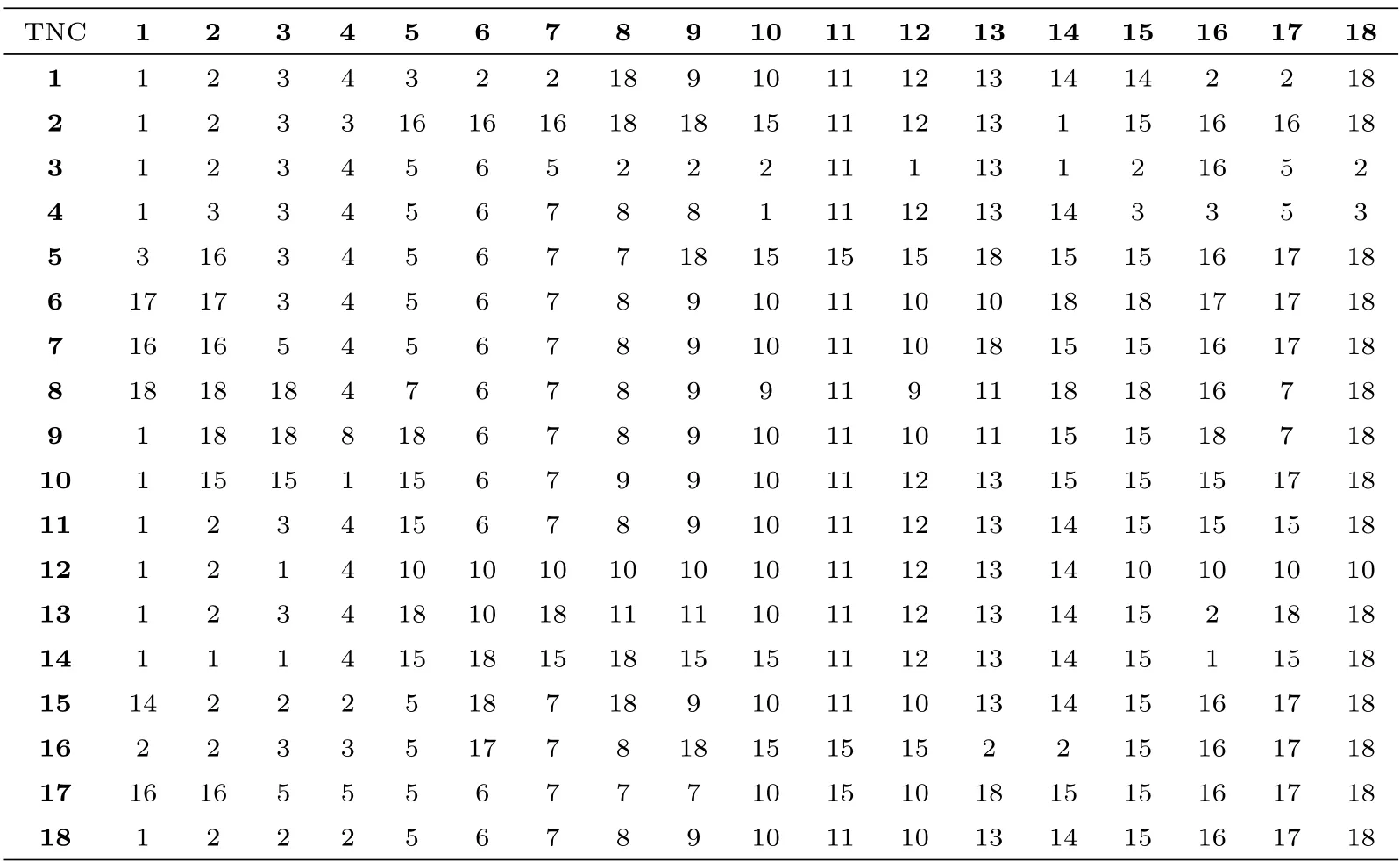
Table 3: The shortest path index matrix R=(rij) between arbitrary two towns in Hainan province (first row and first column denote town’s number code(TNC))

2.1 One center supply point (town) case—Qiongzhong (QZ)

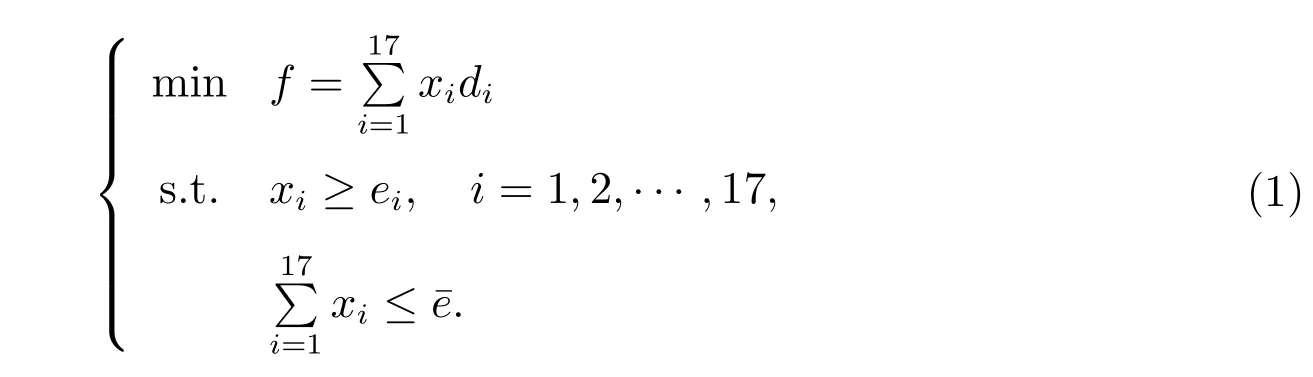
Because of xi≥0, it is obvious to see from (1) that when xi= ei, the objective function reaches the minimum value, or each town’s the daily supply amount is equal to its demand, or its use amount, but the transport route must be in the shortest path way. From the last row in Table 2 and Table 3, the shortest distances from QZ to LG,DZ,LD,SY,BT,LS,WN,QH,DA,HK,CM,TC,BS,WZS are 144,86.2,101,141,108,91.2,82.3,125,126,142,105,52.7,70.9 and 77.1(km),respectively,their corresponding shortest paths are to arrive directly, without an intermediate point. However, because r18,3= 2, r18,2= 2, r2,3= 3, the shortest path from QZ to CJ (the shortest distance is 162 km) needs to go through an intermediate point DZ, or, QZ to DZ to CJ. Since r18,12= 10, r18,10= 10, r10,12= 12, the shortest path from QZ to WC (the shortest distance is 184 km) needs to go through an intermediate point QH, or QZ to QH to WC. Since r18,4= 2, r18,2= 2, r2,4= 3, r3,4= 4, the shortest path from QZ to DF(the shortest distance is 220 km) needs to go through two intermediate points DZ and CJ, or QZ to DZ to CJ to DF.

We could consider establishing a central supply point outside of the 18 major towns in Hainan province from the mathematical point of view. Set a planar Cartesian coordinate system, take QZ as the origin of coordinates. Let (αi,βi), i=1,2,··· ,18, be the plane coordinate for the position of the i-th point(town),denoted by Ai(αi,βi), (X,Y)be the plane coordinate of the unknown center point, denoted by C(X,Y). On the other hand, there are the earth coordinates (longitude and latitude) of 18 towns, we might turn the earth coordinates (longitude and latitude) of 18 towns into their plane coordinates via some method. How to allocate the daily supplies of medical and health from the point C(X,Y) to all Ai(αi,βi), such that the total ton kilometer numbers of freight is minimized. Similarly, we can establish the mathematical model as where xi≥0 denotes the daily transport amount from C(X,Y) to Ai(αi,βi),(ton)is the daily reserve amount of medical and health supplies in C(X,Y), ei(ton) is the daily use amount in Ai(αi,βi),= max(dij). Model (2) is a nonlinear programming problem. If we can get the relevant parameters ei,,(αi,βi), the numerical solution xi, (X,Y) can be obtained from (2).

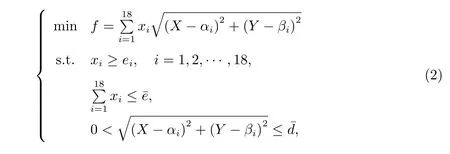
2.2 Two center supply points (towns) case—Ledong (LD) and Tunchang (TC)

How many medical materials are transported daily to other sixteen towns from LD and TC to make the total ton kilometer numbers minimized? Let x5,j, x15,j, j =1,2,··· ,18, j ̸= 5,15, x5,j≥0, x15,j≥0, respectively denote the daily transport amount(ton)from LD and TC to the j-th town,and5respectively denote the daily reserve amount (ton) of the medical materials in LD and TC,ek, k =1,2,··· ,18, k ̸=5,15, respectively denote the daily use amount (ton) of the rest sixteen towns, so that,we establish the mathematical model as follows

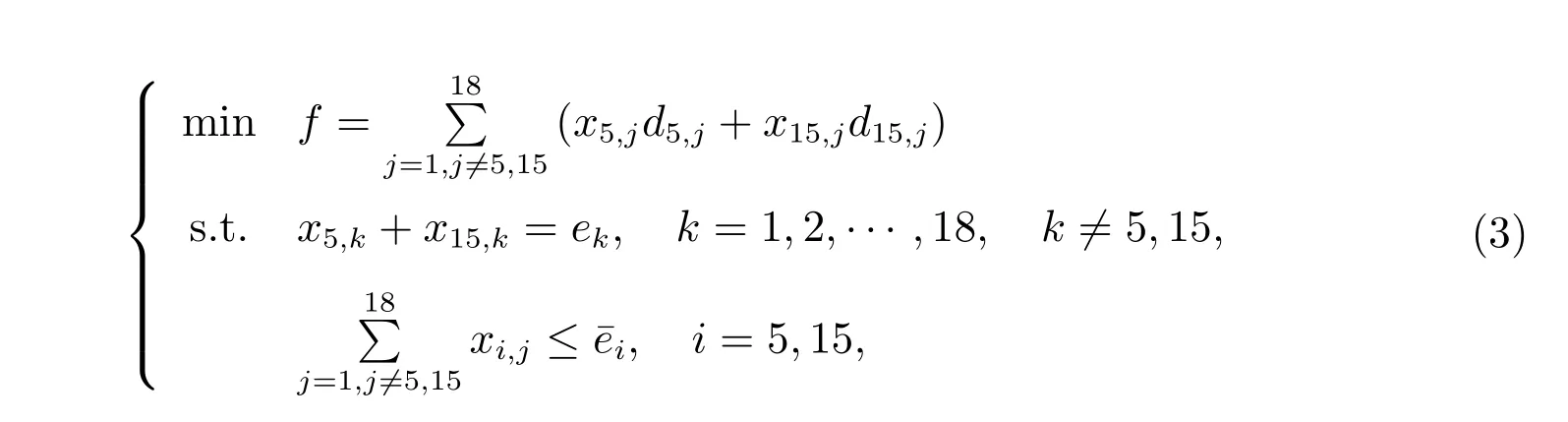
where d5,jand d15,jrespectively denote the shortest distance from LD and TC to the rest sixteen towns, the data are given in the fifth row and fifteenth row in Table 2,respectively. The shortest path indices are given in the fifth row and fifteenth row in Table 3,respectively. As long as we obtain the estimate value for the parameters ek,5and15by statistical methods, using the Lingo mathematical software[19], we can solve problem(3)to obtain x5,j, x15,j. So that, we can assign the daily supply plan from LD and TC to other sixteen towns.

Similar to the prior method described in section 2.1, we could consider setting two central points outside of the 18 major towns in Hainan province. Let the two unknown central points be Cj(Xj,Yj), j = 1,2. xij(≥0), i = 1,2,··· ,18, j = 1,2, denote the daily transport amount(ton)from Cj(Xj,Yj)to Ai(αi,βi).(ton)is the daily reserve amount of the medical and health supplies in Cj(Xj,Yj), eiis the daily use amount in Ai(αi,βi). How many medical materials are daily transported to all other towns from Cj(Xj,Yj)to make the total ton kilometer numbers minimized? We have the following mathematical model

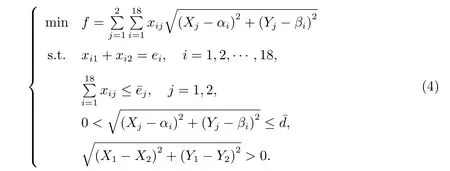
Model(4)is a nonlinear programming problem. If the relevant parameters ei,, (αi,βi)can be estimated, we can find the numerical solution xij,(Xj,Yj) from (4).

2.3 Three center supply points(towns)case—Changjiang(CJ),Dingan(DA) and Wuzhishan (WZS)

Let x3,j, x11,j, x17,j, j = 1,2,··· ,18, j ̸= 3,11,17, respectively denote the daily transport amount from CJ,DA and WZS to other fifteen towns,,1and7respectively denote the daily reserve amount of the medical materials in CJ, DA and WZS.ek, k =1,2,··· ,18, k ̸=3,11,17,respectively denotes the daily use amount of the rest fifteen towns. Similar to (3), we have the model as follows

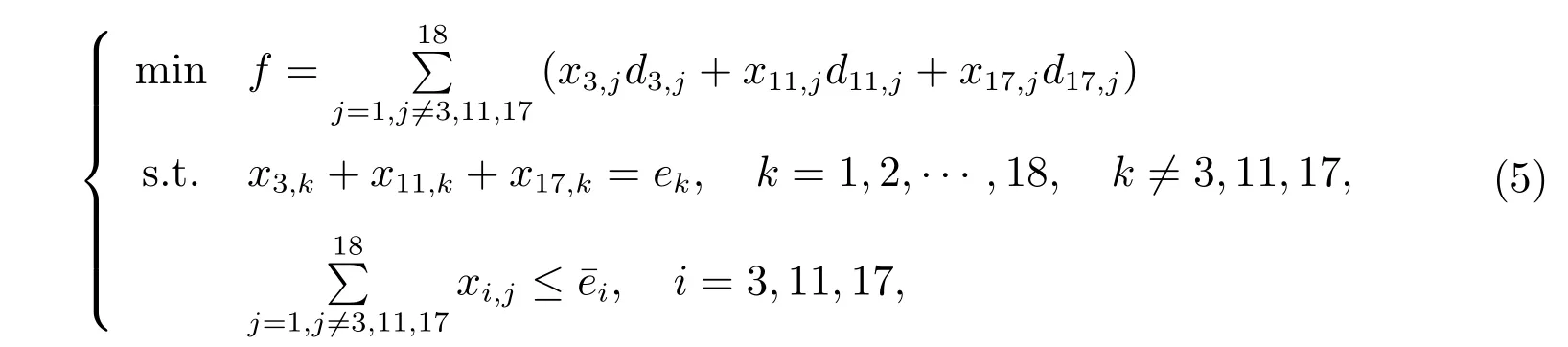
Similar to model (5), we could consider setting three central points outside of the 18 major towns in Hainan province. Let the three unknown central points be Cj(Xj,Yj), j =1,2,3, xij(≥0), i=1,2,··· ,18, j =1,2,3,denote the daily transport amount (ton) from Cj(Xj,Yj) to Ai(αi,βi).(ton) is the daily reserve amount of medical and health supplies in Cj(Xj,Yj),ei(ton)is the daily use amount in Ai(αi,βi).How many medical materials are daily transported to all towns from Cj(Xj,Yj),to make the total ton kilometer numbers minimized? We have the following model

Model (6) is a nonlinear programming problem. If we can obtain the relevant parameters for ei,and (αi,βi), the numerical solution xijand (Xj,Yj) can be got from(6).

2.4 Model parameter estimation and numerical results

In the models (1), (3), (5), the short distances are known, the reserve amount and the use amount of medical and health supplies need to be estimated by statistical methods (this is not our main work). If the estimate value can be got, we can solve numerically problem (1), (3), or (5), so the optimal supply plan can be made. Here,we do a simple and reasonable estimation for the reserve amount and the use amount,to illustrate the numerical solution of the models (1), (3) and (5). It doesn’t represent the reality, it’s just a simple reasonable simulation.

Let the per capita daily average use amount of medical and health supplies in Hainan province be ρ unit. It is known that the number of population in LG, DZ,CJ, DF, LD, SY, BT, LS, WN, QH, DA, WC, HK, CM, TC, BS, WZS and QZ. They are 38.9, 83.5, 22.0, 35.8, 44.6, 48.2, 14.0, 30.3, 52.2, 45.0, 28.0, 50.9, 83.0, 43.5, 25.3,16.5, 11.0 and 17.2 ten thousand (see[20]), respectively. These numbers are denoted by Zi, i = 1,2,··· ,18 (apart from the center supply points), then it is a reasonable assumption that the number ρZican be used as an estimate of the daily use amount of this town. For convenience, let ρ = 1 (one unit, for example, one ton). Because the center supply point (town), regardless of one, two, three supply points, needs to provide medical and health supplies, we cannot use simply the number of population of the town to estimate its daily reserve amount, a reasonable estimation is to use the total number of population of 18 towns, or, 689.9 ten thousand, to estimate the daily reserve amount of this supply point. By Lingo and Matlab mathematical softwares(see [21]), we can find the numerical results, which are given in Table 4.

Table 4: Daily optimal supply plan (tons) assigned for one, two and three supply points (ρ=1),one supply point (18); two supply points (5),(15); three supply points (3),(11),(17)

3 Model improvement

If we want to solve the models (1), (3), (5) optimally, it is necessary to find the daily reserve amount of medical and health supplies in the supply points and the daily use amount of the rest towns firstly. The accuracy of these data will directly aあect the numerical results of the models (1), (3), (5). It is a reasonable and simple estimation for the daily reserves amount and daily use amount in the previous section 2.4. If we want to obtain the accurate estimation value for the relevant parameters,we need to do further statistics works,and specific numbers need to be estimated further by statistical analysis. However, It will take a lot of time, energy and money. One cannot finish the work in a short time,it will be very diきcult. Lucky,this does not aあect the established optimization models (1)-(6). If we have the exact values for the relevant parameters,it is easy to get exact results of models (1)-(6) by utilizing the Lingo software and programming. Moreover,the time unit of daily reserve and daily transport amount can be weekly, monthly, etc., we can also get the weekly (monthly) optimal supply plan with the models (1), (3), (5). The number of supply points can also be expanded to four, five, and so on. The ideal situation is that each town has its own supply point,total 18 supply points. Since the area of Hainan Island is 35,000 square kilometers, 18 major towns,about 7 million population,it is not necessary for too many supply points.We have further promoted and considered other situations,obtained the corresponding models (2), (4), (6), no matter one, two or three supply points, the locations of the supply points don’t include in the eighteen major towns of Hainan province. Where are the new sites for building the supply points? How to make the optimal assignment plan under these new cases? We have models (2), (4), (6).

4 Conclusion

We have established the mathematical models for the optimal allocation of the medical and health supplies in the eighteen major towns in Hainan province. We respectively considered three scenarios, the site of one supply point located at QZ,two supply points at LD and TC, and three supply points at CJ, DA and WZS. We established optimization models (1), (3), (5), respectively, and obtained the optimal allocation plans using the statistical data of the eighteen major towns’ population and Lingo software. Moreover, we have expanded the model (1) to (2), (3) to (4), and (5)to (6), respectively. Models (2), (4), (6) have their theoretical significance.