起始扰动引起的跳角随靶距变化问题研究

邹玉华，张领科，王海峰

(1.南京理工大学 能源与动力工程学院， 南京 210094;2. 63850部队， 吉林 白城 137001)

射表是指导炮兵射击和编制火控软件所依据的基本文件，故射表的精度直接影响武器系统的射击精度。对于射表的精度，首先要射角满足的一定精度进而确保射程和偏流满足精度需求[1]。射角由仰角和跳角两部分组成，在仰角精度确定条件下，射角精度主要受跳角精度的影响，故开展跳角精度的研究成为国内外学者关心的重要课题[2-5]。

目前国内外对跳角的测量通常采用坐标靶，且往往只针对水平射击条件下的坐标靶弹着点坐标进行测试[6]。靶板法[7-8]是目前广泛采用的基于传统跳角定义下平射跳角测量方法。然而，试验结果表明，按该方法进行试验处理得到的跳角随靶距变化较大，某大口径火炮在56～226 m靶距范围内测得铅直跳角极差可达9.3分[9]。为解释这一现象，有文献[10]中提出了一般条件下的跳角定义，在该定义中包含了由起始攻角和起始攻角角速度引起的平均偏角对射角、射向的影响，将平均偏角归入跳角的一部分。目前关于跳角计算的理论建模研究较为少见。

为了深入认识线膛火炮测试跳角在起始扰动作用下随靶距变化的规律，本研究一方面基于弹丸仅受升力和静力矩作用下的简化情形，推导了由起始攻角角速度引起的平均偏角计算方法；另一方面，通过建立弹丸六自由度刚体外弹道模型，结合跳角计算公式，在假定起始跳角已知情况下对起始攻角、起始攻角角速度引起的跳角随靶距变化规律进行数值仿真，进而验证计算平均偏角方法的准确性，分析造成跳角随靶距变化的原因，对认识起始扰动对跳角随靶距变化规律的影响一定指导作用。

1 跳角

φ=θ0-γ

(1)

式中：φ为仰角；θ0为射角。

(2)

攻角方向的改变带来升力和马格努斯力方向的改变，导致速度方向不断改变，若只考虑对速度方向影响最大的升力项，描述速度方向变化的方程为

(3)

(4)

(5)

(6)

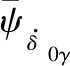
图1 一般条件下跳角定义示意图

(7)

按传统定义下跳角跳角测试结果应为与靶距无关的恒定值，而从表 1所示某大口径火炮在56～226 m靶距范围内铅直跳角实测结果[9]可以发现跳角测试值随靶距变化较大。在一般跳角定义下，弹道起始段呈渐收螺线规律，可以解释跳角随靶距变化的原因，本文将通过仿真模拟起始攻角与起始攻角角速度对跳角测试结果的影响。

表1 某大口径火炮铅直跳角γ(′)实测值

图2 平射跳角试验示意图

2 仿真模型

弹丸出炮口后的运动规律通过6自由度刚体弹道方程描述，建立在速度坐标系下的弹丸质心运动的运动学方程和弹轴坐标系下的弹丸绕质心运动的运动学方程如下[11]，

(8)

式中：t为时间(s)；v为弹丸速度(m/s)；θa为速度高低角(rad)；ψ2为速度方向角(rad)；ωξ、ωη、ωζ为弹丸绕质心转动的总角速度ω在弹轴坐标系的三个分量(rad/s)；φa为弹轴高低角(rad)；φ2为弹轴方向角(rad)；γd为弹体自转角(rad)；x、y、z为基准坐标系下质心坐标(m)；FX2、FY2、FZ2为弹丸所受合力在速度坐标系的3个分量(N)；Mξ、Mη、Mζ为弹丸所受合力矩在弹轴坐标系的3个分量(kg·m2)。FX2、FY2、FZ2与Mξ、Mη、Mζ的表达式参考文献[11]。弹丸角约束方程为

(9)

式中：δ1为高低攻角(rad)；δ2为方向攻角(rad)；β为第一弹轴坐标系与第二弹轴坐标系间的转角(rad)。

为利用上述弹道方程模拟平射跳角试验，提出如下基本假设条件：

1) 仰线与基准坐标系OXNYNZN中OXN轴重合，质心坐标x即为靶距；

2) 发射前后炮口中心位置不变；

3) 忽略后效期膛口流场对弹丸的作用；

4) 气象为标准气象条件、无风。

(10)

(11)

通过给定不同的初始条件模拟起始攻角和起始攻角角速度变化，利用龙格库塔法解算上述模型得到弹丸质心坐标与时间，代入跳角计算公式即可模拟在不同靶距下测试跳角的结果。

3 跳角变化规律的数值仿真

针对某155 mm榴弹，基于式(7)～式(11)所建立的试验跳角计算模型和弹丸刚体弹道模型，编制仿真程序，计算由起始攻角和起始攻角角速度引起的跳角变化规律。弹丸的结构参数如表2所示，弹丸部分气动数据如图 3所示，通过拉格朗日插值可得不同马赫数下各气动系数，射击地理条件为纬度45°，阵地海拔高度0 m，射击方向与正北方的夹角为5°。

表2 弹丸结构参数

图3 零升阻力系数-马赫数与升力系数-马赫数散点图

3.1 起始攻角引起的跳角随靶距变化

从图 4与图 5可以看出：在50～300 m靶距范围内，起始攻角δ0为最大取值δ10=9′，δ20=9′时，铅直跳角极差|Δγ|最大，约为0.226′；起始攻角δ0为最小取值δ10=1′，δ20=1′时，方向跳角极差|Δω|最大，约为0.646 5′。对比表1所示56～226 m靶距范围内某大口径火炮铅直跳角实测结果可以发现，相较于铅直跳角极差|Δγ|可达9.3′的实测结果，可以忽略较小的起始攻角δ0引起的跳角随靶距的变化。

表3 仿真初始条件

图4 δ0引起的γ-x曲线

图5 δ0引起的ω-x曲线

3.2 起始攻角角速度引起的跳角随靶距变化

在前一小节中验证了较小的起始攻角不是造成跳角随靶距变化的原因，本节将探讨起始攻角角速度对跳角随靶距变化的影响。仿真中将起始攻角δ0大小设置为0，即弹轴方位与初速方位重合。初始条件设置如下：弹丸角速度分量ωη、ωζ均为5 rad/s，弹轴高低角φa与弹轴方向角φ2均为-0.001 454 41 rad，其他参量与表 3相同。

计算两种不同工况下跳角随靶距变化，工况1：考虑弹丸仅受升力和静力矩作用下的简化情形，将仿真模型中合力和合力矩分量分别用升力与静力矩分量代替，由于不计重力，式中铅直跳角应为

(12)

式中：γsimplify为此简化情形下铅直跳角值；工况2：考虑弹丸在全力组与全力矩作用下的一般情形。计算得两种不同工况下铅直跳角与方向跳角随靶距变化曲线分别如图6和图7所示；计算得工况1下质心运动轨迹如图8所示。

图引起的γ-x曲线

图引起的ω-x曲线

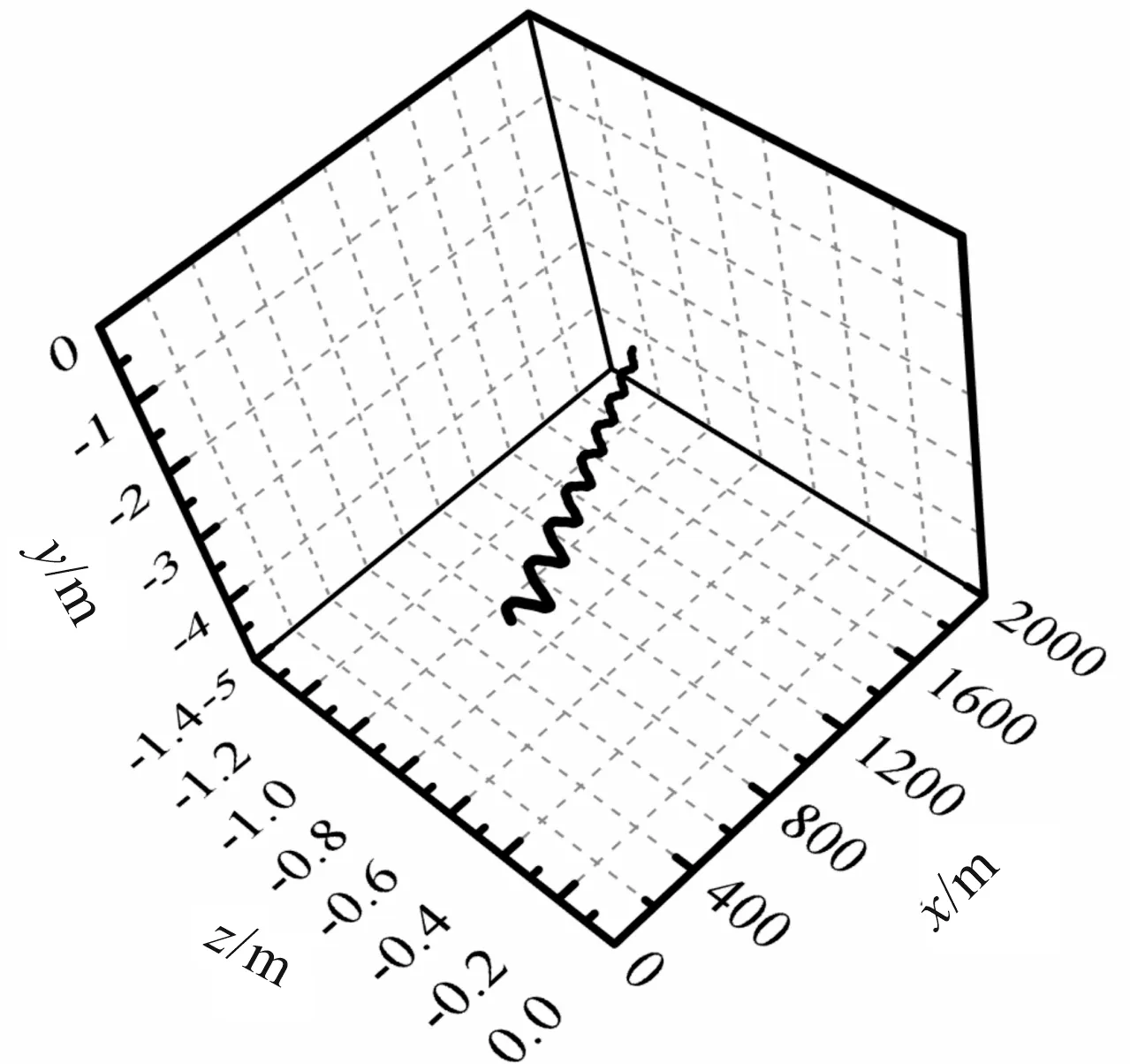
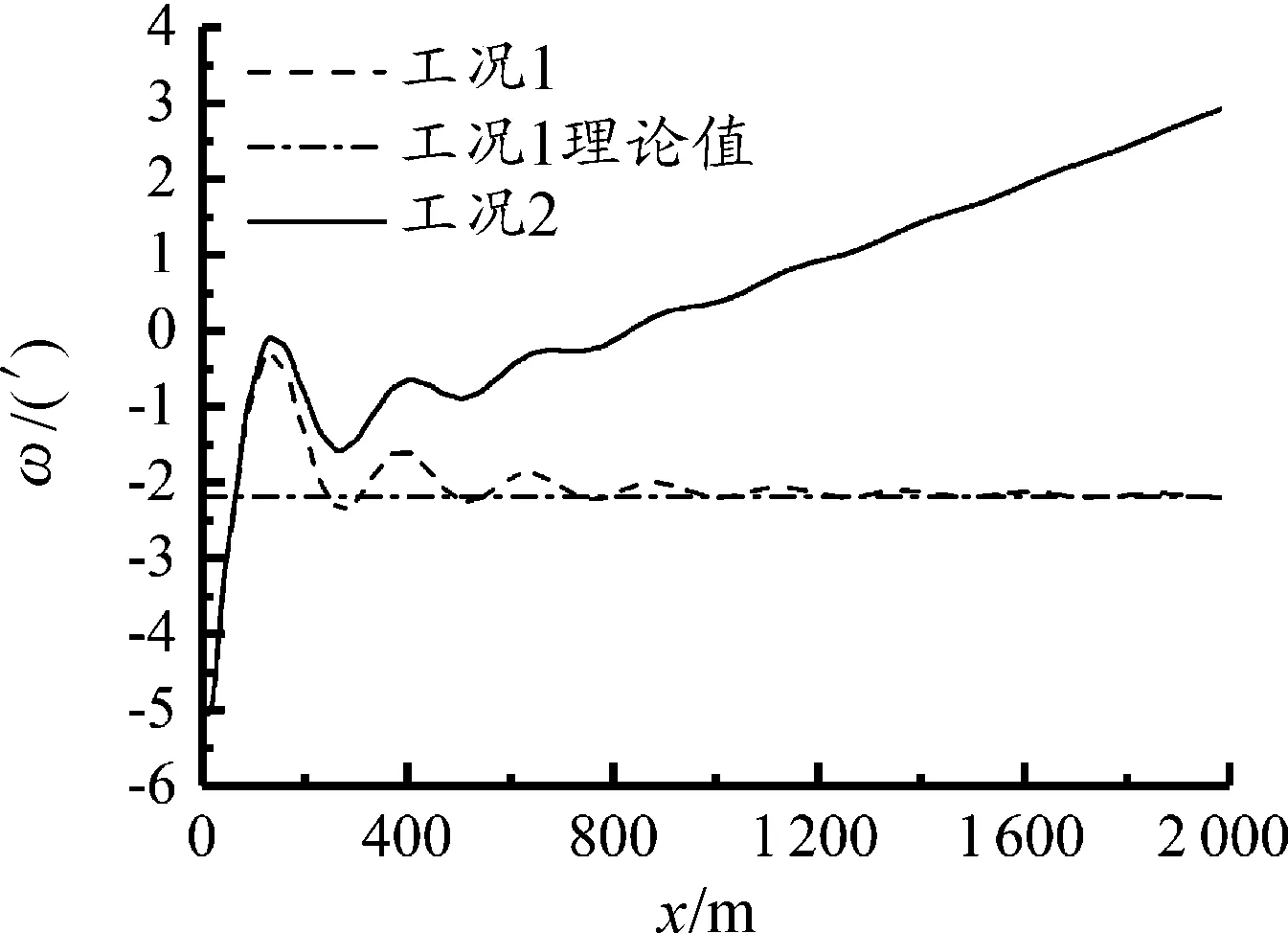
图8 简化情形下引起的质心运动轨迹

3.3 起始攻角角速度散布时跳角变化规律

图散布时靶距100 m落点散布图

图9中落点坐标(y，z)均值为(-0.201 83 m，-0.015 13 m)，从图10、图11可以发现：靶距100 m时铅直跳角和方向跳角结果在攻角角速度服从正态分布时也服从正态分布。

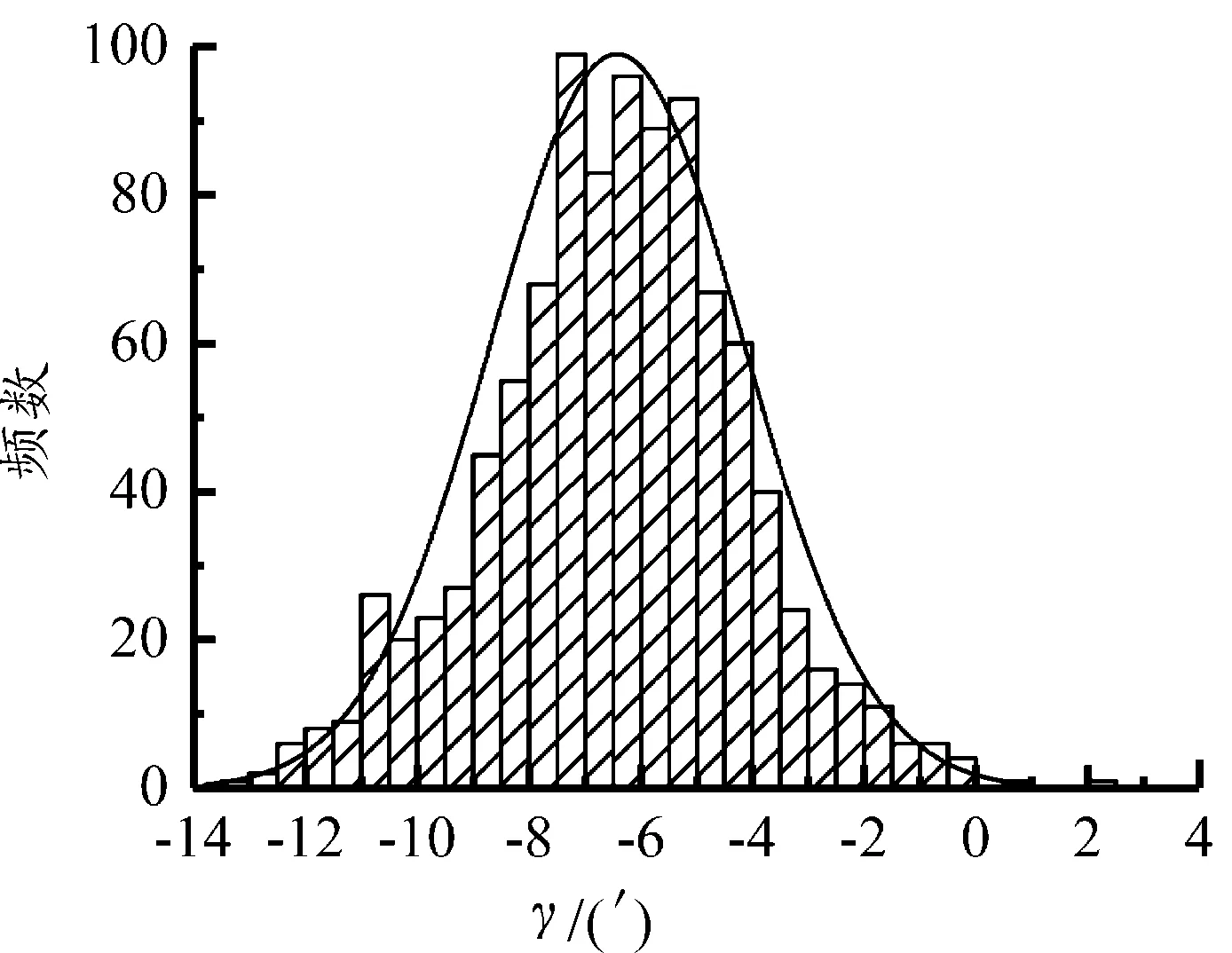
图10 靶距100 m处γ频数分布直方图

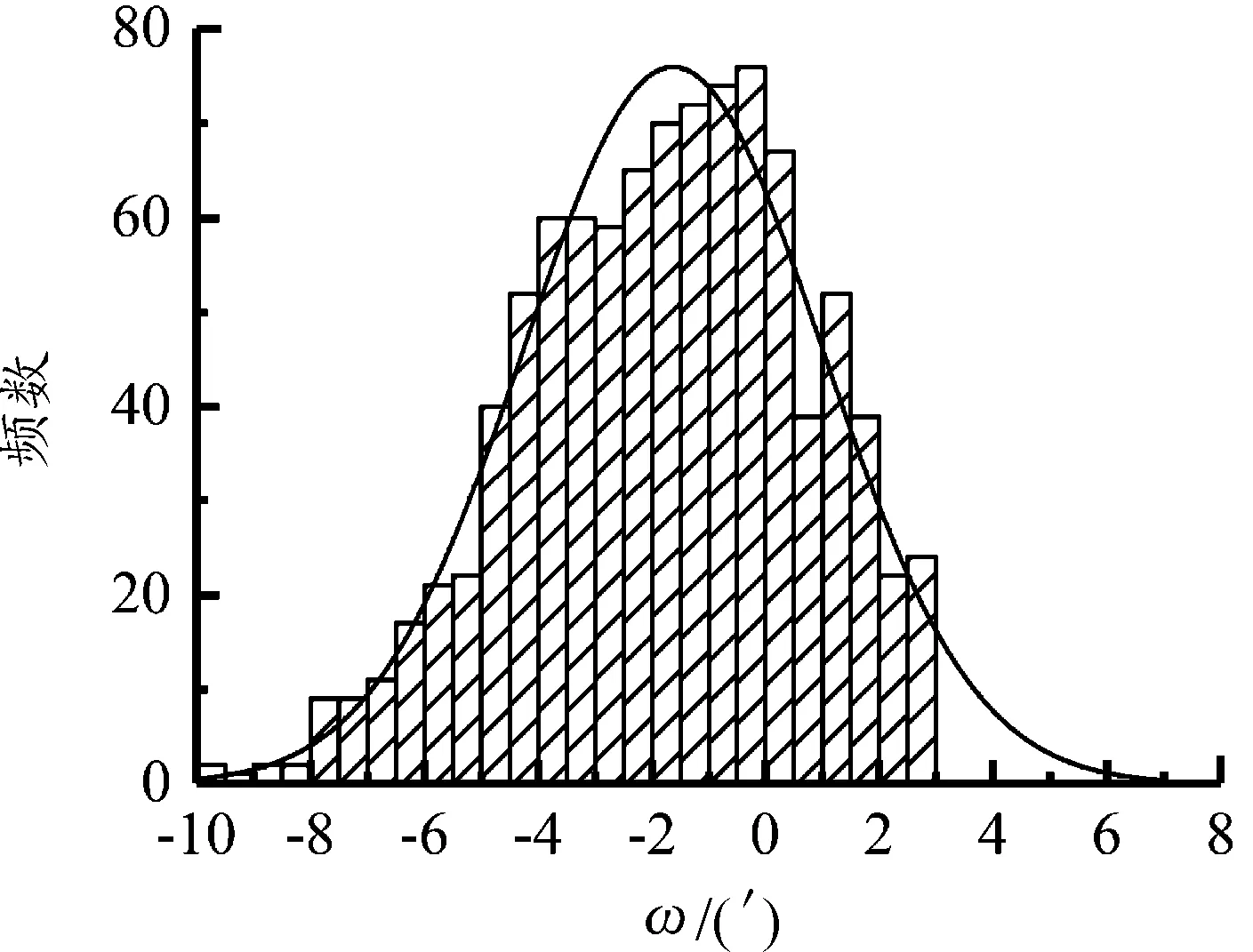
图11 靶距100 m处ω频数分布直方图

为研究跳角散布与起始攻角角速度散布的关系，计算了不同靶距、不同起始攻角角速度均方差条件下铅直跳角和方向跳角均方差如图12与图13所示。

图曲线

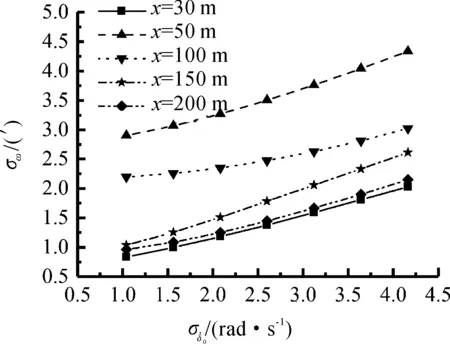
图曲线

从图12与图13中可以发现：① 同一靶距下铅直跳角和方向跳角均方差随着起始攻角角速度均方差增加而增加，近似服从线性规律；② 在相同的起始攻角角速度均方差条件下，不同靶距处的铅直跳角和方向跳角均方差不等。

4 结论

1) 一般线膛火炮在跳角测试时可以忽略由较小的起始攻角引起的跳角随靶距的变化，起始攻角角速度是造成跳角测试值随靶距变化的主要原因之一；

2) 靶距较小时起始攻角角速度引起的跳角随靶距变化结果在全力组和全力矩作用结果，与只考虑升力和静力矩时的简化情形结果一致，靶距较大时在全力组和全力矩作用跳角结果呈逐渐增大的趋势，因此试验时应选取合理的靶距；

3) 起始攻角角速度服从正态分布时某一靶距下的跳角结果也服从正态分布，且跳角的散布大小与起始攻角角速度的散布大小近似具有线性关系。