正弦交叉波纹填料三维换热特性的数值模拟

辛军哲，曹旭楠，李应新

1.广州大学，广东 广州 510006 2.华润置地商业管理服务（深圳）有限公司，广东 深圳 518000 3.东莞森博科瑞莱空气制冷有限公司, 广东 东莞 523000

交叉波纹填料的流体通道是由两片波纹板按一定角度相互交叉叠放所形成的相互连通的空间。由于该通道的特殊结构形式，流体流经时的速度大小和方向都会发生周期性的变化，并产生大小不同的漩涡，可以大大强化其内部的热质交换过程，被越来越广泛地用作多种用途的热质交换设备。为了使这种结构简单、加工方便的通道及其填料的传热传质效率更高，流动阻力更小，许多研究者[1-9]利用实验的方法得到了不同条件下的阻力特性和降温特性，有的采用可视化技术得到了通道内流动和换热局部形态图像。

越来越多的研究者采用计算机模拟技术，对其流动和热质交换过程进行模拟计算研究。杜鹃等[10]和Wu等[11]将交叉波纹通道填料内流场简化为一个二维气体流场，采用零方程紊流模型得到了该填料水平面上温度场和相对湿度场分布，分析了不同因素对交叉波纹通道填料蒸发冷却效率及出口空气状态的影响。Beshkani等[12]近似假设两波纹板之间通道的流动在两波纹板几何分界面两边对称分布，不考虑两波纹板通道间流动的相互影响，将蒸发冷却用交叉波纹通道内复杂的流动看成由一个个沿着边界形状不变的对称波纹槽内流动组成，对半正弦单元的流动进行研究。其假设气体做层流流动且忽略流动方向上扩散的影响，计算得到流场的速度分布和温度分布。Poulter等[13]将两个波纹板之间的交叉波纹通道近似地按照两个平行平板间的流动进行处理，通过数值求解的办法计算了一小型单壁垫片式换热器内的流动和温度分布。Zhao等[14]对两波纹片在流动方向和迎风方向含有多个通道区域的流场和温度场进行了数值模拟，但其计算结果仅给出了两波纹片间几何分界面处温度场、压力场和速度场的分布，对流动的细节，尤其是壁面附近的流动和换热没有给出较为详尽的描述。

要详细地了解交叉波纹通道内流动和换热规律，分析各结构参数对流动和换热性能的影响，就必须在速度梯度大的位置布置密集的网格。Doo等[15-16]对交叉波纹通道热交换器的具有代表性的单元，利用低雷诺数模型分别计算了不同几何结构参数下的流动特性。Ciofalo等[17]对一个标准交叉波纹通道单元，分别采用层流模型、标准k-ε模型、低雷诺数模型、直接模拟方法以及大涡模型计算了其局部换热特性和阻力特性。Mehrabian等[18]对此交叉波纹通道热交换器的一个标准单元，按照层流假设，进行了其速度场、压力场和温度场的微观计算。辛军哲等[19]对由两片相互交叉的正弦波纹板所形成的三维通道，按照实际流动边界条件运用低雷诺数k-ε紊流模型进行全流场流动的计算，得到了该计算域流场速度场和压力场在宏观和局部微观区域的分布特点。

综上所述，现有对正弦交叉波纹通道三维换热特性的研究大多局限在对其标准单元格或其简化通道结构进行。但像蒸发冷却系统所用的这类正弦交叉波纹填料通道，其沿流动方向的厚度一般都很小，大多为60～150 mm，其流动主要处于发展流阶段，未进入充分发展状态，按照充分发展状态的标准单元格所计算的结果与实际有较大偏差。本工作将在辛军哲等[19]计算域和计算模型的基础上，进行三维换热特性的数值模拟，期望得到总的蒸发冷却效率随进口风速的变化规律，更重要的是得到波纹通道不同单元格内的局部传热特性的影响因素及其变化规律，以便用于正弦交叉波纹填料的设计改进。

1 物理模型及假设

研究对象如图1所示。两层波纹高度为7 mm、波距为20.5 mm的正弦波形波纹板，以波纹通道间成90°夹角粘接在一起，形成一个完整的正弦交叉波纹填料通道。气流沿X方向进入该两片波纹板间，两片波纹板通道与进口气流方向成相互交错的45°夹角。Z方向计算域边界为固体边壁，将气流局限于在计算域内流动。计算域X方向尺寸为75 mm，Z方向为145 mm，Y方向最大为14 mm。为了保证两片波纹板内流动的对称性，两片波纹板的通道布置完全相同。

图1 计算区域结构示意Fig.1 The structure diagram of computational area

图2为计算域X-Z平面视图，前后两片波纹板在Y方向堆叠而成。计算域内的细实线代表其中一波纹板的波峰线，相邻两细实线之间即为其计算通道，各通道分别用不同的大写字母表示。虚线为与其对应的另一波纹板的波谷线，相邻两虚线之间即为其计算通道。作为示例，在图中用箭头示出了细实线A通道内的气流主流动方向。当该通道内的气流碰到边壁后，即流入另一波纹板虚实线内的通道。而由于结构的对称性，相同的情况会发生在图中上面对应的位置，只是交换了前后波纹板内的对应通道。所以，为了方便分析主气流通道内参数的变化情况，将两段同字母代号的细实线波纹通道看成是一个完整的通道来一起分析。各通道字母代号的下标数字（i）代表通道过流断面位置，其中1代表进口断面，6代表出口断面，2～5分别代表与另一波纹板波谷的交界位置。同一通道的相邻两个过流断面之间的区域称之为单元格，并用前后两个断面的数字表示。计算域物理模型处理方法与文献[19]的相同。

图2 波纹片波纹通道图示Fig.2 Corrugated groove channel diagram

交叉波纹通道壁面被水湿润，空气流经该通道时，水直接蒸发并使空气冷却降温。该过程不但涉及气相流动，同时还存在着液相流动，本工作做了如下简化假设：

（1）整个流动和换热过程在稳定状态下进行；

（2）忽略计算工况条件下的流体物性参数变化，并忽略质量力；

（3）波纹通道表面正好被水完全润湿，且形成一层均匀的水膜，忽略水膜厚度和其流速；

（4）直接和水膜接触的薄层空气是饱和的，其蒸汽分压力等于水膜温度下的饱和压力，该饱和空气层厚度忽略不计，并符合无滑移边界条件；

（5）水膜温度恒定且等于入口空气的湿球温度，忽略水蒸气的显热；

（6）计算域中的空气和水均与外界处于一个绝热的环境。

2 控制方程及其求解方法

2.1 控制方程及紊流模型

空气在该蒸发冷却过程中的控制方程包括连续性方程、运动方程和能量方程：

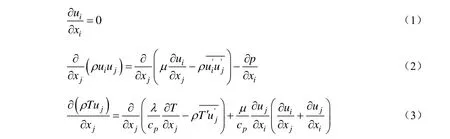
式中：μt为紊动黏度，采用Jones-Launder的低雷诺数k-ε模型进行模拟[19]。

2.2 边界条件

进口边界条件：

空气流速：ux=u0，uy=0，uz=0

空气温度：T=T0，TW=TW0

式中各参数取值见文献[19]。出口边界条件按照局部单向化边界条件处理。

壁面边界条件：

空气流速：ux=0，uy=0，uz=0

式中：Wj为水分蒸发离开气液介面的质量流率[20]。

2.3 求解方法

使用ANSYS Meshing对计算域进行网格划分，采用非结构化四面体网格。为有效求解近壁处较大的速度和温度梯度，在近壁面附近布置相对较密的膨胀层，最终网格总数为16 829 606。将划分好的网格导入到ANSYS Fluent15.0中，并对区域材料以及边界类型进行设定[19]。

选用低雷诺数k-ε紊流模型，采用速度和压力耦合的半隐式SIMPLE算法，压力项采用线性插值。为了加快迭代收敛的速度，改变动量方程的松弛因子为0.8，其他保持默认值。除了能量方程默认的残差值为10-6以外，其余各方程参数的残差都默认为10-3。

3 模拟结果及分析

3.1 蒸发冷却效率随风速的变化

该填料在进口沿X方向上不同风速下的蒸发冷却效率模拟结果如图3所示。由图3可见，产品资料数据[21]、实验数据[4]和模拟结果三组数据均显示出蒸发冷却效率随风速的增加而减小的基本趋势，并且各组数据之间十分接近，尤其是模拟结果与产品资料数据[21]的一致性更好。

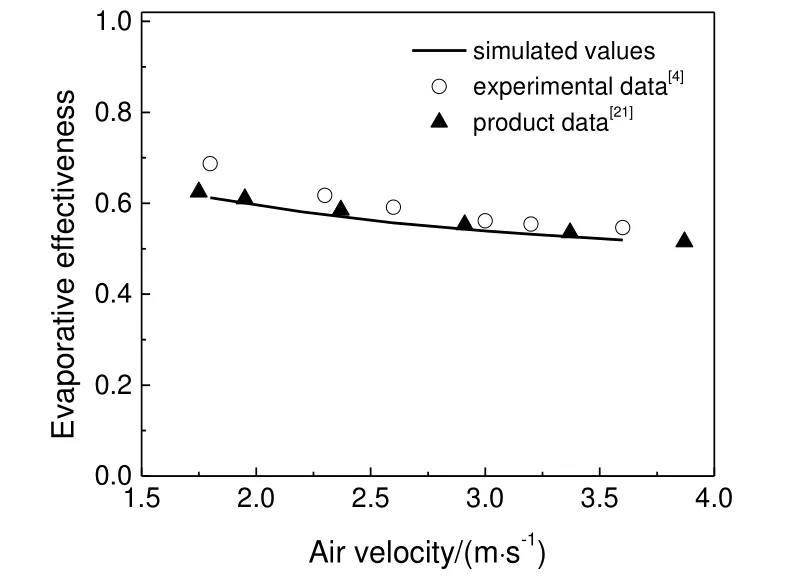
图3 蒸发冷却效率随风速的变化Fig.3 Evaporative effectiveness with air velocity

3.2 各波纹通道温度的变化

在这种由相互成一定角度排列的交叉通道内，由于两片波纹板间通道相互连通，并受到上下边壁的影响，各通道内的流动十分复杂，且互不相同，导致各通道内的流量、压力以及温度也互不相同。图4绘出了在进口气流速度为1.8 m/s、干球温度为35 ℃、湿球温度为21 ℃时各波纹通道不同截面上质量平均温度曲线，其各通道代号及其下标i代表的截面位置如图2所示。由图4可看出，各波纹通道内的温度均为单值下降，并且开始温度下降较快，后面温度下降较为平缓，符合理论预期。而从各个通道内温度变化曲线的相互比较来看，各通道温度变化相近，只是A通道的温度明显较其它通道的温度低。在最为明显的第5截面上，A通道此时的温度比其上一个截面4的低1.58 ℃，而其他通道此时的温降为1.20～1.28 ℃，大约是这些通道平均温降的1.27倍。但在第5和第6截面之间，其他通道的温降大多为0.99～1.14 ℃，而此时A通道的温降却只有0.79 ℃，明显小于其他通道。最终在出口断面上，最低温度的A通道与最高温度的D通道的温度差约为各通道平均温降的7.1%。

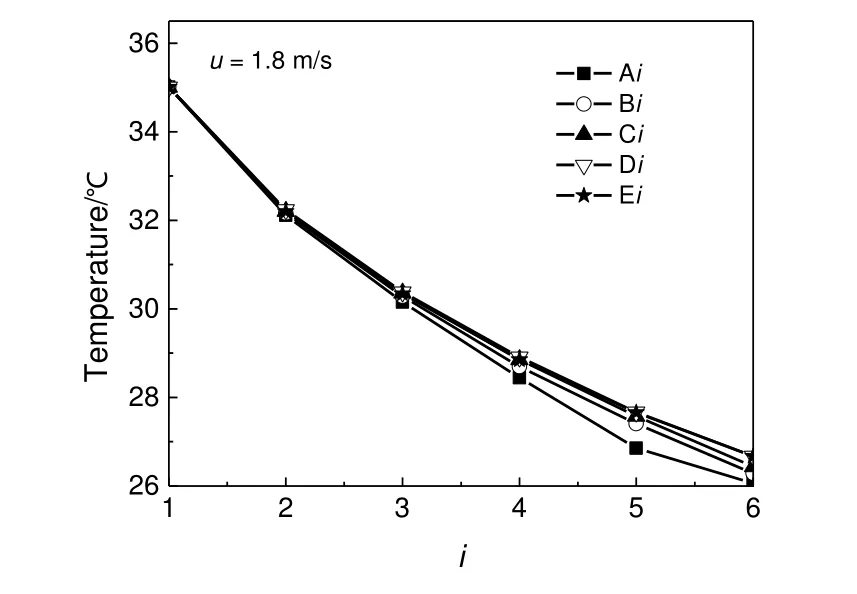
图4 各通道不同截面上的温度Fig.4 Temperature at different sections of each corrugation

3.3 各波纹通道热流密度的变化

上述各波纹通道温度沿通道流动方向的变化规律，除了与各通道的流量变化和各通道流体之间的对流换热有关外，很大程度上还与各通道的热流密度有直接的关系。为了研究各通道热流密度对其温度变化的影响，图5为在图4的进口条件下各通道内单元格平均热流密度沿波纹通道主流动方向的变化曲线，其各通道代号及其下标i相邻两数字所代表的单元格位置如图2所示。由图5可以看出，热流密度受主流动区域温度逐渐下降的影响，其数值的变化趋势与温度变化趋势相同，均为单值减小，开始减小较快，后面减小较慢。而从各个通道内热流密度变化曲线的相互比较来看，相同位置单元格的各通道热流密度相近，只是A通道在单元格4-5内的热流密度明显高于其他通道在这一单元格上的值。在该单元格位置上，A通道的热流密度比热流密度最小的B通道的值高出21%，而其他通道与B通道的热流密度差最大也就是6.2%。由于单元格4-5在第4和第5断面之间，A通道在此单元格上热流密度相对于其他通道的显著增加，将会直接增大空气与水的换热量，从而使A通道如前所述，在第5断面上的温度明显低于其他通道。从图中也可以看出，A通道在单元格5-6内，其热流密度为394.3 W/m2。而在此单元格位置内，其他通道的热流密度均在402 W/m2以上。A通道此时的值显然小，但并未小很多。而由图4可知，A通道在此单元格内的温降却比其他通道的要小很多。其主要的原因是，A通道在单元格5-6内由另一波纹片对应的C通道混入大量的高温空气，最终导致其在没有充分与水进行换热降温的情况下而使温降大大减小[19]。有趣的是，A通道在单元格4-5内同样由另一波纹片对应的B通道混入大量的高温空气，但由于其有足够大的热流密度与水进行换热降温，最终仍能产生很大的温降。

图5 各波纹通道不同单元格热流密度Fig.5 Heat flux of different unit of each corrugation

3.4 各波纹通道切应力的变化

影响热流密度大小的因素很多，但对这种交叉波纹通道来说，各通道之间的主要区别是气流受边壁的影响所产生的扰动不同。而切应力作为反映近壁附近流动情况的一个重要指标，其大小会与热流密度的大小紧密相关。图6为在图4的进口条件下各通道内单元格平均切应力沿波纹通道主流动方向的变化曲线。由图6可以看出，切应力的变化趋势与热流密度的变化趋势相似，但要分散得多，相同位置单元格的各通道的切应力相差较大。由最为典型的单元格4-5上各通道的切应力比较来看，A通道的切应力最大，B通道的切应力最小，相应其热流密度也是A通道的为最大，B通道的为最小，规律相同。但从具体的数值来看，A通道在单元格4-5内的切应力比对应单元格切应力最小的B通道的值高出37%，甚至比其上一个单元格3-4的切应力还高出21%，而B通道单元格4-5的切应力比单元格3-4的实际上是小14%。而在图5中，A通道的热流密度比B通道的值仅高出21%，其比上一个单元格3-4的值小4.8%，尽管其减小的值比B通道减小的21.1%要少很多。之所以出现这一现象，主要就是热流密度的大小不单受切应力的影响，还会受到主流气流温度的影响。主流气流温度越高，与填料表面的水温温差越大，其热流密度相应也会增大，反之则会变小。在上述单元格4-5内，尽管A通道的切应力很大，甚至比单元格3-4内的切应力还大，但由于其温度最低，所以最终它的热流密度尽管在同单元格内是最大的，但比上一个单元格还是要小一些，尽管小的很少。类似的情况，在其他通道的各单元格上同样可以看到。如在单元格5-6位置上，尽管A通道的切应力较高，但由于它的温度相比其他通道明显要低很多，最后导致其热流密度和B通道的差不多，处于最低水平。当各单元格的温度相近的时候，如上述单元格1-2，2-3和3-4位置处的各通道，此时其热流密度主要受切应力的影响。切应力大的单元格，其热流密度大，两个参数变化的一致性较好。

图6 各波纹通道不同单元格切应力Fig.6 Shear stress of different unit of each corrugation

3.5 典型单元格内的流动和换热特点

从上述分析可知，各单元格内换热性能的一个重要参数是其壁面切应力的大小。在此计算域的所有单元格里，最具特色的是A通道的单元格4-5和B通道的单元格4-5。A通道的单元格4-5，其切应力在各通道同单元格里最大，且比其上一单元格3-4的还要大。而B通道的单元格4-5，其切应力在各通道的同单元格里最小，且较其他通道来讲，比其上一单元格3-4的减小得最多。同时，从两片交叉堆叠的波纹板整体来看，一片波纹板的A通道单元格4-5正好与另一片波纹板的B通道单元格4-5处于同一位置，两个通道的这两个单元格正好构成一个完整的相互交叉流动影响的流动单元。故将其选作典型研究对象，对其内部表面各位置处的局部切应力和热流密度分布进行微观分析和研究。

图7为A通道单元格4-5和B通道单元格4-5的切应力分布云图。各通道单元格内的主气流均为从左向右流动，而其对应的垂直通道气流均为从下向上流动，上边附近为迎风面，下边附近为背风面。两张图比较可以看出，切应力最小的位置处于背风面及两波纹板接触节点之后，且两单元格的值都非常小，接近于0，相差并不很大。切应力最大的位置处于迎风面中间位置，但A通道单元格的值略小于B通道单元格的值。在迎风面处，由文献所知[19]，B通道上面横向A通道流出的流量相对较大，造成B通道迎风面的冲击作用大，切应力相应就会大一些，而A通道上面横向B通道流出的流量较小，A通道迎风面的切应力就没有B通道的大，所以在单元格侧面迎风面附近的切应力主要受其上面横向通道气流流出流量大小的影响，而与其通道本身的流动关系不大。

两个通道壁面切应力相差比较大的是通道中心附近，在B通道，进口附近的切应力本身就小，但到后半段，尤其是靠近背风面附近就更小了。但A通道，其进口附近处的切应力就比较大，其中间大部分区域的切应力要比B通道的大很多。尤其是在后半段靠近背风面附近，其切应力没有明显的减小。其主要的原因是，A通道的气流在单元格3-4内，由于填料侧壁面的阻挡作用，其的主流动方向发生了90°的大转弯，进入单元格4-5后，原有的主气流几乎全部转化为螺旋状前进，且速度较高，致使在近壁处的切向速度和切应力明显高于其他单元格。而B通道的气流由于受到下一个单元格5-6内填料侧壁面的阻挡作用，其在单元格4-5内的流量大大减小，流动速度减慢，壁面切应力相应即减小，尤其体现在单元格后半段。

图8为与图7对应位置的热流密度分布云图。从热流密度分布图与前面切应力分布图相比较可以看出，热流密度分布与切应力分布的规律总体来讲比较一致，热流密度和切应力具有高度的相关性。在迎风面中间位置附近，两个通道的热流密度均较大，且数值非常接近。两个通道热流密度相差比较大的是通道中心附近，在B通道，进口附近的热流密度本身就小，但到后半段，尤其是靠近背风面附近就更小了。在A通道，其进口附近处的热流密度就比较大，尤其是靠近迎风面的位置，其热流密度达到通道内的最大值，通道中间的大部分区域的热流密度要比B通道的大很多。尤其是在后半段靠近背风面附近，其热流密度没有明显的减小。由此可见，A通道因边壁的阻挡和导流作用，使其后的单元通道产生大量的横向扰动，导致壁面切应力显著增大，换热效果迅速提高。值得注意的是，两波纹板接触节点之后，尤其是在节点之后背风面的比较大一个区域，其切应力和热流密度都非常小，接近于0。这部分面积没有被充分利用，这是该波纹通道的一个需要改进的地方。

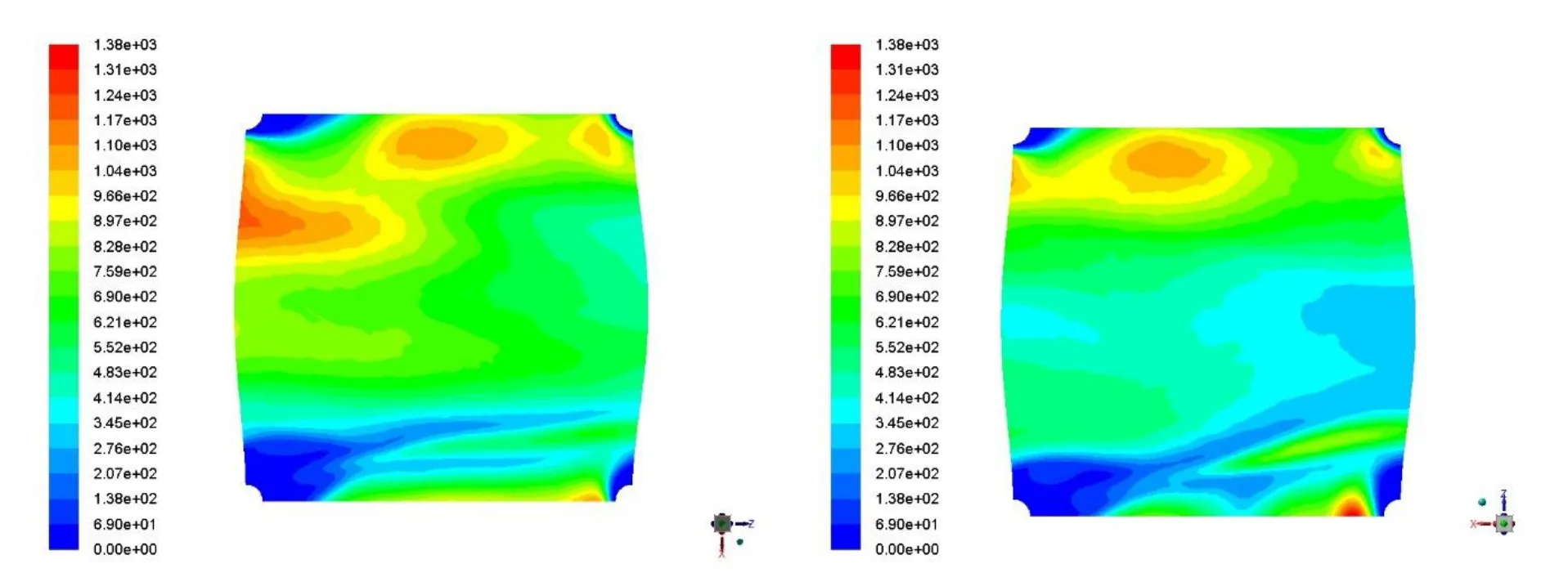
图8 A和B通道单元格4-5壁面热流密度分布Fig.8 Heat flux distribution on the wall of unit A4-5 and B4-5

4 结 论

a）各波纹通道内的温度变化相近，均为单值下降，并且开始温度下降较快，而后面温度则下降较为平缓。其中气流在侧壁受阻被完全转向90°角后，温降相对于其他通道而言明显增大。

b）沿流动方向，切应力、热流密度和气体温度逐渐下降，三者的趋势相同。切应力与热流密度具有很大的相关性。但切应力的变化更加剧烈，尤其是在气流转向90°角后，其切应力甚至比上一单元格内的切应力还大。切应力的大小主要受气流方向改变的影响。

c）即使是平均切应力和热流密度最大的单元格，在波纹通道背风面及两波纹板接触节点之后，其切应力和热流密度都很小，并接近于0。各单元格内该区域的面积相差不大，且不能忽略。这部分面积没有被充分利用，这是该波纹通道的一个需要改进的地方。

d）各单元格内热流密度差异主要是发生在主通道中间范围内，在背风面和迎风面附近相差不大。

符号说明

a—— 热扩散率，m2/sTW—— 湿球温度，K

cp—— 比定压热容，J/(kg·K)TW0——— 进口湿球温度，K

Cps—— 水的比热容，J/(kg·K)u—— 速度，m/s

Cµ——k-ε模型引入的紊动黏度经验系数u'—— 紊流脉动速度，m/s

I—— 紊流强度u0—— 进口初速度，m/s

k—— 紊动能，m2/s2δij—— 克罗内克尔符号

l—— 填料特征长度，mλ—— 导热系数，W/(m·ºC)

p—— 压力，Paμ—— 流体黏度，Pa·s

r—— 水的汽化潜热，J/kgμt—— 紊动黏度，Pa·s

Re—— 雷诺数ρ—— 密度，kg/m³

T—— 干球温度，Kρs—— 水的密度，kg/m³

T'—— 紊流脉动温度，Kε—— 紊动耗散率，m2/s3

T0—— 进口干球温度，KσT—— 紊流普朗特数