非自治Reaction-Diffusion方程的后向紧吸引子的正则性

佘连兵，张文林，李扬荣

（1.六盘水师范学院数学与信息工程学院，贵州六盘水553004； 2.西南大学数学与统计学院，重庆400715）

众所周知，拉回吸引子的紧性对研究非自治动力系统的长时间行为起着重要作用[1-5]，但这类紧性是一种片段紧性的研究，和自治系统相似，并没能展现出非自治系统对时间依赖的独特性.

最近，文献[6]对非自治动力系统所产生的拉回吸引子的后向紧性（对于过去时间的并是紧的）做了研究，并建立了完善的存在性理论，该理论指出，若系统具有一个单调递增的有界的拉回吸收集且系统是后向渐近紧的，则系统存在唯一的后向紧拉回吸引子，从此拉回吸引子的后向紧性的研究受到了广泛关注.文献[7-8]分别建立了非自治3D Navier-Stokes方程和非自治波动方程产生的非自治动力系统的后向紧吸引子的存在性定理；文献[9]运用能量的方法、高低频分解、Sobolev嵌入的方法获得了具有弱耗散非自治Schrödinger后向紧吸引子的存在性；文献[10]建立了有界域上非自治Reaction-Diffusion方程后向紧拉回吸引子的存在性定理；文献[11]研究了非自治Reaction-Diffusion方程在RN上的拉回吸引子的后向紧性.本文主要考虑如下的非自治Reaction-Diffusion方程在Lp（Q）（p≥2）空间上的后向紧动力学：

其中，λ＞0，Q是RN中的有界域，f和g的假设条件将在后面给出.

首先，在外力项g是后向λ-缓增有限的假设条件下，证明了此方程生成的动力系统在Lp（Q）（p≥2）上有一个单调递增的有界的拉回吸收集.其次，在g是后向绝对连续的假设条件下，运用一个后向截断的方法证明了该动力系统在Lp（Q）（p≥2）上是后向渐近紧的，从而由文献[6]的Theorem 2.9可知，非自治Reaction-Diffusion方程在 Lp（Q）（p≥2）上存在一个后向紧的拉回吸引子.

1 预备知识

设（X，‖·‖X）是一个Banach空间，X上有界集的全体记为 B（X）.为 X 上的 Hausdorff半距离.

定义1.1设 S（t，s）：X→X，∀t≥s是定义在X上的一族连续的映射，如果

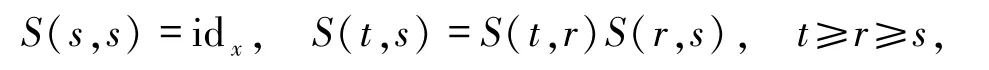
那么称S是一个非自治的过程.

定义1.2若∀t1，t2∈R，当 t1≤t2时，若 X 中非自治集 A=｛A（t）｝t∈R满足 A（t1）⊂A（t2），则称A是单增的.

定义1.3设 A=｛A（t）｝t∈R是 X 中的一个非自治集，若满足：

2）A具有不变性，即

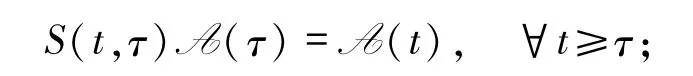
3）A具有拉回吸引性，即

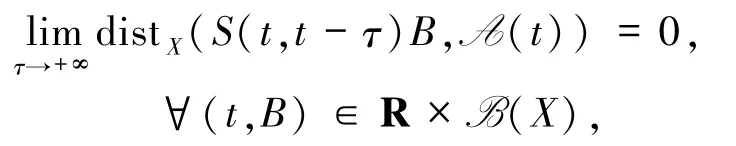
则称A是关于非自治过程S的一个后向紧吸引子.

为结果证明的需要，下面将引用文献[6]中的一个判定性定理.

定理1.1若定义X上的一个非自治过程S（·，·）满足：

（i）S（·，·）在X上存在一个单增的有界的拉回吸收集 K=｛K（t）｝t∈R；

则S（·，·）存在一个后向紧拉回吸引子

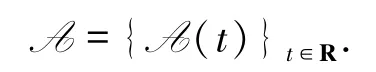
下面介绍后向Gronwall型不等式，其证明类似于文献[4]的Lemma 3.3.

引理1.1后向Gronwall型不等式：设y、y1和y2是R上的局部非负可积函数，且y′是R上的局部可积函数，b≥0是一个常数，若∀t∈R，有

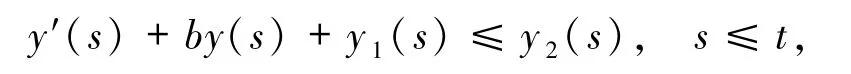
则对∀t∈R，μ＞0有

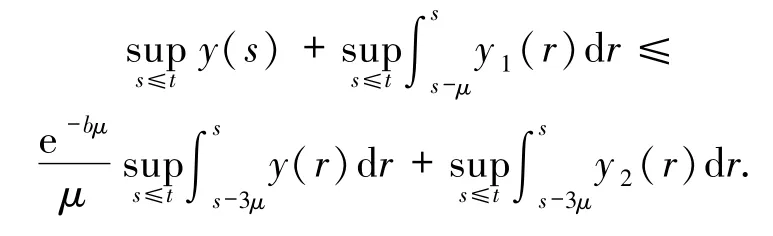
2 非自治Reaction-Diffusion方程存在唯一的后向紧拉回吸引子

考虑如下具有初边值条件的非自治Reaction-Diffusion方程

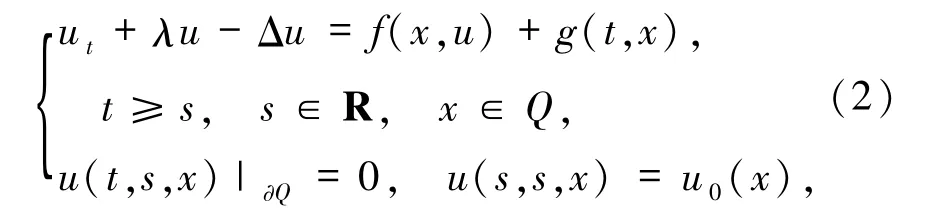
其中，λ＞0，Q是RN中的有界域，对 f和 g做如下假设：

假设 F设 p ＞2，β1，β2，β3＞0，f（·，·）∈C1（Q ×R，R）满足：

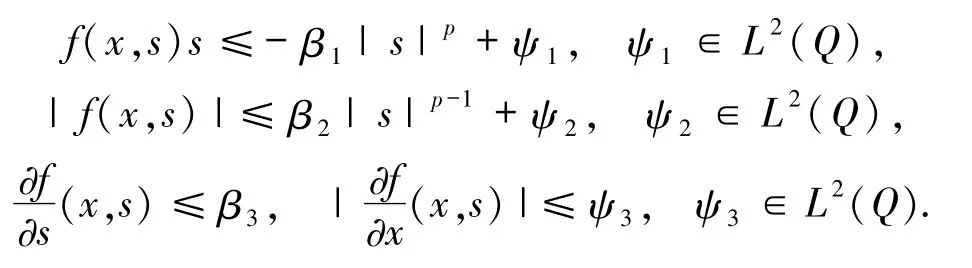
与文献[6]中对非自治项的假设条件不同，假设如下：

假设G0.

假设G1g是后向λ-缓增有限的，即其中，λ是方程（2）中给定的常数，‖·‖p（p≥2）是 Lp（Q）的范数.

假设G2g是后向绝对连续的，即

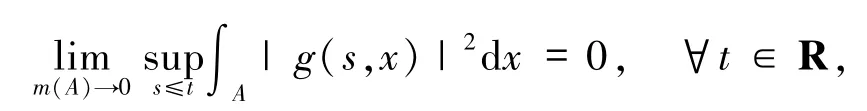
这里m（A）是集合A的勒贝格测度.

由文献[12]知，对∀s∈R，方程（2）在假设 F和假设G0下是适定的，即存在唯一的连续解

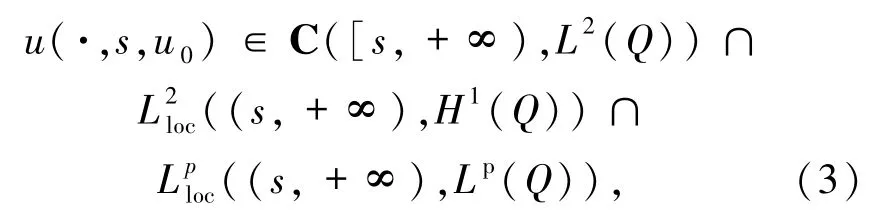
且此解关于初始值u0是连续的，故可定义如下的非自治过程

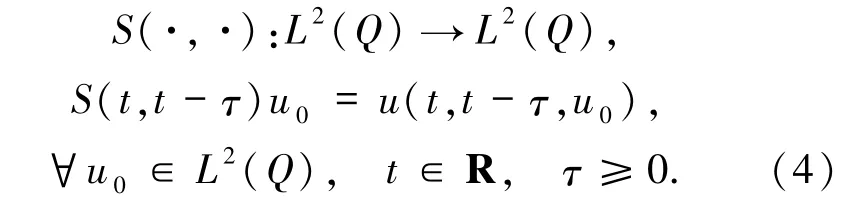
2.1 后向一致吸收性与后向截断估计先在Lp（Q）上做一个后向一致估计，为了简化计算，设c是变化的正常数.

引理2.1若假设F和假设G0、G1满足，则对于每个（t，B）∈R ×B（L2（Q）），存在一个

使得

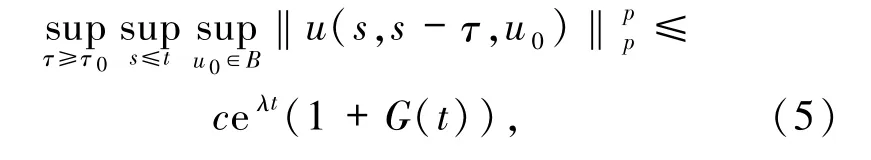
其中G（t）由假设G1给出.

2.2 本文主要结果

定理2.1若条件F和G0～G2成立，则非自治的Reaction-Diffusion方程（2）生成的过程（4），满足：

（i）在Lp（Q）中有一个单调递增的有界的吸收集 H=｛H（t）｝t∈R；

（ii）S（·，·）在 Lp（Q）中是后向渐近紧的；

（iii）在Lp（Q）中有一个唯一的后向紧拉回吸引子 A=｛A（t）｝t∈R.

证明（i）设

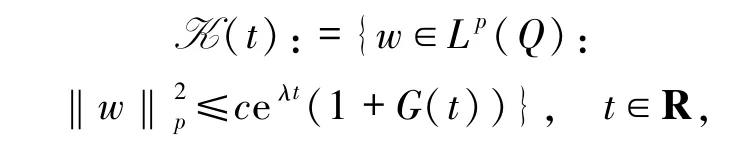
其中G（t）是假设G1中的一个增的有界的函数，故由引理2.1知K 是 S（·，·）在 Lp（Q）上的一个增的有界的吸收集.

（ii）下面证明

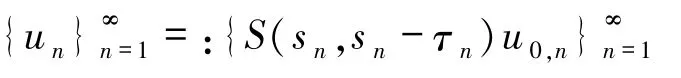
在Lp（Q）的拓扑下有一个收敛子列，这里

由引理2.2和 τn→ +∞可知存在 N1∈N和M＞0使得

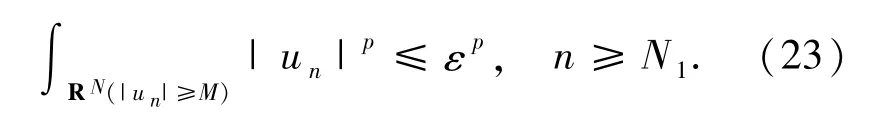
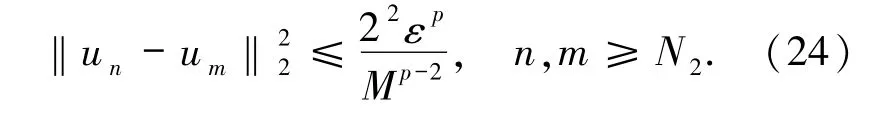
容易验证

其中

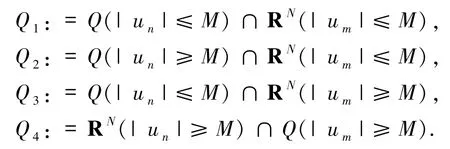
由（24）式可知

由（23）式可知：

又由

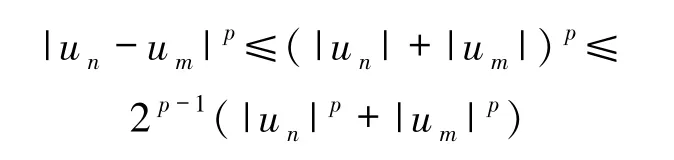
和（23）式可知

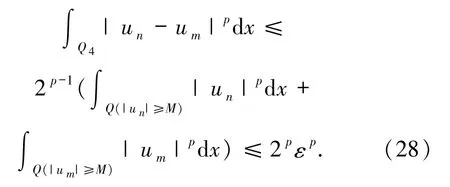
由（25）～（28）式可知

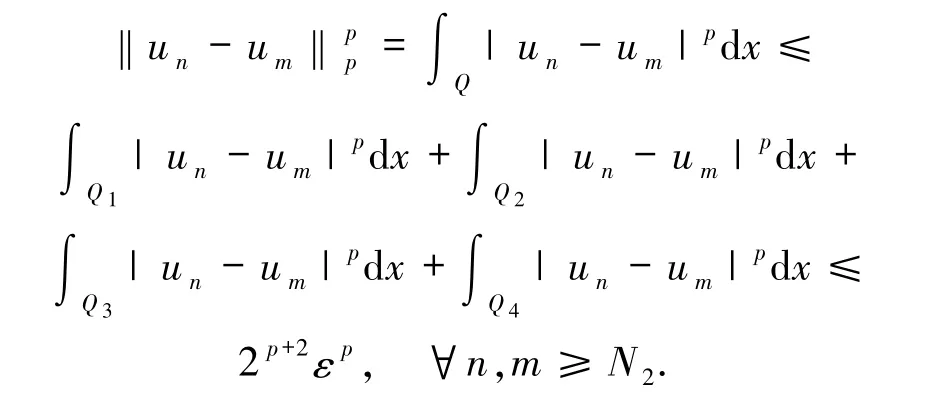
故由（i）和（ii）可知定理2.1的条件满足，所以（iii）成立.

致谢六盘水师范学院校级项目（LPSSYKYJJ201801、LPSSYKJTD201907）对本文给予了资助，谨致谢意.