Banach格上的无界绝对弱收敛的弱Dunford-Pettis算子

伯 夏，陈滋利，陈金喜

（西南交通大学数学学院，四川成都611756）

近年来，关于Banach格及其上的算子理论的研究主要是讨论算子所在的空间性质和算子本身的性质.2014年，Gao[1]详细阐述了无界序收敛并进一步进行证明；2017年，Deng等[2]详细阐述了无界范数收敛并详细进行了研究；2018年，Zabeti[3]引入并讨论了无界绝对弱收敛，Ozcan[4]提出了无界绝对弱Dunford-Pettis算子，记作uaw-Dunford-Pettis算子.本文基于弱 Dunford-Pettis算子和uaw-Dunford-Pettis算子的启发，给出了uaw-w-Dunford-Pettis算子，并研究一些相关性质.

在介绍本文之前，首先给出一些基本的概念和定理.

用E和F表示Banach格，E′和F′分别表示E和F的拓扑共轭空间.用E+表示E中所有正元素组成的集合，记作E+=｛x∈E：x≥0｝.若 E中2个元素 x和y满足｜x｜∧｜y｜=0，那么称x和 y是不交的，记作x⊥y.如果满足对E中任意的非空有上界的集合有上确界，那么E具有Dedekind完备.相似的，如果满足对E中任意的非空有上界的可数集合有上确界，那么 E具有 δ-Dedekind完备.如果｛xα｝⊂E，若对∀x′∈X′，有x′（xα）→x′（x），则称xα弱收敛到 x，记作.如果｛xα｝⊂E，若对∀μ∈E+，都有，那么就称xα无界绝对弱收敛到零，记作.对任意 x∈E，如果x≥0，有T（x）≥0，那么称 T是正算子；如果T=T1-T2，且T1、T2是正算子，则称 T 是正则算子.如果

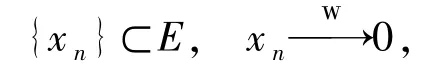
有‖T xn‖→0，那么称T是Dunford-Pettis算子.T：E→X是一个连续算子，X是Banach空间，若对于E中的每一个范数有界不交列｛xn｝，都有‖T xn‖→0，那么就称T是M-弱紧算子.

未解释的有关Banach格和算子理论的一些概念、术语及符号详见文献[5-6].

1 uaw-w-Dunford-Pettis算子的相关性质

文献[4]中提出了无界绝对弱Dunford-Pettis算子，记作uaw-Dunford-Pettis算子.如果范数有界列，有‖T xn‖→0，那么称 T是uaw-Dunford-Pettis算子.文献[5]中提到一类算子——弱 Dunford-Pettis算子.如果｛xn｝⊂E，′，若，有，则称T是弱Dunford-Pettis算子，并在文献中对弱Dunford-Pettis算子进行了详细研究.结合uaw-Dunford-Pettis算子和弱Dunford-Pettis算子的定义，本文提出新算子uaw-Dunford-Pettis算子.

定义1.1设E和F为Banach格，T：E→F是一个有界线性算子.若对E中任意范数有界列xn，fn∈F′满足，有fn（Txn）→0，则 T是uaw-w-Dunford-Pettis算子.

例子 1.2考虑 S：C[0，1]→l∞是一个正算子，定义为

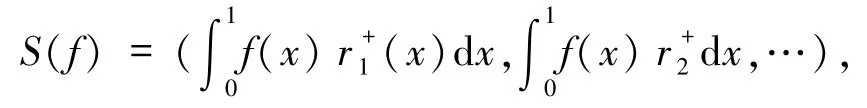
其中 f∈C[0，1]，｛rn｝是一列定义在[0，1]上的Rademacher函数列.设fn∈C[0，1]是一个范数有界的不交列且，由文献[3]定理7 有.又因为 C[0，1]有 Dunford-Pettis性质，因此，S 是一个uaw-w-Dunford-Pettis算子.

定理1.3设T：E→F是从Banach格E到Banach格F的正的有界线性算子，若E′具有序连续范数，那么下列条件等价：

1）T是一个uaw-w-Dunford-Pettis算子；

2）在E中任意的无界绝对弱零列｛xn｝和在F′中任意不交的弱零列｛fn｝，有fn（T（xn））→0.

证明1）⇒2） 显然成立.

2）⇒1） 利用反证法证明.首先假设T不是uaw-w-Dunford-Pettis算子，那么就有无界绝对弱零列｛xn｝⊂E 和弱零列｛fn｝，满足fn（T（xn））0，即∃ε ＞0，对∀N ＞0，∃n（n＞N），使得

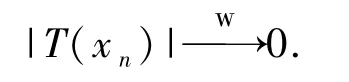
因此，令n1=1，有4 fn1（｜T（xn）｜）→0，则可以找到n2＞n1有.假设k被选定，有.因此，当nk+1＞ nk时有

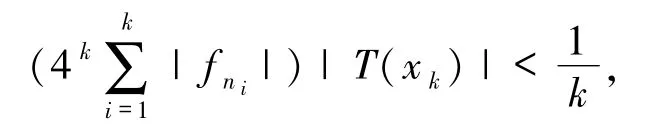
所以能找到｛xn｝的一个子列｛yn｝和｛fn｝的一个子列｛gn｝，对任意的 n≥1，满足

和

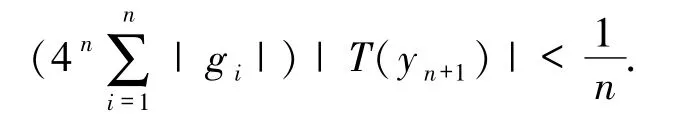
根据文献[5]中引理4.35，可以构造如下不交列：

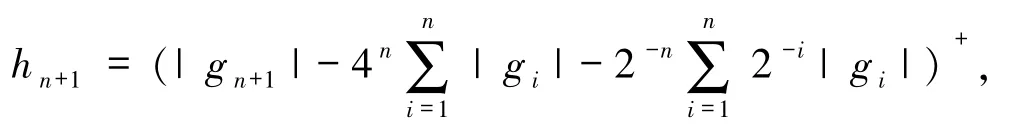
显然有hn+1是F′中不交的弱零列，并且有

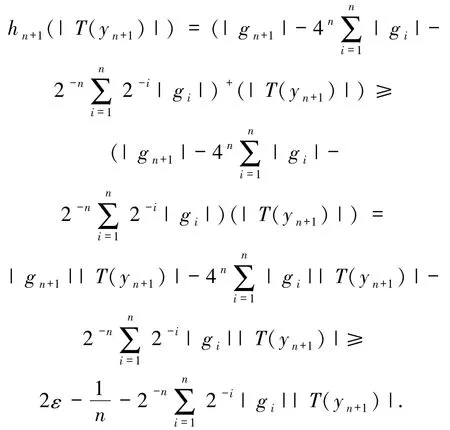
故当 n 充分大时，得到hn+1（｜T（yn+1）｜）≥ε

由文献[5]定理1.23知

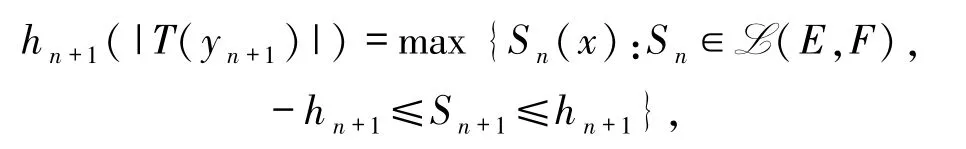
那么存在sn+1∈F′使得 -hn+1≤sn+1≤hn+1，且sn+1（T（yn））≥ε，由hn+1是不交的弱零列，故sn+1是不交的弱零列，这与条件（2）相矛盾.因此结论成立.

定理1.4设E、F是Banach格，T：E→F是一个正uaw-w-Dunford-Pettis算子，那么在E+中任意范数有界不交列｛xn｝和在F′中任意的弱零列｛fn｝有

证明假设｛xn｝是E+中任意的不交列，那么可以得到对∀ε＞0和∀f∈V，∃0≤g∈F′和 k∈N，当 n＞k时，有

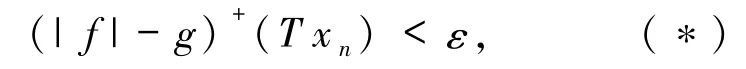
采取反证法来证明（*）.首先假设（*）是错误的，那么就有∃ε′＞0，对∀0≤g∈F′和∀N，至少∃一个 k（k＞ N），使得（｜fk｜-g）+（T xk）≥ε′.因此，设 g=4｜f1｜和n1=1，那么就∃一个n2（n2＞n1），使得

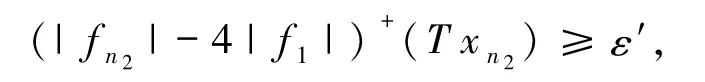
同样地，设

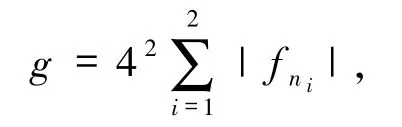
那么就∃一个n3（n3＞n2），使得

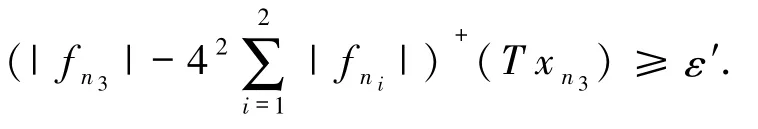
通过数学归纳法，可以找到一个严格单调递增的数列｛nk：k∈N｝，满足

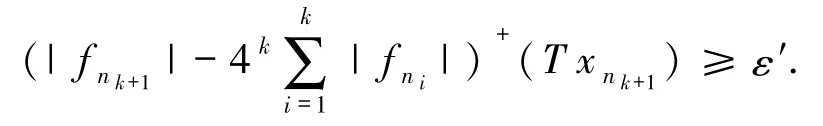
令

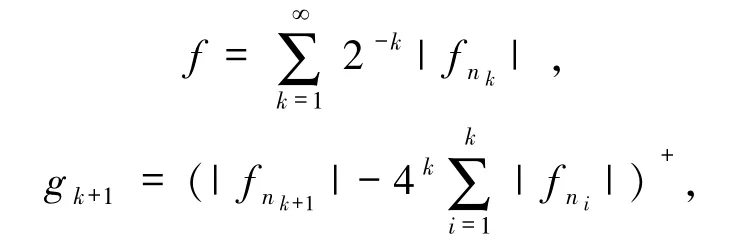
然后根据不交列的构造技巧，设

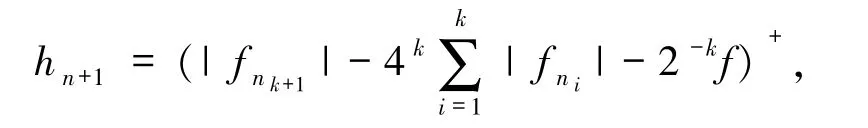
由文献[5]引理4.35知，｛hn+1｝是一个不交列.由文献[5]定理4.34 知，在F′中.由条件知｛xn｝是任意的不交列，那么通过文献[3]引理2知，再由文献[3]引理1 知.因为T是一个uaw-w-Dunford-Pettis算子，所以有hn+1（T xnk+1）→0.但是，有 0≤gk+1≤hn+2-kf，所以

因此，矛盾.所以命题（*）是正确的.

现在设0≤g∈F′和任意N满足（*）.因此，当n＞N时有

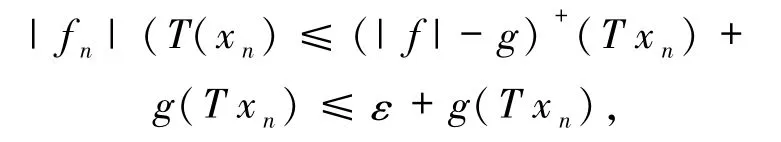
定理1.5设E、F是Banach格，T：E→F是一个正uaw-w-Dunford-Pettis算子，若F是Dedekind 完备.那么 S：E→F，其中

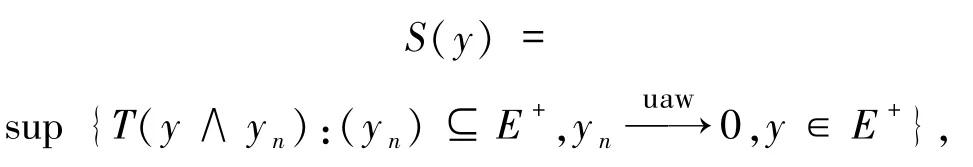
有Kantorovich延伸算子且也是一个uaw-w-Dunford-Pettis算子.

证明设 x，y∈E+，，ξn∈E+，那么有

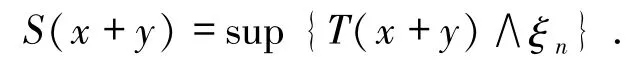
由文献[6]定理6.5知

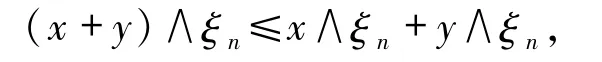
所以有

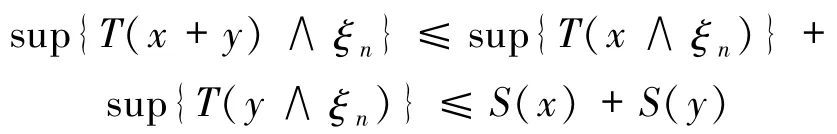
和

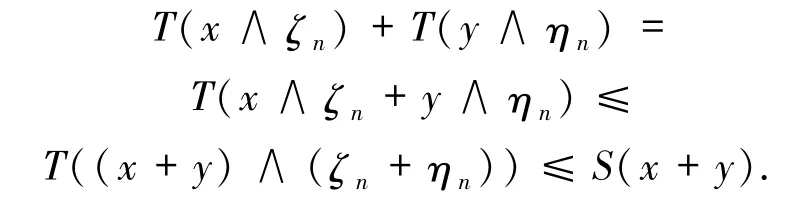
左边取上确界，所以有

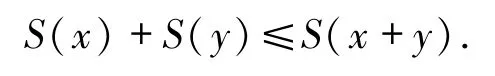
因此，S（x）+S（y）=S（x+y）.由文献[5]定理1.10知，S（x）有一个唯一的Kantorovich延伸算子.接下来证明 S（x）是一个 uaw-w-Dunford-Pettis算子.设

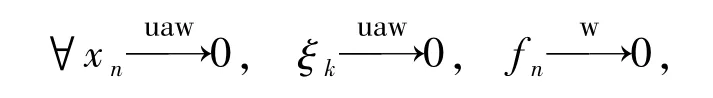
且xn，ξk∈E+，fn⊂F′，那么有

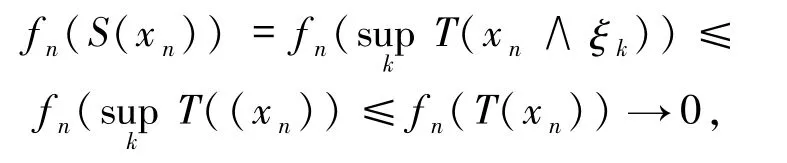
因此，S（x）是一个 uaw-w-Dunford-Pettis算子.

2 与相关算子之间的关系

定理2.1设 E、F是 Banach格，若E′有序连续范数，那么每个弱Dunford-Pettis算子T：E→F是一个uaw-w-Dunford-Pettis算子.

证明设｛xn｝是E中任意范数有界列，并且，由文献[3]定理7 知，又由于T是一个弱Dunford-Pettis算子，那么有对，使得fn（T（xn））→0 成立.故结论得证.

定理2.2设T是从Banach格E到Banach格F的uaw-w-Dunford-Pettis算子，若F有序连续范数，则T是M-弱紧算子.

证明设｛xn｝为E中范数有界的不交列，由文献[3]的引理2知，又因为T是uaw-w-Dunford-Pettis算子，知道｛T（xn）｝是 F 中的 Dunford-Pettis集.因为F有序连续范数，那么就有｛T（xn）｝是紧集.另一方面，｛T（xn）｝是 F 中的弱零列，因此有｛T（xn）｝依范数收敛到零.所以，T把E中范数不交列映为范零列，故 T是 M-弱紧算子.