基于C 语言的逆矩阵求解实现机理探究

岳毅然

（中山大学 智能工程学院，广东 广州510275）

矩阵是理工科数学中一个重要的概念，它是代数领域的主要研究对象，也是数学理论研究和结合应用的一个重要工具。十九世纪中叶，英国数学家西尔维斯特为了将数字的矩形阵列区别于行列式而发明了“矩阵”一词[1]。

矩阵的应用非常广泛，它不仅被应用于数学领域里，在传统理学、力学、现代自然科学、工程技术、计算机科学以及社会科学等诸多领域都是一个重要的工具。

如图像的数据化表示中，图像在计算机中以矩阵的形式进行存储和读写，也通过对矩阵进行运算和变换等操作实现对图片的处理。

逆矩阵作为矩阵论的一个重要分支，它在工程数学上如解线性方程组等等的应用非常广泛。

为了更好地在实际问题中求解矩阵的逆矩阵，本文根据逆矩阵的定义和性质总结了一种适合计算机语言求逆矩阵的方法，帮助我们更快更准地解决人工计算量较大的求逆矩阵问题。

1 数学理论基础

设A 是数域上的一个n 阶矩阵，若在相同数域上存在另一个n 阶矩阵B，有AB=BA=E，则称B 是A 的逆矩阵，而A 被称为可逆矩阵。

通常来讲，计算机求解逆矩阵的常规方法为伴随矩阵法，其数学理论基础如下。

首先，n 阶矩阵A=[aij]为可逆的充分必要条件为A 是非奇异矩阵，故有：

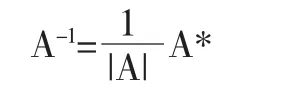
其中|A|为矩阵A 的行列式的值，A*称为伴随矩阵，其各元素Aij由矩阵A 各元素的代数余子式组成：

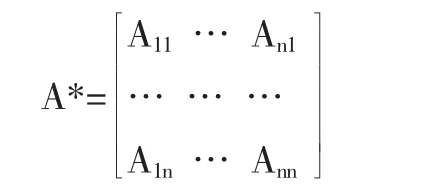
当矩阵A 的行列式|A|为零时，该矩阵没有逆矩阵（即分母不能为0）。

伴随矩阵A*的元素与原矩阵A 的元素的下标是转置关系，可以根据求解代数余子式（即行列式）功能函数和双重循环矩阵赋值的方式生成伴随矩阵，从而实现矩阵求逆功能。

这种求逆矩阵的方法要求解得矩阵A 的行列式|A|及A 的伴随矩阵A*，人工计算量较大，但是计算程序和循环较为简单，适合计算机运算，故在理论上具有重要的地位。

1.1 矩阵行列式求解

设A 为一个n 阶矩阵，可以采用列主元高斯消去法，经过p次行交换或列交换将矩阵A 转化为上三角矩阵，后根据：

求得矩阵行列式的值。

手动求解时用上述方法较为简便，但在计算机语言程序设计中，为解决更多维的矩阵行列式问题，则倾向于使用按行展开的方法。

矩阵的行列式等于它的任一行（列）的各元素aij与其对应的代数余子式乘积之和，即：

1.2 伴随矩阵求解

设一个n 阶矩阵A，将矩阵A 中的元素aij所在的第i 行和第j 列元素划去后，剩余的各元素按原来的排列顺序组成的n-1 阶矩阵所确定的行列式称为元素aij的余子式，记为Mij，称Aij=（-1）i+jMij为元素aij的代数余子式。

由矩阵A 的各代数余余子式Aij组成一个新矩阵，被称为矩阵A 的伴随矩阵，记为A*。

2 程序设计和实现细节

在较为成熟的理论研究基础之上，各类软件常作为载体用以实现各类运算，提高了信息处理的效果与效率，为人们对信息所进行的处理提供了便利。常见的有matlab、SPSS、C/C++、Excel 等，本文基于C 语言对求逆矩阵的实现过程与机理进行详细介绍。

全过程从三个方面展开：求解行列式函数、求解伴随矩阵函数、主函数。

2.1 函数getA_value：行列式

利用矩阵的按行展开方法求解行列式的值。输入为欲求矩阵和行数，后经三重循环，遍历各元素，后将各项相加得到行列式的值。

详细实现细节如下所示。

2.2 函数getA_star：伴随阵

为求解伴随矩阵，需要借鉴上一getA_value 函数的求解代数余子式部分，同样借助for 循环遍历矩阵各元素和伴随矩阵各元素，而后组成伴随矩阵。

2.3 主函数main：程序实现

如图1、2、3 所示，测试每个函数和模块，验证基本功能的准确性，并对整个程序进行黑盒测试，程序良好运行。

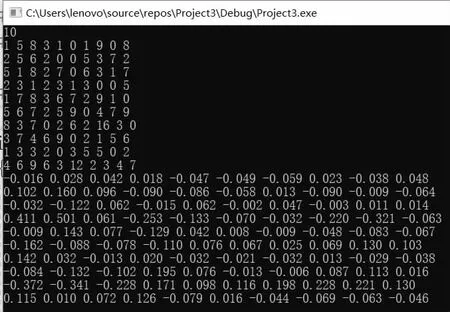
图1 测试案例1

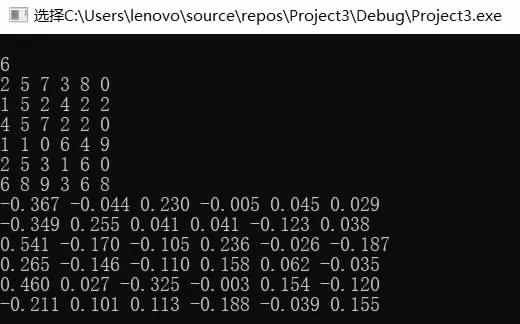
图2 测试案例2

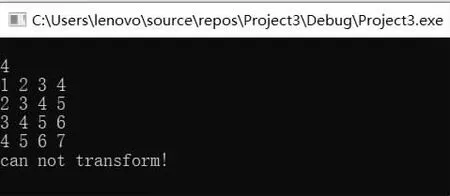
图3 测试案例3

3 结论

本文基于C 语言实现了求解任意阶数方阵的逆矩阵的任务。算法逻辑清晰简洁，融合了高等数学、线性代数等数学基础概念与结构化程序设计理念，主要应用的数学知识有行列式降阶展开定理、伴随矩阵定义以及（代数）余子式定义等，为日后包括图像处理与分析、数据挖掘和处理、工程数学等领域提供了理论和实践基础。