两个非线性发展方程的精确解

冯立婷 孙轶男 徐晓明

（东北大学，辽宁 沈阳110004）

近年来，非线性科学飞速发展，许多非数学领域的现象可通过非线性方程的模型进行描述。因此，国内外众多学者对于求解非线性方程进行了深入的研究[1-2]。随着计算机科学的发展，求解非线性方程的精确周期解变得更加简便。本文对于mKdV 方程[3-4]、KP 方程[5-6]通过修正映射法、拓展Jacobi 椭圆函数展开法进行研究，证明了两种方法的有效性。

1 mKdV 方程的修正映射法

修正的Korteweg-de Vries 方程（以下简称mKdV 方程）

其中α 为自由参数。此方程在描述等离子的孤立子模型中具有重要作用。

假设mKdV 方程的行波解具有形式

经过行波变换，对φ（ξ）积分一次并取积分常数为0，可得

设方程具有以下形式的孤立波解

根据其次平衡原则，平衡方程（16）中线性最高阶导数项与最高阶非线性项，即m+3=3m+1，可确定孤立波解的阶数m=1，于是方程（16）具有以下形式的解析近似解：

其中A0，A1，B1待定。根据修正的映射法，假设f 满足下列方程：

也即

结合（19）、（20）式，可得

带入（16）式，整理各次幂系数并令其为零，可以得到以下非线性代数方程组：

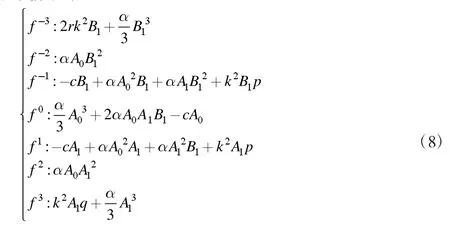
通过Maple 或Mathematica 软件，可解得

将以上解带入式（18），可得

当m→1 时，得到解：

③当f（ξ）=cn（ξ）时，p=2m2-1，q=-2m2，r=1-m2

当m→1时，得到解：

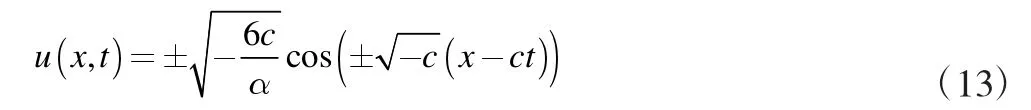
本章根据修正的映射法，对mKdV 方程为例，基于齐次平衡原则，求得了经典的孤立波解，对分析此类非线程方程描述的物理现象有积极作用。经过计算，修改的映射法还可以用于其他形式的非线性方程的求解。

2 Kadomtsev-Petviashvili 方程的拓展Jacobi 椭圆函数展开法

Kadomtsev-Petviashvili 方程（以下简称KP 方程）

其中α，γ，ε 为自由参数。此方程可以视为KdV 方程在高维情况下的推广。

假设KP 方程的行波解具有形式

经过行波变换，对φ（ξ）积分两次并取积分常数为0，可得

设方程具有以下形式的孤立波解

其中f（ξ）=sn（ξ），g（ξ）=cn（ξ）。根据其次平衡原则，平衡方程（15） 中线性最高阶导数项与最高阶非线性项，即m+2=2m，可确定孤立波解的阶数m=2，于是方程（15）具有以下形式的解析近似解：

其中a0，a1，a2，b1为待定系数。根据Jacobi 椭圆函数的性质，求得：

将上式带入（15），根据Jacobi 椭圆函数的关系，将（18）中gj（j=2，3…n）转化为fi（i=1，2，…，n）的多项式，并令figi，（i=1，2，…，n；j=0，1）的系数为零，可得到方程组

当m→1 时，通过Maple 解以上方程组，可得以下情况：

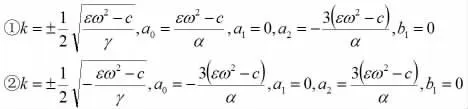
下面分析各解的具体情况：

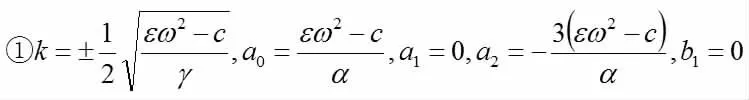
拓展的Jacobi 椭圆函数展开法借助Maple 软件得到了如（21）-（22）的系列解析近似解，与参考文献中已知使用混合指数方法得到KP 方程的解一致。相比较可知，拓展的Jacobi 椭圆函数展开法更为简便，并可用于其他形式的非线性方程的求解。