基于逆动力学的机械臂鲁棒位置控制方法的设计

段 纯，顾建华

（1.安徽新闻出版职业技术学院机电信息系，安徽合肥230601；2.盐城工业职业技术学院机电工程学院，江苏盐城224005）

随着科学技术的不断进步与国民生活水平的不断提高，人们对工业的要求也越来越高。机械臂的出现为工业智能化的发展提供了良好动力。机械臂通过对人类的手臂进行模仿，能够通过编程使其完成指定的货物抓取、搬运以及操作简单的劳动工具等功能[1]。机械臂在工业上可完成繁重具有循环性的工作，同时机械臂还能够在较为恶劣的环境下进行工作，从而减轻了人们的劳动量，降低了人们在恶劣环境下工作发生危险的系数[2]。由于机械臂的独特优势，近些年来机械臂已被广泛应用于轻工冶金、煤炭及矿产开采、快递物流等多个技术领域。机械臂在运动过程中的位置控制，决定着机械臂工作过程的准确以及稳定性。若机械臂在位置控制过程中准确度较低，波动性较大，将会严重影响机械臂的性能[3]。因此，对机械臂的位置控制进行研究就变得意义非凡。

伴随着研究人员对机械臂位置控制的不断深入，当下出现了多种多样的机械臂位置控制方法。例如，Van等[4]通过对神经网络方法进行研究，提出了一种基于径向基函数（RBF）的自适应轨迹跟踪神经网络控制方法，对N连杆机器人的关节位置控制问题进行了RBF网络控制，利用反向传播算法和李雅普诺夫稳定性定理，推导了网络参数的自适应转向规律，保证了整个系统的稳定性和权值自适应的收敛性。Lu等[5]提出了一种基于线性二次型调节器（LQR）的机械臂位置控制的方法，利用假设模态法和拉格朗日方程，建立了机械臂的动力学模型，利用动力学模型推导出状态方程，基于Mamdani模型，在传统的LQR控制中加入模糊算法，对LQR控制变量R进行自适应调整，提高了控制系统的适应性。Oliveira等[6]提出了一种基于混沌的机械臂高阶滑模位置控制优化算法，对机器人关节空间位置控制的高阶鲁棒滑模控制器的参数进行优化，进而实现位置的控制。Wang等[7]设计了一种基于混合控制的机械臂定位与振动控制方法，利用参考值的幅度约束构建延时滤波器，利用延时滤波器建立混合闭环控制系统，对机械臂的位置进行控制。上述方法虽然都能够对机械臂的位置进行控制，但控制过程较为缓慢，而且准确性与鲁棒性都不高。

对此，本文以反演控制方法与滑模控制方法为基础，提出了基于逆动力学的机械臂鲁棒位置控制方法。通过对机械臂电机系统的动力学进行分析，获取电机系统的动力学函数，明确了电机系统的动力学控制过程。利用转矩到位置转换方法和反演滑模控制方法设计了逆动力学控制器，通过反演滑模控制方法对调节变量的李雅普诺夫函数及其导数进行分析，获取电机转矩函控制函数。通过转矩到位置转换方法，将利用电机转矩求取的位置控制量传入伺服电机，实现对机械臂位置的快速准确、鲁棒的控制。实验结果显示，所提方法能够较好地对不同激励信号产生的目标轨迹进行追踪，说明所提方法不仅能够对机械臂的位置进行准确快速的控制，而且还具有较强的鲁棒性。

1 系统描述

本文所采用的伺服电机为埃斯顿公司的EMJ-04APB22型电机，该电机的参数如表1所示。伺服电机系统通常依靠反馈增益从电机轴上获取所需的输出信息。比例(P)-积分(I)-微分(D)控制器由于其设计以及实现过程相对较为简单，为伺服系统中最常用的一种用于获取反馈增益的控制器。由于在EMJ-04APB22型电机内部，比例(P)运算起主要作用，因此，可假设伺服电机系统的内部控制器为P型控制器。通常利用该低电平控制器的输出，作为电机转矩控制的控制信号，以通过对电机转矩的控制实现对机械臂的运动过程进行调节。

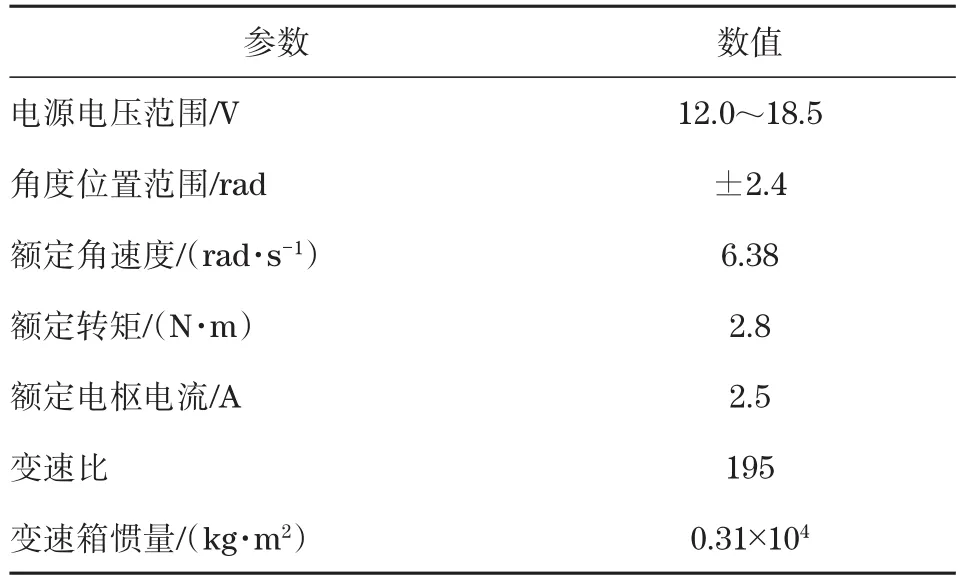
表1 EMJ-04APB22型电机参数表Tab.1 Motor parameters of EMJ-04APB22

在忽略电机的电气动力因素下，令齿轮轴的速度和加速度分别为与，电机传动比为kg，电机的阻尼系数为B，则电机系统动力学函数可以表示为[8]

电机动力学的简化框图如图1所示。图中：ωm，ω分别表示电机轴转速与变速箱的速度输出；kp表示控制器的p增益量；qd，q分别表示电机的目标位置与实际位置，追踪误差e=qd-q。因此，低电平P型控制器输出Δq的求取过程为

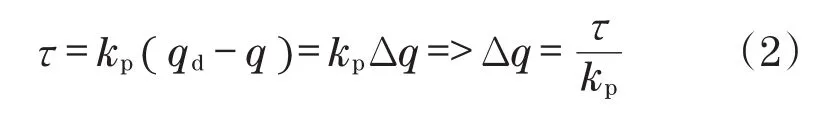
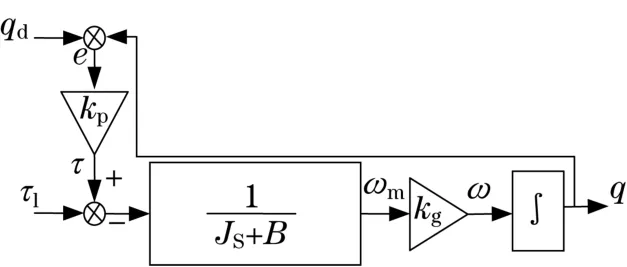
图1 电机动力学简化框图Fig.1 Simplified block diagram of motor dynamics

2 控制器设计

如图2所示，本文利用转矩到位置转换方法和反演滑模控制方法设计了一种逆动力学控制器，用以实现机械臂对目标位置qd进行准确的追踪。

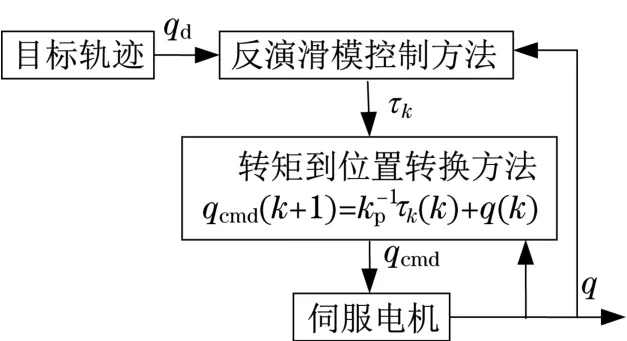
图2 逆动力学控制器设计框图Fig.2 Design block diagram of inverse dynamics controller

2.1 反演滑模控制方法设计

为了克服机械臂系统中存在的外界噪声干扰以及时变不定性、建模误差等因素，在此将滑模控制方法与反演控制方法相结合，设计了一种反演滑模控制方法[9]。

令调节变量z1为

则调节变量z1对应的李雅普诺夫函数V1及其导数为

利用调节变量z1设计虚拟控制量a1为

式中：c1为大于零的常量系数。

通过虚拟控制量a1定义调节变量z2：

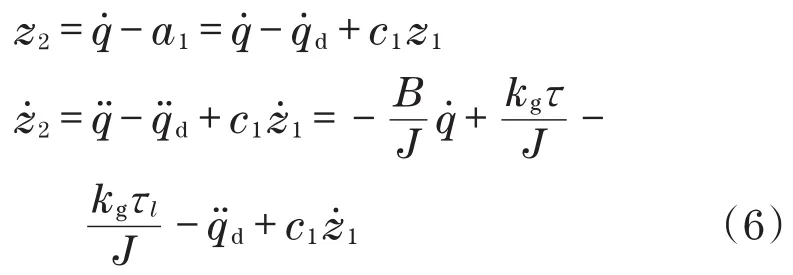
利用调节变量z2对进行变形可得

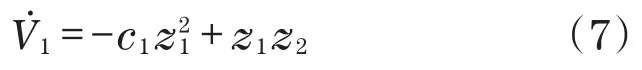
将调节变量z2视为滑动变量s：

则调节变量z2对应的李雅普诺夫函数V2及其导数为

联合式（6）、式（8）及式（9）可得出电机转矩控制函数为

式中：c2＞0，k＞0为常量系数；sign(s)为符号函数，

式中：η为有界干扰量。当，k＞ |η|时，可保证为负定，此时系统便处于稳定状态。

根据系统动力学函数式（1），可得t时刻与t-L时刻干扰转矩τl的表达式[10]为

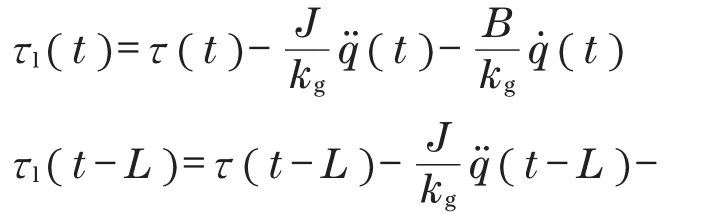
式中：L＞0是一个时间较短的采样时间；由于参考轨迹具有光滑性，Jkg与Bkg为常量，机械臂关节具有有界速度和加速度，因此，可以假定为光滑函数。

则在一个短的采样时间内，

在较短的采样时间内，τl(t)-τ(t-L)引起的微小误差可忽略不计。此时，关节加速度可使用关节位置测量数据的可靠精确微分器进行估算[11]。

2.2 转矩到位置转换方法设计

如图2所示，转矩到位置转换方法将利用式（10）求得的电机转矩τ来获取一个位置控制量qcmd。由于式（10）求得的电机转矩τ与伺服系统中低电平P型控制器产生的转矩应相等，因此，具有如下表述[12]：

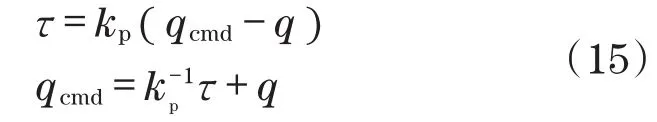
令采样时间为Ts，则第k+1次采样时所得的位置控制量qcmd[k+1]为

由此可见，第k+1次采样时所得的位置控制量qcmd[k+1]，需要通过第k次采样时的电机转矩以及电机实际位置来确定。将确定后的位置控制量qcmd[k+1]送入伺服电机，以获取对机械臂的位置控制结果q，从而实现电机转矩到机械臂位置的转换控制。

3 实验结果与分析

为了验证所提方法的轨迹追踪性能，通过Matlab/Simulink软件进行了仿真实验。实验中分别采用了阶跃信号以及梯形信号、正弦波信号来产生目标轨迹，并用所提方法及P型控制器方法对这两种目标轨迹的追踪轨迹进行了测试。实验中设定常量系数c1=45，c2=280，k=12，低电平 P 型控制器的比例增益kp=35，干扰转矩τl为

式中：mc=80.3×10-3N·m为静摩擦系数；dc=15×10-3N·m为库仑摩擦系数；hc=3.8×10-3N·m为黏性摩擦系数。

不同方法对阶跃信号产生的目标轨迹的追踪效果如图3所示。由图3可见：所提方法及P型控制器方法都能完成对目标轨迹的追踪，但是将这两种方法产生的追踪轨迹进行对比发现，所提方法的追踪轨迹比P型控制器方法的追踪轨迹更为稳定，且能够更快地完成目标轨迹的追踪。不同方法对梯形信号产生的目标轨迹的追踪效果如图4所示。通过对图4中不同方法的追踪轨迹进行对比可见，图4（a）的追踪轨迹波动性较大，而且波动的最大幅度也较大，对目标轨迹的追踪速度较慢。图4（b）的追踪轨迹中波动性较小，而且波动的最大幅度也较小，能够更快地完成目标轨迹的追踪。图5为不同方法对正弦波信号产生的目标轨迹的追踪效果。将图5中不同方法的追踪轨迹进行对比可见，图5（a）的追踪轨迹过冲量较大，而且过冲次数较多，产生的追踪轨迹波动次数较多，当产生过冲时，对过冲量的调节时间较长。图5（b）的追踪轨迹中不仅过冲量较小，而且过冲次数较少，当产生过冲时，能够较快地对过冲量进行调节，使追踪轨迹能够更快地到达目标轨迹。由此可见，所提方法对目标轨迹的追踪效果较好，追踪过程更为快速、稳定。说明了所提方法能够较快、较稳定地对机械臂的位置进行较准确的控制。

图3 阶跃信号产生的目标轨迹追踪效果Fig.3 Effect of step signal on target trajectory tracking

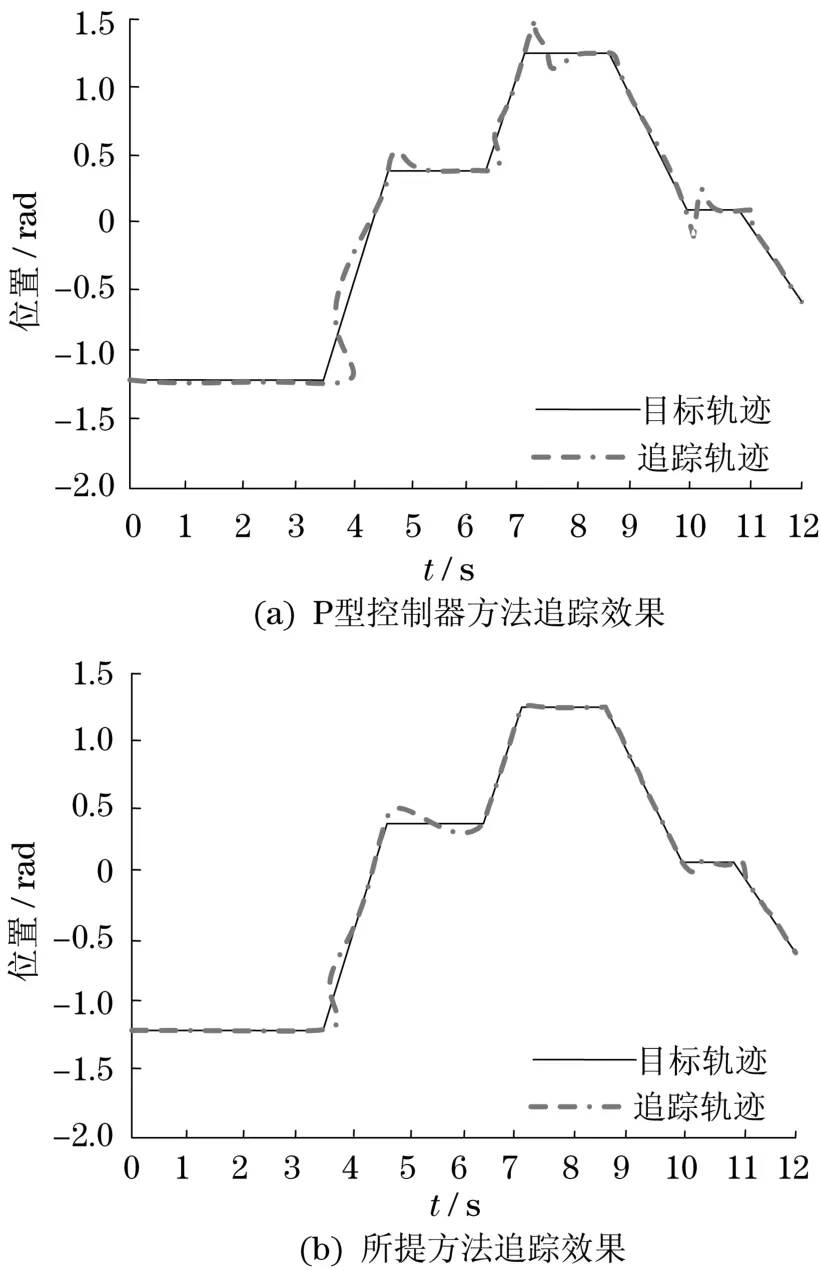
图4 梯形信号产生的目标轨迹追踪效果Fig.4 Effect of target trajectory tracking by trapezoid signal produces

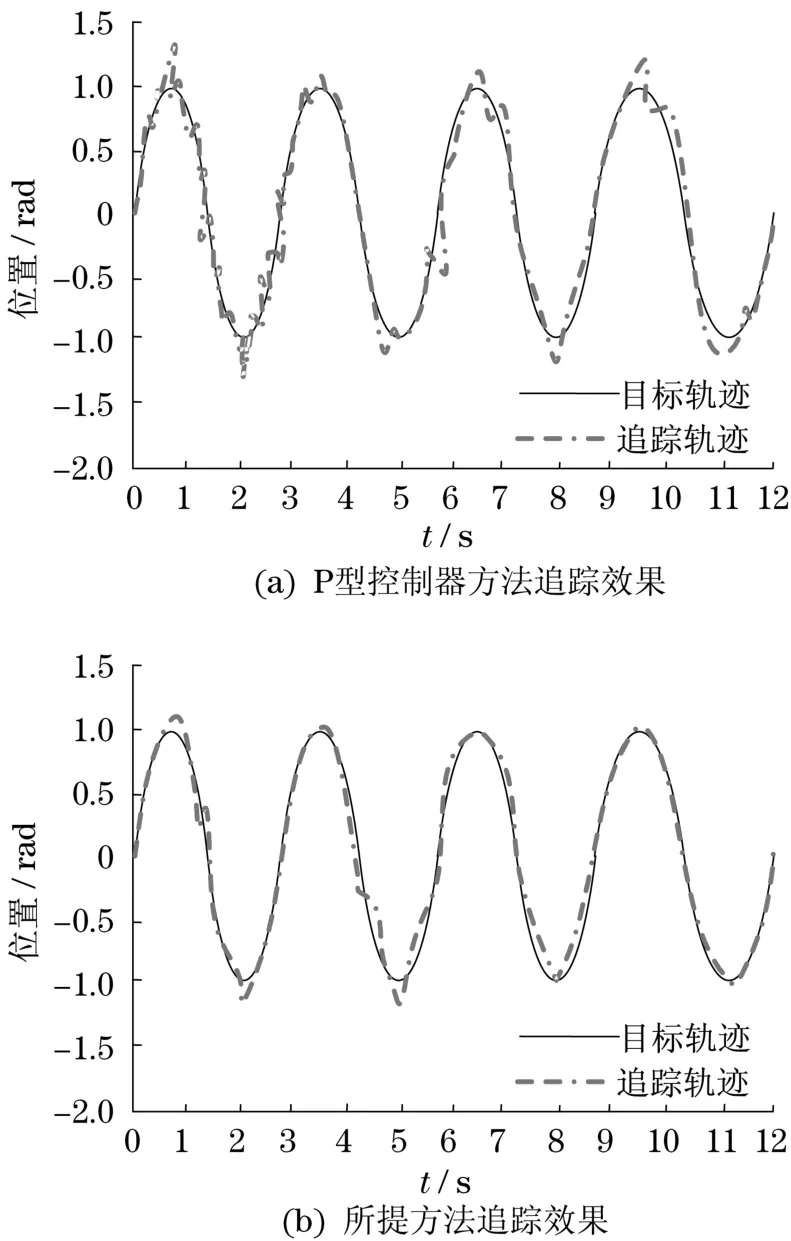
图5 正弦波信号产生的目标轨迹追踪效果Fig.5 Effect of target trajectory tracking by sine wave signal

4 结语

本文对机械臂的电机系统进行了分析，获取了机械臂电机系统的动力学函数。在此基础上设计了基于逆动力学的机械臂鲁棒位置控制方法。通过联合反演滑模控制方法与转矩到位置转换方法，设计了逆动力学控制器。该控制器通过将反演控制方法与滑模控制方法相结合，以抵御外界噪声以及时变不定性、建模误差等因素干扰，通过构造电机转矩函数，求取电机转矩。利用转矩到位置转换方法，以电机的转矩为依据，求取电机的位置控制量，并将该控制量送入伺服电机，用以完成对机械臂的准确、快速以及稳定的控制。并在实验中利用所设计方法对多种激励信号产生的位置轨迹进行了追踪，追踪结果显示，所设计方法不仅能够快速、准确地对目标轨迹进行追踪，而且追踪过程较为平稳。说明所设计方法能够对机械臂进行准确且鲁棒的位置控制。