假设策略在小学数学解题中的应用
江苏省扬州市邗江区黄珏学校 郑淑敏
小学生对抽象问题的理解有一定难度。在面对此类数学问题时,学生在思考解答时总是觉得缺少这样或那样的条件,因此无法理清思路,找不到突破口而束手无策。受陶行知先生“接知如接枝”的启发,本文重点阐述假设策略在小学教学中的应用。引导学生以假设为“枝”,将抽象问题直观化、具体化,从而化难为易,化繁为简,达到“接知”的目的,使学生很快地找到解决问题的突破口,进而巧妙地解决一些问题,激发学习兴趣,提升学习数学的信心。
一、特例假设,由特殊到一般解决问题
在小学数学教学中,经常会遇到一些题目只告诉两个量的某种关系,却要判断这两个量的大小关系或求这两个量的比或者比值。比如:
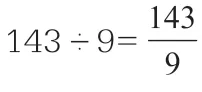
由两个例题可以发现,当求的是“比”时,可充分运用“特殊值法”进行假设来解决问题。这样把未知的、不确定的量进行假设,使未知变已知,轻松解决问题。
二、同质假设,解决“鸡兔同笼”问题
“鸡兔同笼”问题,可以说是古今数学中利用假设策略解决的经典问题。现在也当属苏教版小学数学应用假设策略的重中之重。
例3:鸡兔同笼,头共8 个,脚共22 只,问:鸡、兔各几只?
在教学实践中,教师可以通过画图(如下图)来引导学生快速地找出正确的答案:画8 个圆圈代表8 只动物,假设全是鸡,需要画8×2=16 只脚,还需要再画22-16=6 只脚,而一只兔比一只鸡多2只脚,因此再画时每只鸡加2 只脚,观察图共有6÷2=3 只兔,所以有8-3=5 只鸡。当然也可以假设全是兔来画图。
有一部分学生会先假设鸡和兔同样多,再调整,如下表:

鸡的只数(只) 兔的只数(只) 总只数(只) 和22 比较4 4 4×2+4×4=24 多2 5 3 5×2+3×4=22 相等
也有思维清晰的学生既不喜欢画图,也不喜欢列表,假设全是鸡,则有脚2×8=16 只,而实际上是22 只脚,少了22-16=6 只,为什么少了6 只脚呢?因为我们把一只兔当作一只鸡来算时,每只少算了2 只脚,所以有6÷2=3 只兔,有鸡8-3=5 只。或者假设全是兔,则脚有4×8=32 只,而实际上是22 只,多了32-22=10 只,为什么多了10 只脚呢?因为我们把一只鸡当作一只兔来算时,每只多算了2只脚,所以有10÷2=5 只鸡,有兔8-5=3 只。
还有少数学生喜欢的是“砍足法”。假如砍去每只鸡、每只兔一半的脚,则鸡就变成了“独脚鸡”,兔就变成了“双脚兔”,则鸡和兔脚的总数就变成了22÷2=11(只),而且有一只兔子,则脚的总数就比头的总数多1,所以脚的总数11 与总头数8 的差,就是兔子的只数,即11-8=3(只),则鸡的只数就是8-3=5(只)。
其实,关于“鸡兔同笼”问题有很多变式题,比如下面两道例题。
例4:全班42 人去公园划船,租10 只船正好坐满。每只大船坐5 人,每只小船坐3 人。租的大船、小船各有多少只?
本题就等同于“鸡兔同笼”问题,本题中的船只数相当于鸡兔总只数,每只大、小船坐的人数分别相当于每只兔、鸡的脚的只数,总人数相当于鸡兔脚的总数。由此分析与联系,便得以轻松解决。不过,有的题目会把一些条件隐藏起来,学生觉得比较难以解决。
例5:一辆汽车在甲、乙两站之间行驶,往返一次共用去4 小时(停车时间不算在内)。汽车去时每小时行45 千米,返回时每小时行30千米,那么甲、乙两站相距多少千米?
这套题目乍一看没法入手,如果教师在教学中先让学生想想题目中的等量关系:往返的路程相等,从而可以根据“去的路程等于回的路程”来思考,而“路程=速度×时间”,发现去、回的速度都已经知道,可是时间只知道“往返一次共用去4 小时”,即“去的用时+回的用时=4 小时”,那么突破点就在时间上了,进而引导学生用假设的策略来解决。
其实,本题也等同于“鸡兔同笼”问题,本题中的“往返总用时”相当于鸡兔总只数,“往、返的速度”分别相当于鸡、兔的脚的只数,经过分析与联系,得出往、返路程相等,由此轻松解决本题。
综合上面例题,先画图假设再调整能更清晰、直观地明白数量关系,先假设再列举也可快速、直接地找到正确答案。也就是说,运用假设策略解决问题时也可借助画图策略或者列举策略帮助理清数量关系,更直观、有效地解决问题。
通过以上例题可以发现,在教学中,教师可以引导学生根据题目的特点建立数量间的联系,运用假设策略,启发学生将难以解决的问题一步步转变为较简便的问题,从而很快地找到解决问题的突破口,进而可以巧妙地解答。这样有利于培养学生思维的逻辑性、准确性和创造性,进一步帮助学生揭示知识的数学本质及其体现的数学思想,理清相关知识间的区别与联系,提高学生学习数学的兴趣。

