(m,n)型二重(r1,r2)左循环矩阵的行列式和逆矩阵

王浩宇, 蔡 静

(湖州师范学院 理学院, 浙江 湖州 313000)

0 引 言

循环矩阵是一类具有优良性质的特殊矩阵，广泛应用于电动力学、图像处理、数理统计等领域[1-2,8-9].关于循环矩阵逆矩阵的计算，始见于文献[2]；1987年邹自兴讨论了对称循环矩阵的求逆问题[3].此后学者们对各种推广形式的循环矩阵进行深入研究，得到了丰富的研究成果[4-6].考虑分块矩阵，若矩阵在每个块里循环，同时块之间也保持循环关系，这样的矩阵被称为分块循环矩阵.分块循环矩阵逆的研究始见于文献[7].由于分块循环矩阵拥有更复杂、更特殊的循环性质，引起了较多学者的关注，提出了K-分块循环矩阵[10]、R-循环分块矩阵[11]等概念，并对这些矩阵逆矩阵的求法、对角化等性质进行了探讨：1983年，De Mazancourt和Gerlic对块循环矩阵的逆进行研究，给出了一种求逆算法[12]；1992年,Zhang等对m阶矩阵因子块循环矩阵的谱分解、反射广义逆、块对角化的计算进行了研究[13]；2001年，Tian探讨了矩阵及块循环矩阵的广义逆[14]；2012年,胡艳等考虑(m,n)型二重(r1,r2)右循环矩阵的逆和广义逆的计算，利用相似变换和矩阵的Kronecker积，给出了求逆算法和逆矩阵[15].

目前被广泛研究的各类循环矩阵的循环方式多为右循环，对左循环矩阵的研究并不多.2014年,Xu等对“RLPrFrL”左循环矩阵进行探究，给出了涉及斐波那契数、卢卡斯数、佩尔数和佩尔-卢卡斯数的“RLPrFrL”等循环矩阵的显式行列式公式[16]；2017年，师白娟研究了广义Fibonacci多项式构成的行斜尾加首左循环矩阵(RSFPLR)的行列式计算方法[17].以上文献尚未对分块左循环矩阵进行研究.本文在文献[15]的基础上，探究(m,n)型二重(r1,r2)左循环矩阵的行列式及其逆矩阵的计算方法,实现该矩阵的合同对角化，并利用合同变换和Vandermonde矩阵得到行列式计算公式和逆矩阵的显式表达式.

1 预备知识

为r2-左循环矩阵.

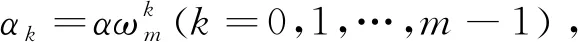
引理2[15]若r2≠0,定义关于βl(l=0,1,…,n-1)的Vandermonde矩阵：

同理，若r1≠0，定义关于αl(l=0,1，…,m-1)的Vandermonde矩阵:

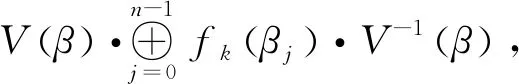
若r2≠0，循环矩阵乘以n阶反单位矩阵Sn可以得到左循环矩阵.因此有:

(1)

其中，

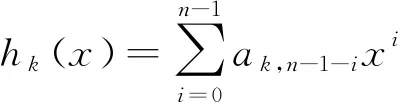
引理4 若r2≠0，则

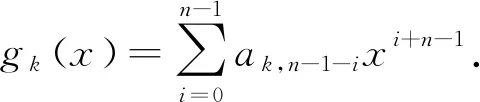
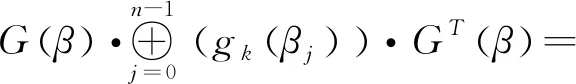
证毕.

定义如下矩阵:

参考式(1)得:

φr1i=V(α)·Ui·V-1(α)·Sm,

(2)

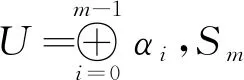
类似引理4，有如下结果：

引理5 若r1≠0，则

2 主要结果

下面给出(m,n)型二重(r1,r2)左循环矩阵的行列式公式和逆矩阵的显式表达式.

定理1 设A为(m,n)型二重(r1,r2)左循环矩阵，若r1≠0，r2≠0，有:

(3)

证明利用定义1中矩阵的表达式及引理4、引理5，可到矩阵A的一种分解形式:

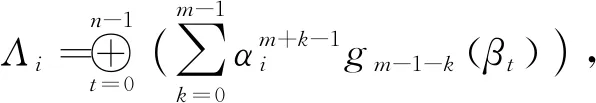
定理2 设A为(m,n)型二重(r1,r2)左循环矩阵，若r1、r2不为0，则有A的另一种分解形式：

(4)

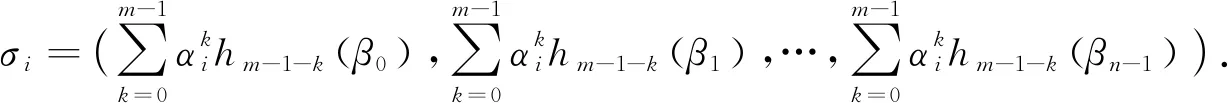
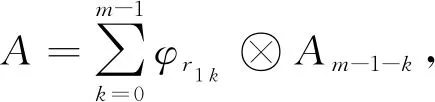
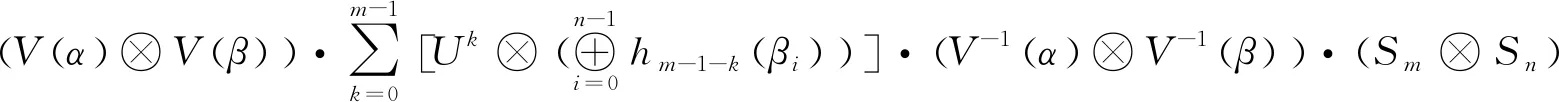
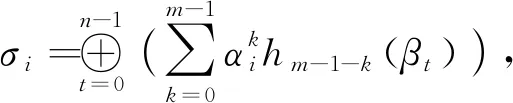
证明由定理2可知：

又由于

定理3 设A为(m,n)型二重(r1,r2)左循环矩阵，若r1≠0，r2≠0，且对于i=0,1,…，m-1；j=0,1,…,n-1,都有gi(βj)≠0，则A的逆可表示为：

证明A为(m,n)型二重(r1,r2)左循环矩阵，若r1≠0，r2≠0，且对于i=0,1,…，m-1；j=0,1,…,n-1,gi(βj)≠0，则Λj的模也不为0，A非退化，故可逆.通过定理1对A的分解可得:

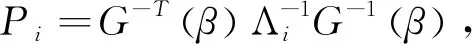
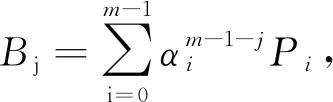
此时Bh可用Dv表示：

3 数值算例

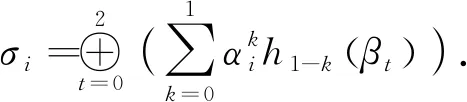
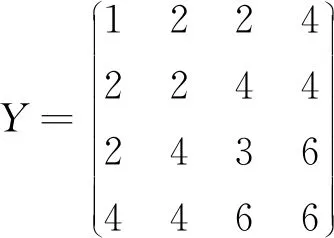
解Y为(2,2)型二重(3,2)左循环矩阵，行列式为4，故可逆，且有:

计算得:D(0,0)=-4，D(0,1)=4，D(1,0)=2，D(1,1)=-2.

因此

从而有:

4 结 论

本文通过合同变换，将(m,n)型二重(r1,r2)左循环矩阵变换为对角矩阵，从而简化了逆的计算难度和复杂程度.本文根据循环矩阵乘以反单位矩阵得到左循环矩阵的结构特点，并将此类分块循环矩阵分解为反单位矩阵、对角矩阵、Vandermonde矩阵等结构较简单的矩阵的乘积，给出该矩阵的行列式计算公式和逆矩阵的计算方法，同时给出数值算例验证了结论的正确性.