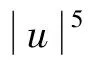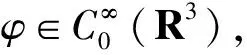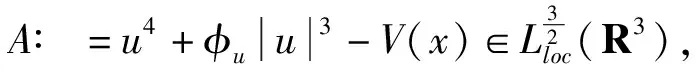带有临界项的薛定谔-泊松系统基态解的存在性
杨 霞,冯晓晶
(山西大学 数学科学学院,山西 太原 030006)
0 引言
本文研究一类带有临界非局部项的薛定谔-泊松系统[1]:
(1)
近几年,越来越多的数学家们研究了下列薛定谔-泊松系统[2]:
(2)

特别地,对带有临界非局部项的薛定谔-泊松系统:
(3)
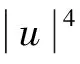
其中:2 系统(1)可以化为Choquard方程: 注:本文中,用C>0表示不同的正常数。 (4) 对任意的u∈Π,有: (5) 引理1[12](Ⅰ)对任意的u∈D,有φu≥0。 (Ⅱ)对任意的t>0和u∈D,有φtu=t5φu。 (Ⅳ)若un在D中弱收敛于u,则存在子列,使得φun在D中弱收敛于φu。 定义能量泛函为: 显然,J∈C1(D,R)。容易证明系统(1)的弱解等价于J的临界点。为了得到基态解(也就是最小能量解),定义Nehari流形N={u∈D{0}:I(u)=0},其中 为了证明主要结果,首先给出一些引理。 引理2假设定理1的条件成立,对任意的w∈Π,存在唯一的tu>0,使得tuu∈N,且有J(tuu)=maxt>0J(tu)。 证明对任意的u∈D,根据Hölder不等式和式(4)得: (6) 取定u∈D{0},对t>0,定义f(t)∶=J(tu),注意到f′(t)=〈J′(tu),u〉=0当且仅当tu∈N,通过计算有: 显然,t>0时,h是不增函数,由式(6)可知: 因此,存在唯一的tu>0,使得f′(tu)=0,即有tuu∈N。从而J(tuu)=maxt>0J(tu)。 引理2证毕。 对任意的u∈N,结合式(4)及式(6),有: 从而不难推得,存在α>0,使得: (7) 根据式(6),对任意的u∈N,有: (8) 知J有下界,则可令m=infu∈NJ(u)且m>0。 引理3假设定理1的条件成立,对任意的u∈N,I′(u)≠0。 证明对任意的u∈N,根据式(6)和式(7),有: (9) 则对任意的u∈N,I′(u)≠0。 引理3证毕。 引理4假设定理1的条件成立,则存在有界序列{un}⊂N,满足J(un)→m,且在D-1中J′(un)→0。 证明利用Ekeland’s变分原理[16],存在有界序列{un}⊂N,{λn}⊂R,使得J(un)→m,并且在D-1中J′(un)-λnI′(un)→0。由式(8)可得: 故{un}在D中有界。又知0=〈J′(un),un〉=λn〈I′(un),un〉+ο(1),结合式(9)可得:λn→0。利用Hölder不等式和{un}的有界性得: 从而有: 引理4证毕。 引理5假设定理1的条件成立,则下面不等式成立: 证明对任意的u∈Π,当t>0时,定义 结合式(5),上式可以化为: 故有: 根据引理2,对任意的w∈Π,存在唯一的tw>0,使得tww∈N,从而有: 因此,m<Λ。 引理5证毕。 引理6假设定理1的条件成立,J有非平凡的临界点。 (10) 利用文献[16]中的引理2.13,有: (11) 再由式(10)及式(11),有: (12) 由引理1,φun在D中弱收敛于φu,则在L6(R3)中有φun弱收敛于φu。从而有: (13) (14) 又显然有: (15) 由式(11)、式(14)、式(15)及J′(un)→0得: 〈J′(u),φ〉=limn→∞〈J′(un),φ〉=0, 由此可得J存在一个非平凡的临界点。 引理6证毕。 定理1的证明由引理6可知:J有一个(PS)m序列{un}⊂N且存在u∈D,使得un在D中弱收敛于u,此外,u∈N有J(u)≥m。通过式(11)及范数的弱下半连续,知: 定理1证毕。



1 预备知识
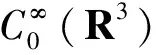
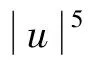

2 定理1的证明