用好数学推理 构建数学模型——人教版四年级下册“四则运算”单元复习的教学实践

□ 陈 芳 李玉兰 孙丹镁

“四则运算”单元的复习，既有对运算概念的回顾，也有运算能力的培养，更有“租船类问题”的解决。因此，这个单元虽然课时不多，却是对整数四则运算意义、四则混合运算与问题解决的总结。在单元复习时，如何在全面复习的基础上，突出重点，构建起意义、运算与问题解决的联系？笔者认为，可以创设数学情境，充分运用数学推理，让学生自己发现和提出问题，进而分析与解决问题。

一、图式推理提升运算能力

本单元练习二的第9 题和第10 题是图式推理题，第9 题是四则运算关系式的灵活推导，第10 题是依据图式中各个式子之间的联系，列出综合算式。我们将这类题型后移到单元复习中，作为复习四则运算意义与四则混合运算的题型。

（一）阅读图式，回顾运算意义

本单元学习的四则运算的定义可以分成两类。第一类是加法与乘法，是从它的本质意义加以概括，加法代表“合并”，乘法代表对“相同加数连加”的优化。第二类是减法与除法，是运算关系的推导。基于这样的理解，可用问题串的形式帮助学生回顾四则运算的意义。

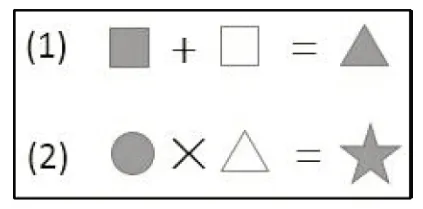
图1

教师出示图1，请学生观察后回答看到了哪两种运算，并说一说这两种运算的含义。学生回答后，教师继续追问：“我们今天要复习‘四则运算’，那么另外两种运算你能够从这两个式子中发现吗？”请学生推导出减法与除法式子，并说一说这两种式子的含义。

从四则运算的逻辑关系来说，加法与乘法是基本运算，减法与除法则是推导得到的运算。通过问题串，学生在不断思考与回忆的过程中复习四则运算的意义结构。

（二）发现联系，列成综合算式

把若干个有联系的一步计算合并成综合算式，是增强学生数学推理能力的载体。笔者在图1 的基础上，呈现图2的两个算式，请学生找一找哪一个算式可以把图1 中的两个算式串联起来。

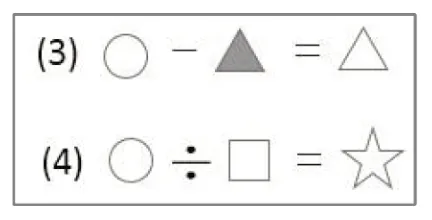
图2

学生独立完成后反馈。生1 展示了连线图（如图3），并说明：“我认为是第3 题。因为第一个算式中的和，是第3 个算式中的减数，第3 个算式中的差又是第2 个算式中的一个因数。”生2展示了图4。

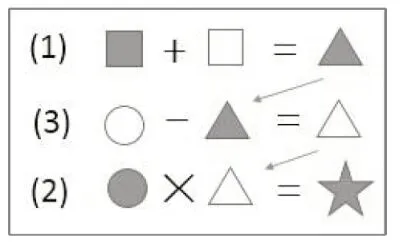
图3

图4

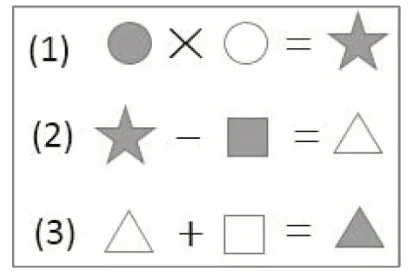
图5

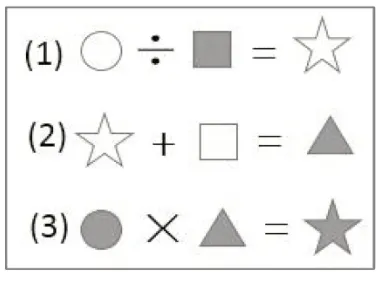
图6

接着教师请学生依据联系把它们写成综合算式，并说一说怎样寻找算式之间的联系。在此基础上再出示如图5 与图6所示的两组图示，请学生寻找关系列成综合算式，最后得到图7的三个综合算式。

图7

（三）赋数运算，熟练四则运算

用图式推导可以让学生更好地探究各个式子之间的联系，以及用运算符号来确定运算顺序与用括号改变运算顺序。在此基础上，引导学生对图7中的三个图式进行观察，可以发现，每个算式中都有四个不同的图形，其中第1 题与第2 题运算符号也相同，只是运算顺序不同。进一步追问：“如果用比1 大的数来代替第1、2 题中的各个图形，哪一题的得数大呢？”

生1：我认为是第1 题大，因为最后一步算乘法，就会越乘越大。

生2：我认为是第2题大，因为第1题的中括号中要减去两个数的和，所以不如第2题中的两个数相乘大。

……

师：大家都有自己的想法，请同学们看这一组数（如图8），把它们代入前两个算式，用递等式计算出结果后进行比较。同时，可以再按要求自己举一组数据代入算式，比较第1、2题的计算结果。

图8

学生计算后发现，不论代入哪一组数据，都是第2个算式的结果大。面对学生产生的疑惑，教师指出到四年级下学期学习了“运算定律”后我们就可以知道为什么会这样了。最后要求学生把图8的这组数据代入第3题中用递等式计算出结果。

总之，从图式推理到四则混合运算，通过不断的观察、操作、比较等活动，学生透过数学事实，构建了数学结构，探究了数学规律。

二、逆向推理灵活运算思维

基于《义务教育数学课程标准（2001 年版）》编写的人教版数学教材，没有四则运算意义与关系的学习内容，这是因为原来学习这种关系是为后续学习解方程服务的，现在解方程是用等式性质了，学习了四则运算的关系式反而会对后面的解方程产生负迁移。如今重新把四则运算的关系作为学习内容，笔者认为，虽然不作为解方程的依据，但是利用关系式，求图形等式中的未知数，可以培养学生的逆向推理能力。

（一）一步推理，回顾关系式

教师出示图9的两个等式，请学生说一说等式中的图形分别表示什么数，可以怎样求。学生独立完成后反馈。

教师引导学生观察求图形代表数的等式（如图10）与原来的等式（如图9）之间的变化规律，引导学生发现减法中是把减数与差交换了位置，除法中是把除数与商交换了位置。教师进一步追问为什么会有这样的规律，引导学生发现原来相应的两个式子还原后是“减数+差=被减数”或“除数×商=被除数”。这样，从减法与除法的角度又一次对四则运算的意义进行了构建。

图9

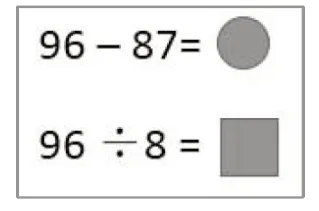
图10

（二）解决问题，感受现实性

如何赋予抽象的计算题以具体的意义？笔者通过提供例子与学生自主编题这两种形式，让学生体会到计算的抽象性与应用问题的现实性。

教师出示如下两组信息：

（1）一个盒子里面装了96颗小球，拿掉了一些后，还剩下87颗。

（2）用96元钱可以买若干支同样的笔，这种笔的单价是8元/支。

在上述信息中，没有单独提出问题，而是把所求问题融入已知信息之中，请学生按顺序阅读并列出数量关系，然后与图9 中的两个等式进行比较，找一找它们之前的对应关系。接着请学生读题找一找，信息中哪一些词代表了图形的含义，哪一些词代表了运算符号的含义，哪一些词又代表了相等关系。

在文字叙述信息中寻找确定数量关系的词，可以体会到抽象的数学符号的实际意义。在寻找“等号”所代表的词时，学生出现了困惑，如第1题按叙述的顺序应该是“还剩下”，但学生认为这里只是指剩下的“87 颗”。这时，教师引导学生往回看，提问：“‘总颗数-拿掉的颗数’是什么意思？”学生发现也是指“剩下的颗数”。所以等号左边表示的是剩下的颗数，右边也表示剩下的颗数，只是左边是算式，右边是数据，在算术意义的数量关系中渗透代数意义的相等关系。

在此基础上，请学生模仿上面的编题方法，自己依据图9中的图式来编制应用问题，并在四人小组中交流。

（三）两步推理，体会有序性

与图9相比，图11中的两题等号左边出现了两步运算，这时该怎样推算图形所代表的数呢？需要用到转化，即转化成可以直接应用四则运算关系式进行推算的题目。

图11

师：请说一说图11中的题目与图9中的有什么不一样的地方。

生1：（图9）原来两题等号左边是一步，（图11）新的两题等号左边变成两步了。

师：如果要求出图形表示的数，需要怎样做？

生2：第（1）题很简单，只要算出“14+82”的和就变成一步了。但第（2）题我不知道如何做，因为“96÷”算不出得数。

师：大家能够听懂这两位同学的思路吗？请同学们依据他们提供的思路，把两个题目转化成求图形结果的算式，然后计算出结果。

学生完成后反馈，教师再提出要求：怎样检验结果是否正确？

上面的两道题，分别对应五年级上学期简单的与较复杂的解方程，但教学目标不同，在这里不仅仅是为了求出未知数，而是为了培养学生利用四则运算关系式进行逆向推理的能力。

三、合情推理培养应用意识

本单元的“租船类问题”要求基于运算进行合情推理，随着数据的不断变化，“最省钱”的方案会发生变化，这就需要依据一定的思路，罗列出可能“最省钱”的各种方案，并计算结果进行比较，这种思路也可以迁移到用假设法解决问题，形成更加一般的解决问题的思维模型。

（一）夯实基础，回顾基本思路

单元复习习题的设计要做到低起点、有变式与可持续。低起点即习题设计要涉及本单元中最基本的数学知识与思维方式，“租船类问题”最基本的思路就是如例题5的形式，经过一次调整后就可以不出现空位。

教师出示如下题目：有20个同学去划船，每条大船可以坐6 人，租金是90 元；每条小船可以坐4人，租金是80元。怎样租船最合算？

依据解题过程，回顾租船问题的一般思路，为后续的变式练习与思维迁移夯实基础。

（二）变式练习，发现内在规律

在新课教学中，“租船类问题”已经有了多种变式，教师要让学生感受到经历完整思考过程的重要性。在之前的各种方案中，经调整后均不会出现空位。但是，会不会出现调整后还是有空位的情况呢？答案是肯定的。

教师把上面租船问题中的“20 个同学”改为“21 个同学”，让学生用原有思路解决问题。学生发现，调整后还是有空位（如图12）。

图12

教师请学生进一步观察列出的数据，思考为什么比原来增加了一个人，就不可能没有空位了。依据班级的基础与时间，可以只提出问题，不展开讨论。

（三）拓展练习，应用学习策略

把某一类型解决问题思路一般化，为后续的学习提供思维模型，是“租船类问题”思维拓展的方向。

教师对上述的租船问题进行了改编：有20 个同学一共租了4 条船去划船，其中每条大船坐满6人，每条小船坐满4人。大船和小船各租了多少条？

如果分析题型结构，这是本册教材后面要学习的“鸡兔同笼”问题。但它同样可以用“租船类问题”来思考。

20人假设全部租大船，那么20÷6=3（条）……2（人），使其中一条大船上的人和余下的2人合并租小船，那么小船租了（6+2）÷4=2（条），已知大船与小船一共租了4条。所以大船和小船各租了2条。

从上述思考过程中可以发现假设法的痕迹。因此，“租船类问题”“鸡兔同笼问题”的分析思路，实际上都可以看成合情推理，即先假设某一种方案，如果不正确就进行调整，逐步得到最终的结果。

总之，本单元的课题虽然叫作“四则运算”，但是“四则运算”只是其中最基础的部分，在概括出四种运算意义与关系的基础上，结合具体例子与解决实际问题，让学生运用数学推理，逐步构建基于运算与问题解决的数学思维模型。