基于粒子群的非规则区域连续覆盖星座设计

刘 明 杨 明 高 兴 杨 丁 葛亚杰

1.国防科技大学, 长沙410073 2.空间物理重点实验室, 北京100076

0 引言

采用对地静止轨道卫星进行网络通信传输服务具有发射成本高、空间资源有限等缺点，近年来，随着各类微小卫星和低成本、快速响应运载器技术的发展，利用近地轨道卫星组网来执行网络通信传输服务已成为各国的研究热点。美国Space-x公司提出的“星链计划”以及中国的“虹云工程”即属于此类低轨星座，且都已成功部署相关技术验证卫星。近地轨道卫星组网实现区域覆盖时，要求单颗卫星的星下点能够实现周期性的重复，从而保证在某天的固定时段或者全天候对特定区域进行连续覆盖，圆回归轨道的轨道高度均匀，适合进行对地观测，此类星座中的单颗卫星轨道通常基于圆回归轨道进行设计[1]。共地面轨迹星座是一类特殊的星座形式，星座中的所有卫星具有一致的星下点运行轨迹，适用于特定区域的覆盖系统[2]。近地轨道卫星区域周期性连续覆盖星座的设计方法主要分为解析法和优化法。朱仁璋讨论了卫星循环轨道问题并给出了一种覆盖轨道的设计方法[3]，吴廷勇等针对高轨通信卫星对规则区域连续覆盖问题，采用遗传算法求解了共星下点轨迹星座的设计问题[2,4-5]。Gao等考虑传感器模型，针对特定纬度范围内具有一定时间间隔的覆盖问题，采用解析法设计了星座参数[6]。文献[7-8]将包含特定目标城市的规则区域连续覆盖星座设计问题转化为多目标优化问题进行了求解。张文敦基于解析法设计了针对特定目标点覆盖任务的共星下点轨迹星座，并采用遗传算法对星座组网形式进行了优化[9]。马剑等考虑重访周期约束，以星座内卫星数量最少为目标，优化设计了共星下点轨迹星座实现了对规则区域的覆盖[10]。范丽提出一种搭载不同有效载荷的区域覆盖混合星座设计方法[11]。

针对非规则区域连续覆盖星座设计问题，受推导条件限制，以上研究成果的解析法难以直接解析求解星座设计参数[12]；而采用数值寻优的方式，较多优化变量的星座设计参数将会导致计算效率较差[13-15]。针对该问题，本文采用了一种具有回归轨道属性的共星下点轨迹星座方案，提出了一种优化法与解析法相结合的星座优化设计方法，基于卫星对地观测的传感器视场覆盖模型，采用粒子群算法(PSO)优化算法，以非规则区域覆盖范围最大为性能指标，选择轨道倾角和升交点赤经为优化变量，获得单颗卫星的最优轨道参数，在此基础上，根据共星下点轨迹星座约束关系，解析求解星座轨道参数，可实现星座轨道的快速求解，同时满足非规则区域连续覆盖的性能要求。

1 回归轨道计算模型

针对圆轨道卫星，建立地心惯性坐标系E-xyz，原点位于地心，其中x轴在赤道平面内指向春分点方向，z轴由地心指向北极，y轴构成右手坐标系。如图1所示的轨道半径a、轨道倾角i、升交点赤经Ω、纬度幅角u(升交点到卫星所在位置的地心夹角)4个参数即可表示卫星在空间中的位置。

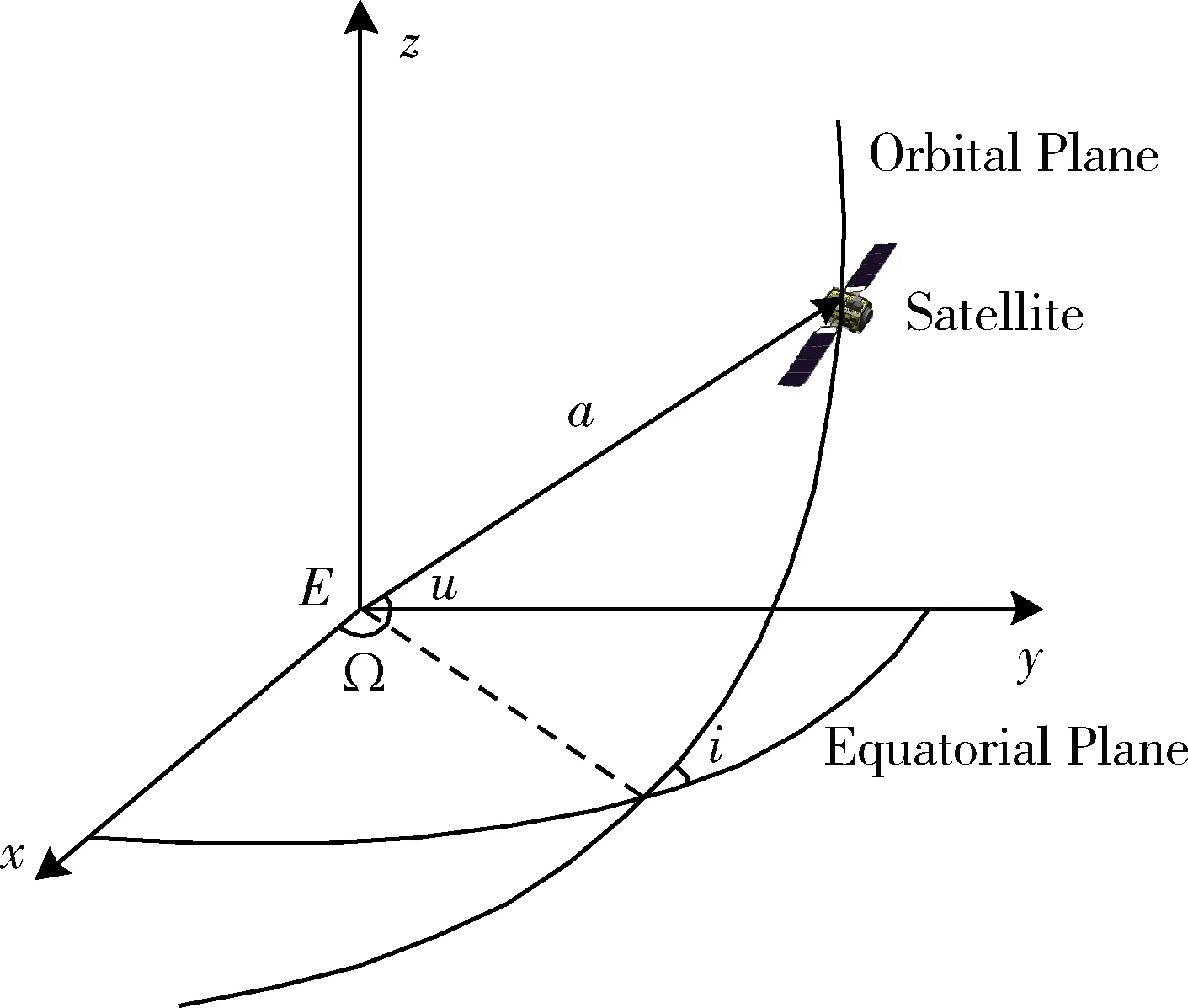
图1 圆轨道描述参数示意图

地球引力非球形摄动(地球并不是一个正球体，其内部的密度分布不均匀而产生的摄动称为非球形摄动)对近地轨道具有较大的影响，卫星升交点赤经Ω与纬度幅角u随在轨时间的变化而变化，其变化趋势由轨道半径a和轨道倾角i确定。J2项是非球形摄动的主要摄动项，考虑J2项摄动可满足近地轨道设计时的精度要求，相应升交点赤经与纬度幅角平均摄动为

(1)

(2)

其中，RE为轨道半径，ω为圆轨道角速度。

轨道周期T定义为卫星由升交点出发绕行一周再次回到升交点的时长，可根据下式进行计算

(3)

因此，一个轨道周期内升交点赤经的增量ΔΩ为

(4)

式中，ωe为地球自转角速度。

回归轨道或准回归轨道是星下点按照一定周期重复的轨道，回归轨道卫星的星下点轨迹重复周期为1天，准回归轨道的重复周期为多天。当满足式(5)时，星下点轨迹在d天后恰好转过n圈回到原位。

n·ΔΩ=2π·d

(5)

当d为1时，式(5)表示回归轨道条件，当d大于1时，表示准回归轨道条件。以下讨论的所有问题均为回归轨道问题，因此，式(5)可以改写为

n·ΔΩ=2π

(6)

即卫星在一天时间内运行n圈后，星下点轨迹回归，联立式(3)和式(4)得到

(7)

将式(1)与式(2)代入式(7)，得到考虑J2项摄动的回归轨道条件

(8)

通常而言，轨道高度H小于500km时，气动力摄动项对轨道的影响较大，将引起卫星能量的耗散，轨道高度难以长时间保持，因此近地轨道高度H一般在500km至1000km之间。由于J2项摄动在式(8)中的影响较小，可忽略其影响，估算H∈[500km,1000km]时，所对应的回归周期T内的运行圈数n∈[13.66,15.18]，取整后n=14，15，其相应的轨道高度约为800km以及500km。

2 共星下点轨迹星座约束条件

近地回归轨道卫星只能以回归周期一天为时间间隔对覆盖区域进行重访，无法在较长时间内实现持续性的覆盖。针对此类任务，具有回归轨道属性的共星下点轨迹星座可实现对特定区域的周期性连续覆盖。此卫星组网星座的优点是满足单颗卫星的覆盖效果最优时，组网形成的星座覆盖效果最好。共星下点轨迹星座设计一系列轨道高度与轨道倾角相同的近地回归轨道，每个轨道面内一颗卫星，考虑地球自转特性、回归轨道参数、传感器模型的条件下，通过设计各轨道面间的升交点经度差ΔΩ以及纬度幅角差Δu，实现对特定区域的周期性连续覆盖。

如图2所示为相邻轨道面内两颗卫星的空间几何关系，卫星Si的升交点赤经为Ωi，卫星Sj的升交点赤经为Ωj，两轨道面的升交点赤经差值ΔΩ=|Ωi-Ωj|，两轨道同为顺行轨道，Δu是卫星Sj滞后于卫星Si的纬度幅角差值。

图2 相邻轨道面卫星空间几何关系

由图2可知，若卫星Sj由当前位置运行到其升交点λj的时间和地球自转ΔΩ的时间相同，则卫星Si和Sj具有相同的星下点轨迹，由此可得共星下点轨迹星座相邻轨道面卫星应满足的条件为

(9)

考虑地球非球形引力摄动J2项，将式(1)和式(2)代入式(9)得到

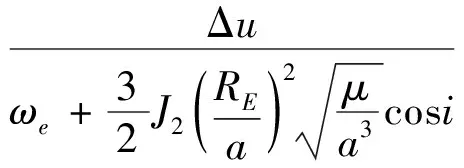
(10)

依据式(10)即可在已知相邻轨道纬度幅角相位差Δu的条件下，快速解析计算升交点赤经差值ΔΩ。

3 非规则区域连续覆盖星座设计方法

3.1 基于传感器特性的星座分布设计

卫星通常携带各类传感器作为有效载荷，实现对地面目标的通信中继、对地观测等任务，其覆盖范围通常由轨道高度、传感器视场角、传感器视场形状等因素决定，典型的对地观测为圆锥形视场传感器，圆锥形传感器的视场如图3所示，卫星所在位置为S，星下点为S′，其轨道高度为SS′长度H，视场半锥角(Cone Half Angle)定义为θ，每一时刻传感器所覆盖的圆形区域半径AS′长度为d，扫过的地面幅宽为2d，视场投影半径d可根据集合关系计算

d=H·tan(θ)

(11)

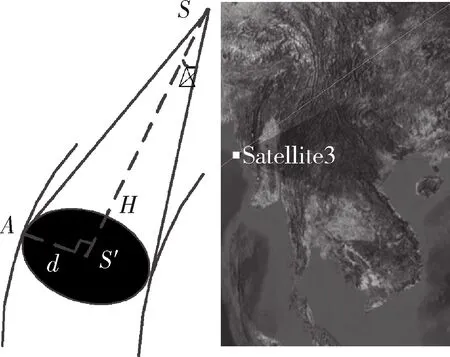
图3 圆锥形传感器示意图

(12)

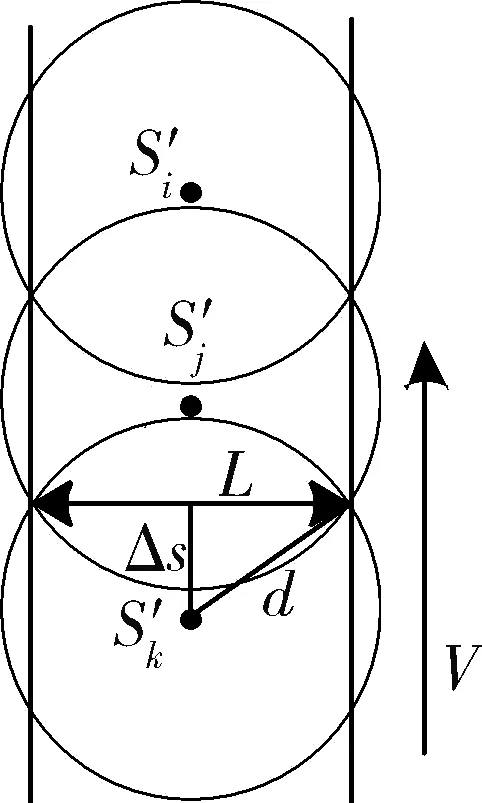
图4 圆锥形传感器地面覆盖区域示意图

在确定两星下点轨迹距离2Δs的条件下，可求出相应的地心夹角β

β=2Δs/R

(13)

其中，R为地球平均半径。地心夹角β即为相邻轨道面纬度幅角差Δu。

一条完整的共地面轨迹卫星环所分布的卫星数量由式(14)计算

m=2π/β

(14)

若m不为整数，应对其向上取整。

3.2 单颗卫星轨道参数优化数学模型

由于星座内卫星星下点轨迹相同，只要单颗卫星的覆盖效果最佳，即可保证星座对于特定区域的覆盖效果最佳。分析可知，共星下点轨迹星座的设计参数主要包含：轨道半径a；轨道倾角i；卫星总数；星座内第1颗卫星的升交点赤经Ωo；相邻轨道面间的升交点赤经差ΔΩ。

已知传感器特性，对覆盖效果产生影响的参数主要包括a、i和Ωo。定义传感器1个轨道周期内所扫过的面积在总面积中的占比为特定区域周期累计覆盖率η。在轨道半径以及传感器视场角选定的情况下，累计覆盖率仅与i及Ωo相关，因此在合理选取轨道半径以及传感器视场角的情况下，只需对i和Ωo进行优化设计。建立如下的优化问题数学模型，性能指标为特定区域周期累计覆盖率η最大。

(15)

其中，[imin,imax]为优化i的取值范围，[Ωmin,Ωmax]为优化Ωo的取值范围。以上优化变量的约束根据任务区域的形状及位置确定。

3.3 基于粒子群算法(PSO)求解优化问题

选用粒子群算法(PSO)求解式(15)所示的参数优化问题，PSO算法起源于对鸟群捕食行为的观察和研究，其基本设计思想来源于2个方面：人工生命和进化计算。在PSO算法中，用没有质量和体积的粒子来模拟捕食的鸟，每个粒子只有简单的行为规则，通过粒子间的集体协作使群体达到最优[15]。

PSO算法中，每个粒子根据它自身和群体的经验，向更好的位置“飞行”。粒子本身找到的最优解称为个体最优位置，就是每个粒子在飞行过程所经历过的最好位置。整个群体目前找到的最优解称为全局最优值，就是整个群体所经历过的最好位置。分别用D维速度矢量Vq=(v1,v2,…,vqd,…,vqD)和位置矢量Xq=(x1,x2,…,xqd,…,xqD)表示第q个粒子的状态，则每个粒子根据以下公式来更新自己的速度和位置，从而产生新一代群体。

(16)

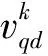
PSO算法的主要运算过程如下：

1)初始化。在问题搜索空间允许范围内随机设置粒子的初始位置和速度，设定PSO算法参数和算法终止条件。

2)适应度评价。根据目标函数计算每个粒子的合适值，根据个体极值和全局极值评选条件，计算每个粒子的最优和群体的最优。

3)更新粒子。根据粒子速度和位置更新公式计算，并根据粒子速度和位置的限定范围，调整粒子位置和速度。

4)算法结束判断。检查终止条件，如果满足条件则终止算法，输出最优解，否则转到步骤2，继续迭代。

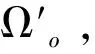
(17)

3.4 非规则区域连续覆盖星座设计流程

采用回归轨道的共地面轨迹星座优化设计流程为：

1)依据覆盖区域的位置形状，确定轨道倾角i以及首颗卫星的升交点赤经Ωo取值范围，基于3.3节所述的参数优化方法求取一个轨道周期内累计覆盖率最大所对应的轨道倾角i以及Ωo；

2)已知轨道倾角i，选取回归周期内运行圈数n，迭代求解式(8)等于0时所对应的轨道半径a，进而求得轨道高度H；

3)已知轨道高度H，依据传感器类型以及覆盖区域幅宽约束，设计合理的传感器视场角，基于3.1节方法计算共地面轨迹卫星环内所包含的卫星总数m及纬度幅角差值Δu；

4)根据持续覆盖时间长度，计算共地面轨迹卫星环数量C，从而得到卫星总数N；

5)基于式(10)计算得到各卫星升交点赤经Ωq(q=1,…,N)以及纬度幅角uq(q=1,…,N)，完成共地面轨迹星座设计。

图5 星座设计流程

4 仿真验证

仿真中的覆盖区域为以Place1(18.45°N,108.97°E)，Place2(36.71°N ,126.46°E)，Place3(40.24°N ,115.46°E)，Place4(22.23°N ,97.36°E)四地位置坐标连线构成的非规则封闭区域，覆盖时间为每天的00：00(UTCG)至03：00(UTCG)的不间断覆盖，卫星传感器类型为圆锥形传感器，视场半锥角为50°。

按照3.4节所述的设计步骤，对首颗卫星的升交点赤经Ωo以及轨道倾角i进行优化设计，相应的取值范围为Ωo∈[105,150]，i∈[30,70]。在卫星轨道高度为800km，选择传感器视场半锥角(Cone Half Angle)θ为50°的条件下，一个周期的累计覆盖率η随Ωo及i变化的趋势如图6所示。

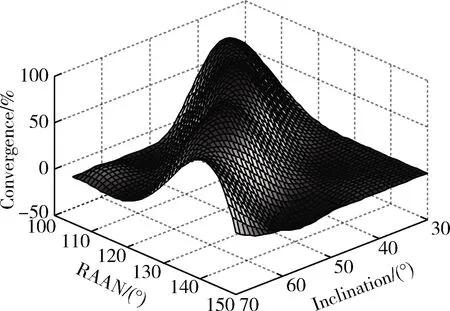
图6 单周期累计覆盖率随升交点赤经及轨道倾角变化趋势

采用粒子群算法(PSO)优化得到首颗卫星升交点赤经Ωo为127.5°，轨道倾角i为55°。选取回归周期内运行圈数n为14。采用迭代方法求解等式约束式(8)，获得对应的轨道半径a为7211.14km，相应的轨道高度H为833km。

传感器视场半锥角(Cone Half Angle)θ为50°的条件下，基于3.1节方法计算共地面轨迹星座内相邻卫星的纬度幅角差值Δu应为18°，相邻卫星的升交点赤经差值ΔΩ为1.286°。

相邻卫星空间相对位置及覆盖特性如图7所示，一条完整的共地面轨迹卫星环所需卫星数量m为20颗，为实现3小时连续覆盖，共地面轨迹卫星环数量C=1.5，从而得到卫星总数N=30，基于STK的仿真表明，所设计的共地面轨迹星座可以实现所要求的非规则区域每日固定时间连续覆盖3小时的需求。

图7 相邻卫星空间位置及覆盖特性

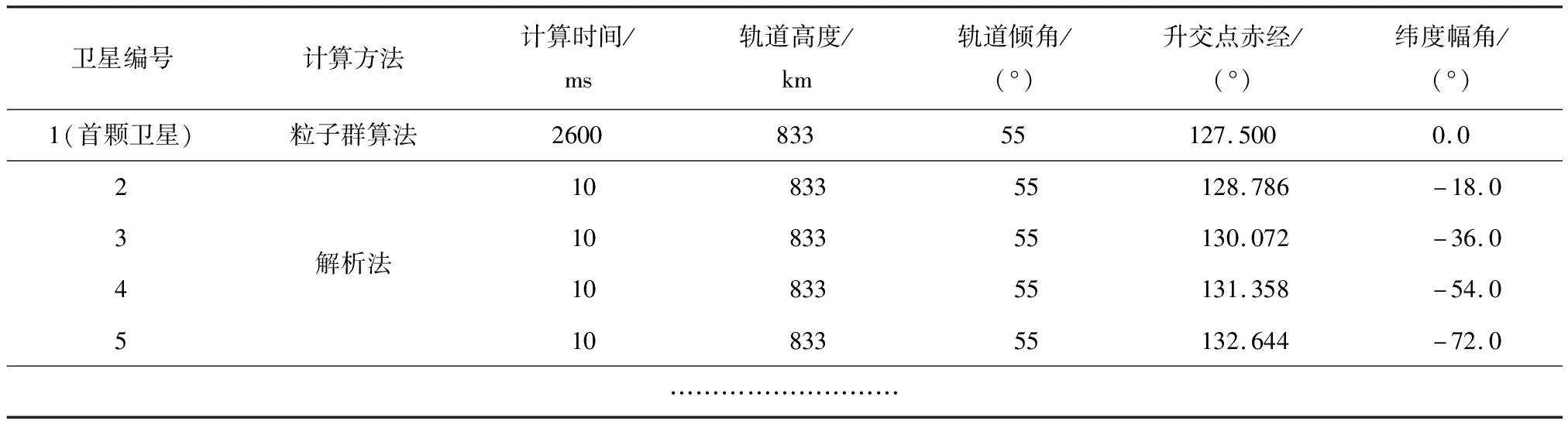
表1 星座组网参数

上述对非规则区域3小时的连续覆盖仿真的问题中，30颗卫星可实现100%非规则区域的连续覆盖要求，对应星座轨道参数的计算时间在5s以内，表明该方法求解效率高，星座覆盖效果好。

5 结论

针对非规则区域连续覆盖的问题，采用回归轨道的共星下点轨迹星座方案，设计了一种优化法与解析法相结合的星座优化设计方法。该方法基于粒子群算法(PSO)优化求解单颗卫星轨道参数，共星下点轨迹星座约束关系解析求解星座轨道参数，具有较高的求解效率，为卫星组网的工程实现提供了新的设计思路和新途径。