税收竞争对中国制造业全要素生产率的影响——基于总量与结构双重视角的实证分析

（华中科技大学经济学院，武汉 430074）

引 言

自1978年改革开放以来，我国经济维持40年的高速增长，GDP占世界比例由1978年的1.8%提高到2016年的近15%，上升成为世界第二大经济体。但是至2015年以来，我国经济增速放缓，经济发展进入新常态，现正处于转变发展方式、优化经济结构、转换增长动力的攻关期。制造业是国民经济的支柱产业，也是我国经济增长的主导部门，其发展对我国经济结构转型具有基础性作用。税收是财政政策的重要工具，当前经济下行压力大，如何有效运用税收手段对国家宏观经济进行调控、发挥制造业对产业的拉动效应，推动我国经济向高质量升级成为我们亟待解决的问题。全要素生产率作为反映经济高质量发展水平的指标之一，能够定量研究税收竞争对制造业全要素生产率的影响，从税收角度提出实现制造业高质量发展的举措，对于实现我国经济增长方式转变十分关键。

目前很多学者研究税收竞争对生产率的影响，研究观点主要有3种：

（1）税收竞争促进了生产率。郑宝红和张兆国 （2018）认为税收竞争通过优化要素市场资源配置、缓解企业融资约束、促进企业研发投入和人力资本投入促进了企业全要素生产率［1］。于文超等 （2015）认为减少企业的税负有利于增加税后利润，扩大生产性领域的投资，从而提高企业生产率［2］。刘伟江和吕镯 （2017） 通过构造空间SLX模型，实证发现本地区的税收激励、其他地区的税收竞争以及二者的总效应，均能促进本地区高技术产业全要素生产率［3］。

（2）税收竞争抑制了生产率。唐飞鹏等认为辖区间为了吸引企业入驻，竞相采取的税收优惠政策可能削弱财政收入，降低地方政府提供公共品的能力，导致公共品外部性减少进而抑制生产率［4，5］。 Rodrik （2004） 认为企业会为了获得税收优惠而寻租，而不是将资源用于全要素生产率的提高［6］。 彭馨 （2018） 利用1998～2006年的中国工业企业数据，实证发现营业税的整体和省内竞争不利于企业生产率［7］。

（3）税收竞争对生产率的影响并非线性。朱玉飞和安磊 （2018）通过实证发现企业税收负担与企业全要素生产率呈倒U型关系［8］。杨莎莉等（2019）认为，一定程度的税收优惠能够促进企业全要素生产率，但是当税收优惠超过一定程度后，会降低企业研发投入的积极性，不利于企业全要素生产率的提升［9］。许依敏 （2018） 以2008～2015年部分制造业上市公司为对象，构建门槛效应模型进行实证检验，得出企业所得税、流转税均存在对全要素生产率由促进转为抑制的门槛值［10］。

以往研究主要从微观企业层面研究了税收优惠、税率以及税收激励等对企业生产效率的影响，本文在已有研究的基础上试图在以下方面做出创新： （1）在研究视角方面，本文主要聚焦制造业，从税收总量和结构上，研究总税收、所得税、增值税竞争对制造业全要素生产率的影响，丰富了研究视角； （2）本文通过构建门槛效应模型，进一步探讨总税收、所得税和增值税竞争对制造业全要素生产率的非线性关系。

1 理论分析与假说提出

征税会扭曲资源的配置，无序的税收竞争会严重偏离税收中性的原则，增加税收竞争的成本，带来经济的不效率［11］。对微观企业来说，税收优惠会降低企业的生产成本，提高企业的产品收益率，影响企业的投资结构。近几十年来，在唯GDP的考核机制下，地方政府为了提升当地的经济增长速度，竞相利用税收优惠、财政返还、削减地价的方式给予部分行业优惠，鼓励企业扩大投资，甚至造成了非理性的投资，导致我国产业的同构化与产能过剩。此外，部分学者认为，辖区间以降低税负的形式招商引资，会降低财政收入，公共品的提供相应减少。这不仅会降低已有企业的生产率，而且还会反过来影响资本与劳动的流入，不利于当地制造业全要素生产率的提升［4，5］。

在税制结构方面，企业所得税是地方政府税收竞争的重要形式。增值税是我国第一大税种，主要在生产环节征税，它与所得税一起构成了制造业企业最重要的税负。因此，地方政府针对制造业企业展开的税收竞争，主要是围绕所得税与增值税的竞争。在征收对象上，所得税涉及的是所有行业的企业，增值税则针对工业企业［12］，制造业作为工业的主要组成部分，是增值税贡献的主体。制造业相比其他行业具有研发周期长、见效慢的特点，因此所得税优惠可能引起资本流向投资回报快的行业，从而减少流入制造业的资本要素，不利于制造业企业技术创新和扩大规模。与所得税优惠不同，地方政府在增值税上的优惠会使得更多的要素资源流入制造业，有利于制造业企业研发创新、扩大规模，形成集聚经济。创新是制造业的灵魂，提高研发投入，是提升制造业生产效率的根本举措。而且制造业的集聚会通过知识、技术外溢效应带来额外的技术进步，进一步提升企业生产率［13］。在优惠方式上，增值税是直接进行税收减免，所得税则是通过先征后返或者补贴的方式［14］，这使企业在最需要研发资金的时候，由于征税反而加重企业的纳税负担［15］。在征税方式上，增值税是对增加值部分征税，而且可以进项税额抵扣，不存在重复征税，因此有促进行业分工专业化的功能［16］，有利于提高各个环节的生产效率。

基于以上分析，提出以下假说：

假说1：地方政府在总量上的税收竞争不利于提高制造业全要素生产率。在税制结构上，地方政府在所得税上的税收竞争不利于提高制造业全要素生产率，在增值税上的税收竞争有利于提高制造业全要素生产率。

在经济较发达的地区，地方政府财政充裕，地方政府可以将更多的资金投资于公共基础设施、教育等方面，改善企业生产经营的外部环境，容易吸引企业到当地投资 （Combes等， 2010）［17］，从而扩大规模形成制造业集聚，获得规模效应与溢出效应。同时，经济发达地区通常具有发达的金融服务业，这缓解了制造业企业面临的融资约束，加之经济发达地区的市场竞争更激烈，企业更有能力也更有意愿进行研发创新。上述因素在一定程度上抵消了税收竞争对资源配置的扭曲作用，缓解了税收竞争对制造业全要素生产率的抑制程度。

在税制结构方面，如上文分析，所得税竞争会使流入制造业的资本要素减少，但是发达经济地区的公共品供给充分，基础设施完善，而且拥有良好的营商环境，对要素资本有足够的吸引力，因此前述情况不复存在。此外，在经济发达地区金融服务业发展较好，企业可从金融机构提前获得资金，改善由于先征后返的优惠方式带来资金的时滞问题。因此所得税优惠可能会促进制造业企业进行研发项目的投资和扩大规模，提升生产效率。

增值税不仅涉及征缴环节，还涉及抵扣环节。相对经济不发达地区，发达地区企业的生产经营业务丰富，产业链完善，增值税征缴抵扣规范健全，更有利于发挥增值税的专业分工作用，提高生产效率。同时在经济发达地区，同行业企业数量众多，制造业作为高度依赖技术进步的行业，发达地区更愿意将增值税优惠的结余资金用于研发投入，以保持在竞争中的优势地位，提升生产效率。

基于以上分析，提出以下假说：

假说2：在经济较为发达的地区，地方政府在税收总量上的竞争使制造业全要素生产率的抑制作用得到缓解。

假说3：经济发展到一定程度后，所得税竞争对制造业全要素生产率的作用将由抑制转变为促进。而经济越发达的地区，增值税竞争对制造业全要素生产率的促进作用越强。

2 实证设计

2.1 计量模型设定

为了分析税收竞争对制造业全要素生产率的影响，本文首先建立模型 （1）以检验研究假说。

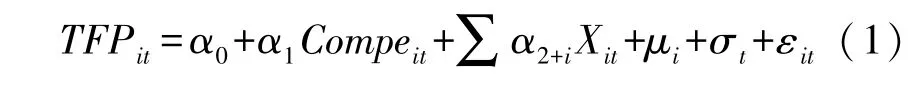
其中，下标i和t分别代表第i省第t年，TFPit代表制造业全要素生产率，Compeit代表税收竞争。Xit代表可能影响制造业全要素生产率的一系列控制变量，具体包括：外商直接投资、研发投入、人均国内生产总值、人力资本。μi和σt代表个体和时间固定效应，εit为随机干扰项。

2.2 变量及数据说明

（1）被解释变量：制造业全要素生产率。借鉴已有学者的做法，本文采用DEA的Malmquist指数方法来测算制造业全要素增长率，该方法的原理是利用两个时期距离函数的比例来计算投入产出效率。可将全要素增长率 （TFP）分解为技术效率指数 （EFFCH）与技术进步指数 （TECH）两个部分。基于数据的可获得性，本文选取制造业中21个行业作为分析对象，选取这些行业工业销售总产值作为产出指标，固定资产净值和从业人员年平均数作为投入指标。该方法测算得到的生产率是相对上一年的变化率，参考部分学者的做法，将其换算为绝对全要素生产率。

（2）核心解释变量：税收竞争指标借鉴付勇和张宴 （2015）［18］的做法， 采用式 （2） 计算。

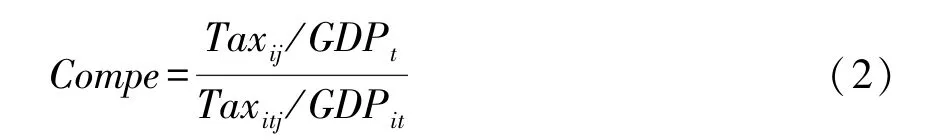
在式 （2）中，Tax表示税收收入总和，GDP表示生产总值总和，t代表年份，i代表省份，j＝1，2，3，分别代表总税收、企业所得税和增值税。Taxij／GDPt表示t年j项税收所有样本地区的平均税负率，Taxitj／GDPit表示第i个省份t年的第j项税收的平均税负率。该指标越大，税收竞争程度越高。

（3）控制变量：①外商直接投资，以外商直接投资额占生产总值之比表示，由于 《中国统计年鉴》中外商直接投资以美元为单位，本文采用各个年度的人民币平均汇率进行换算；②研发投入，以研究与试验发展经费内部支出与生产总值的比值表示；③人均生产总值，以万元为单位；④人力资本，采用就业人员中大专及以上人口比重乘以100并取其对数。

（4）数据说明。样本由2007～2018年30个省级层面的面板数据组成，考虑到西藏和港、澳、台地区数据缺失严重，故在样本中将以上地区剔除。各变量原始数据来源：《中国统计年鉴》、《中国工业统计年鉴》、Wind数据库。具体变量描述性统计见表1。

3 实证结果分析

本文对模型 （1）进行豪斯曼检验，检验结果显示6个模型适用于固定效应模型，3个模型适合用随机效应模型。

3.1 基准回归结果

列 （2）～（4）分别检验了总税收竞争、所得税竞争与增值税竞争对制造业全要素生产率的影响，其中总税收竞争、所得税竞争的估计系数在1%的显著性水平下为负，说明总税收竞争、所得税竞争不利于制造业全要素生产率的提升。增值税竞争系数在5%的显著性水平下为正，说明增值税竞争促进了制造业全要素生产率的提升。回归结果支持假说1。

控制变量中，研发投入系数在1%的显著性水平上为负，说明我国的研发经费投入并没有促进制造业全要素生产率的提升，得到类似结论的有傅元海等 （2016）［19］。人均GDP的估计系数在1%的显著性水平上显著为正，说明人均报酬越高的地区，工人劳动积极性越高，同时收入的增加使工人可以学习新技术，进一步促进了制造业全要素生产率的提升。

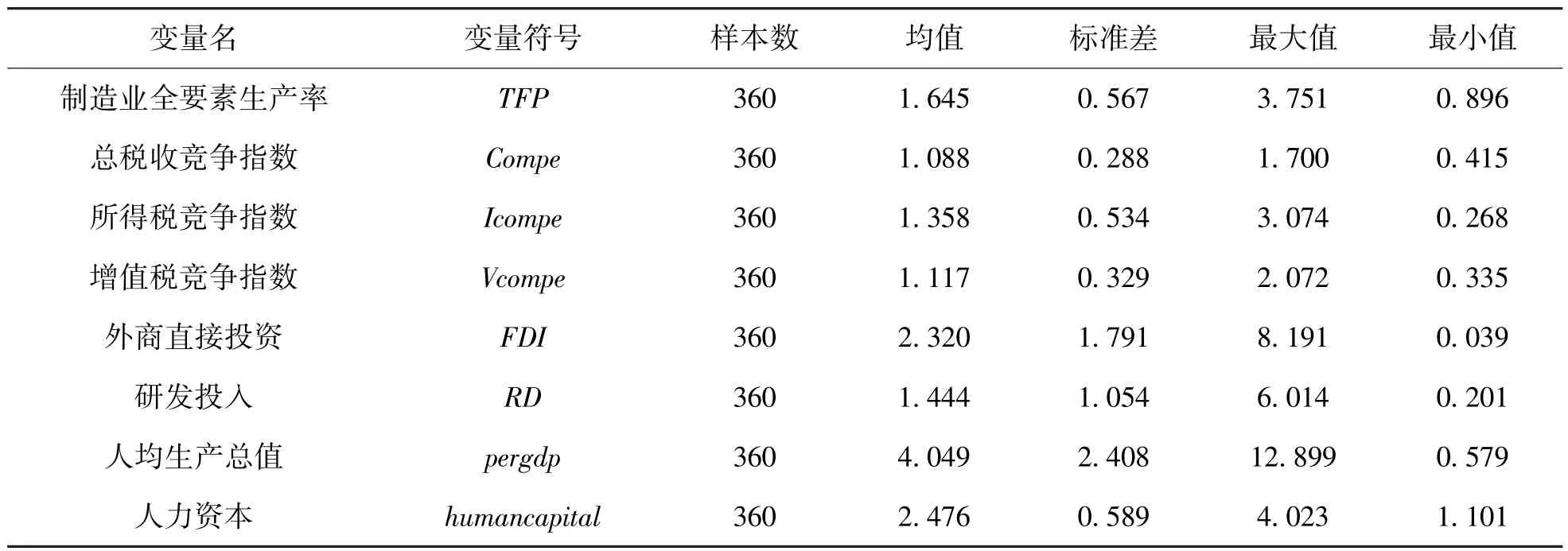
表1 变量的描述性统计

表2 基准回归结果

3.2 内生性处理

理论上，税收竞争与制造业全要素生产率之间存在双向因果关系。税收优惠的增加，通过改变公共产品的供给水平以及影响企业的投资决策，影响制造业全要素生产率；制造业企业生产效率的提高也会增加当地税收收入，进而影响税收竞争程度，因此模型可能存在内生性。本文选择总税收竞争、所得税竞争、增值税竞争的一阶滞后项作为相应内生变量的工具变量，进行两阶段最小二乘估计，回归结果表略。可以看出，在考虑内生性后，总税收竞争、所得税竞争系数在1%的显著性水平上为负，增值税竞争系数在5%的显著性水平上为正，与基准回归结果一致，不存在谬误回归。

3.3 稳健性检验

本文分别通过替换指标与抽取子样本的方法进行稳健性检验，借鉴唐飞鹏 （2017）［5］的方法，通过等式构建税收竞争指标进行稳健性检验，交互项代表本地区与其他地区的税收竞争策略互动的结果。Wi，j代表经济地理矩阵，主要是考虑到即使是相邻地区，经济发展的差异程度不同，两个省份的税收竞争策略互动也不同。经济地理矩阵参照林光平等 （2005）［20］的做法：W∗＝W∗·E，W为普通的地理相邻矩阵，即相邻省份标记为1，不相邻省份标记为0，广东和海南距离较近视为相邻。矩阵E主要描述经济差异情况，， 其中，Eij＝ 0，、代表第i、j个省份2007～2018年的人均GDP。表3中的列 （2）～（4）报告了以经济地理矩阵构建的税收竞争指标的回归结果，核心解释变量的系数符号与基准回归一致，且均是显著的。

因为西部地区的经济发展比较落后，税收竞争比较激烈，本文选取西部地区进行子样本检验。表3中的列 （5）～（7）报告了子样本的回归结果，其中总税收竞争在10%的显著性水平上为负，增值税竞争在1%的显著性水平上为正。所得税竞争的估计系数为负但不显著，这可能是因为西部地区经济发展落后，技术设施不完善，营商环境次于东、中部地区。此时，所得税优惠能够起到招商引资的作用，带动西部地区经济发展，一定程度上缓解了所得税竞争对制造业全要素生产率的抑制作用。

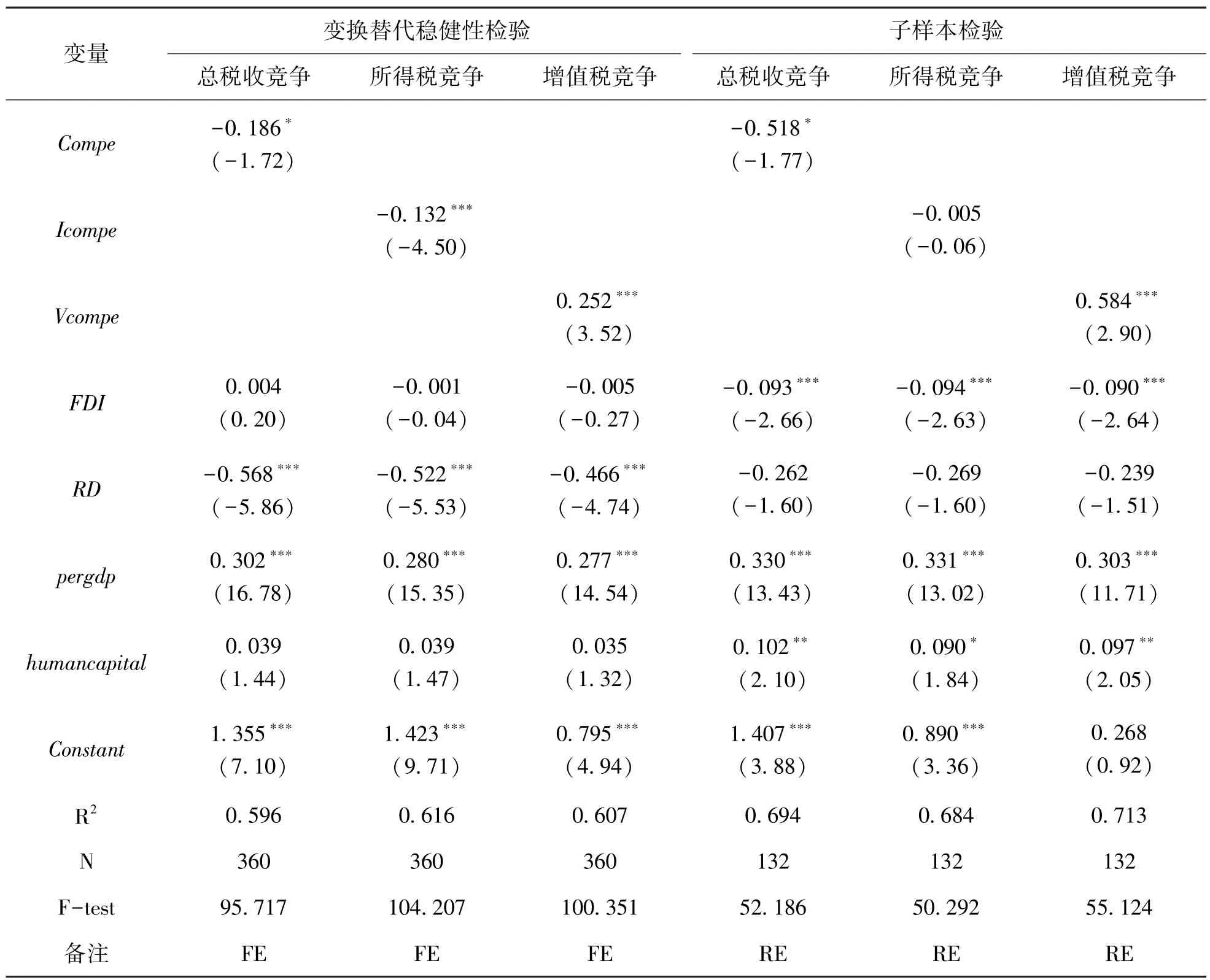
表3 稳健性检验结果

综上，在进行指标替换和子样本的检验后，本文的结论仍具有一定稳健性。

4 进一步讨论：门槛效应分析

4.1 面板门槛模型的设定

由于各个地区的经济发展水平不同，税收竞争的空间及策略有差异，对制造业全要素生产率的影响可能存在非线性关系。据此，本文借鉴Hansen（1999）［21］提出的门槛效应模型，并以人均GDP为门槛变量，构建如下的模型进行实证分析：

5.经营收支结余弥补不正确。如经营收支不匹配，经营结余未进行分配，经营亏损用事业基金弥补。这种处理不符合《事业单位会计制度》的规定。主要是会计人员不熟悉业务导致。

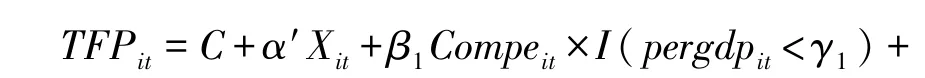
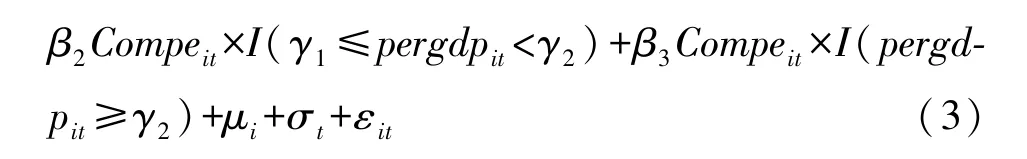
其中，pergdp为门槛变量，代表各地区的经济发展水平，γ为特定的门槛值，I（·）为示性函数，其余变量与 （1）中含义相同。

4.2 门槛效应的检验

利用Stata 14.0软件依次在存在1个、2个和3个门槛的设定下对模型 （3）进行估计，并采用Hansen（1999）［21］的自抽样法进行门槛效应检验，具体的检验结果如表4所示。

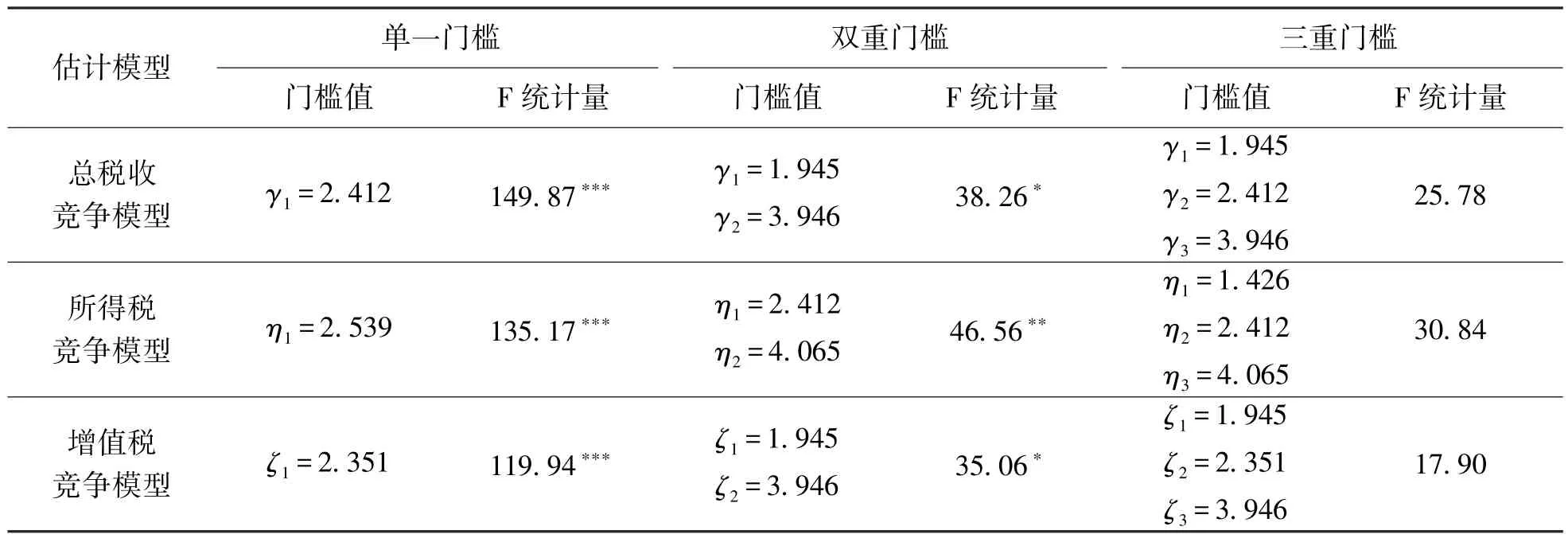
表4 税收竞争门槛估计结果

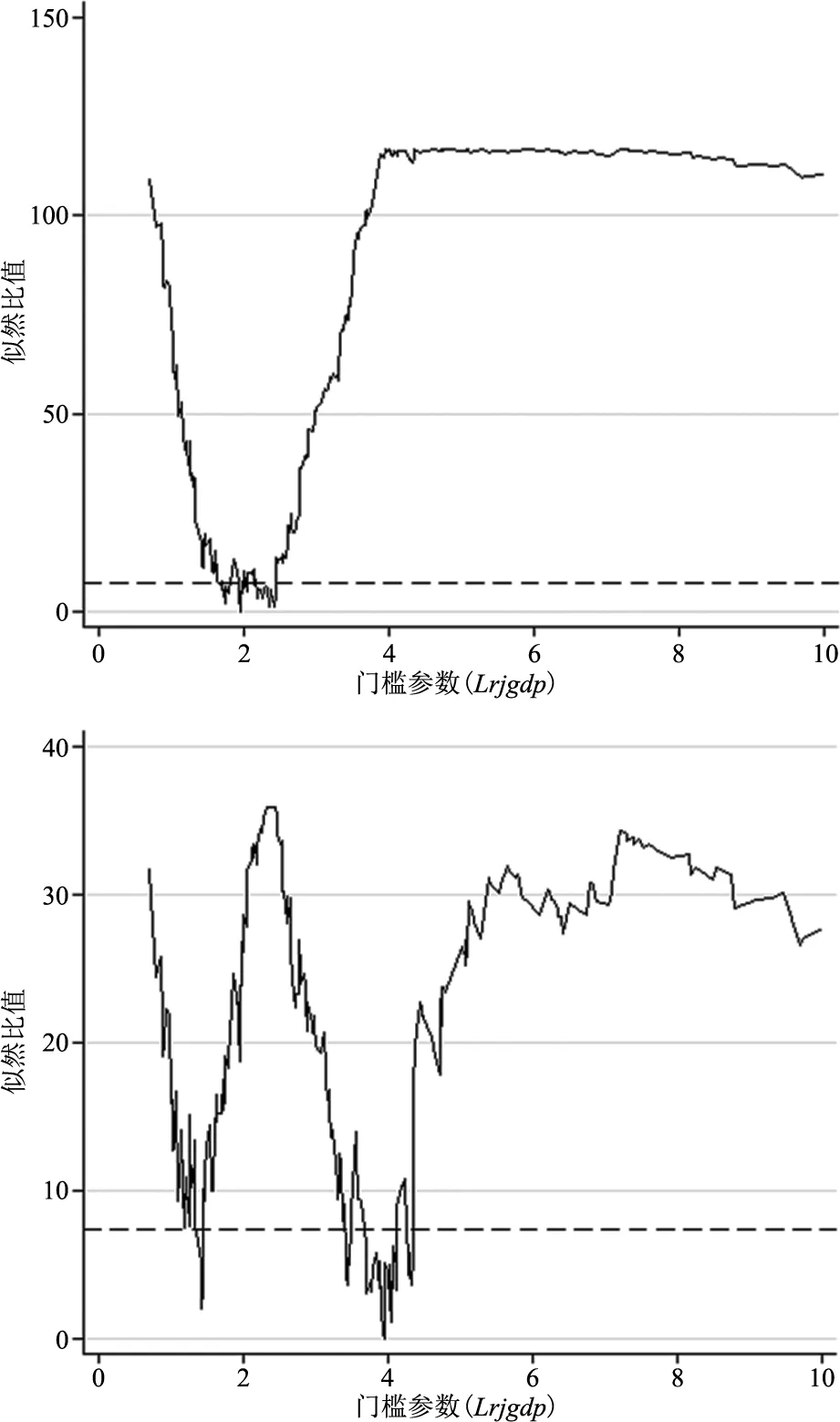
图1 总税收竞争的门槛估计值和置信区间

从表4中可以看出，以人均GDP为门槛变量的总税收竞争、所得税竞争、增值税竞争门槛模型估计中，单一门槛效应均在1%的显著性水平上显著，双重门槛分别在10%、5%、10%的显著性水平上显著，三重门槛效应均不显著，说明3个模型的门槛个数均至少有2个且又小于3个。综上，本文以双重门槛效应模型对总税收竞争、所得税竞争、增值税竞争模型进行相应的估计和分析。

表4中显示，总税收竞争的双重门槛模型的门槛值分别为1.945和3.946，似然比函数图如图1所示，门槛参数估计量是指似然比检验统计量LR为0时γ的取值。因此，总税收竞争门槛估计值可以将样本分成人均GDP小于1.945万元，人均GDP介于1.945万元与3.946万元之间以及人均GDP高于3.946万元3个组别。

所得税竞争的双重门槛模型的门槛值分别为2.412和4.065，似然比函数图如图2所示。因此，所得税竞争门槛估计值可以将样本分成人均GDP小于2.412万元，人均GDP介于2.412万元与4.065万元之间以及人均GDP高于4.065万元3个组别。

增值税竞争的双重门槛模型的门槛值分别为1.945和3.946，似然比函数图如图3所示。因此，增值税竞争门槛估计值可以将样本分成人均GDP小于1.945万元，人均GDP介于1.945万元与3.946万元之间以及人均GDP高于3.946万元3个组别。

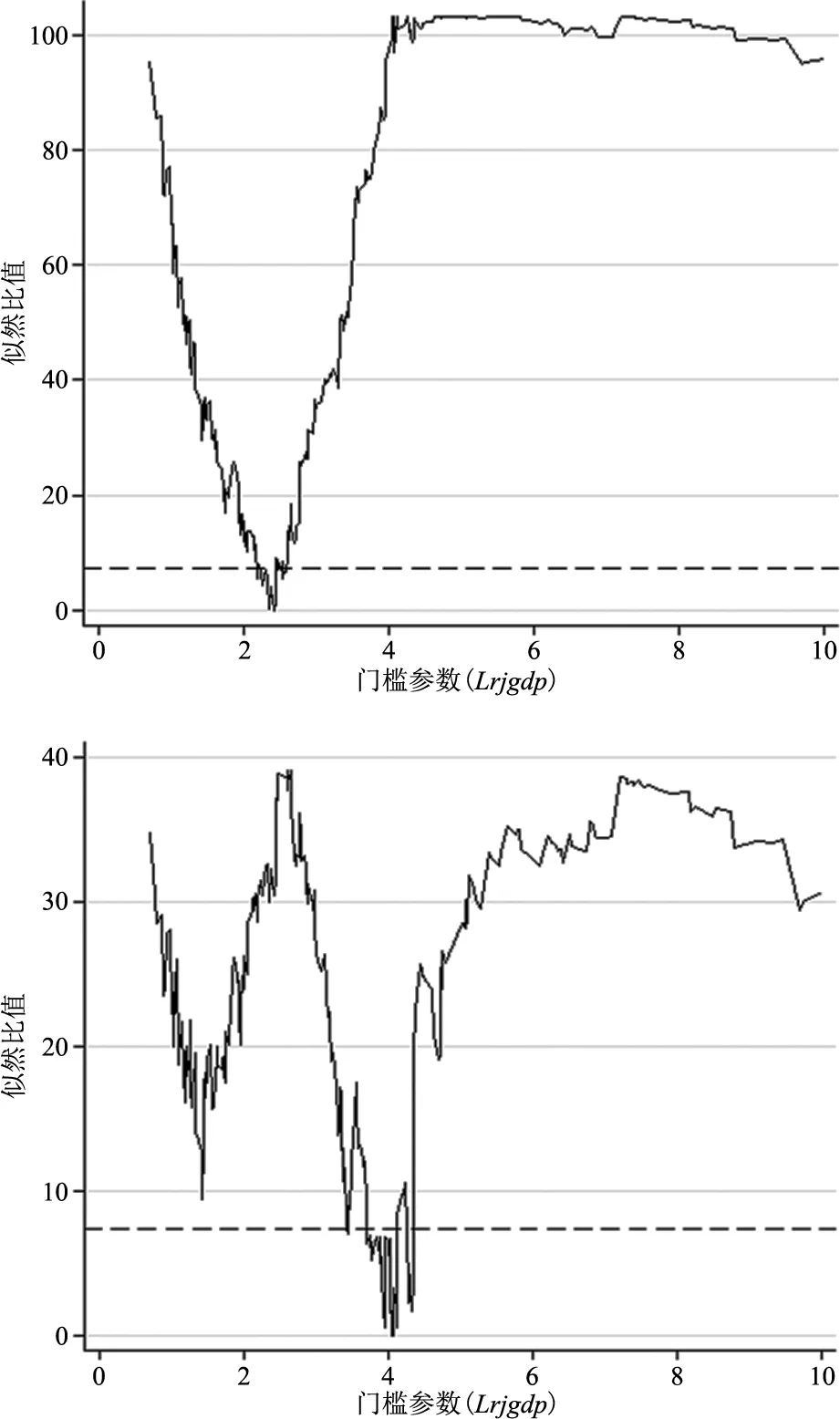
图2 所得税竞争的门槛估计值和置信区间

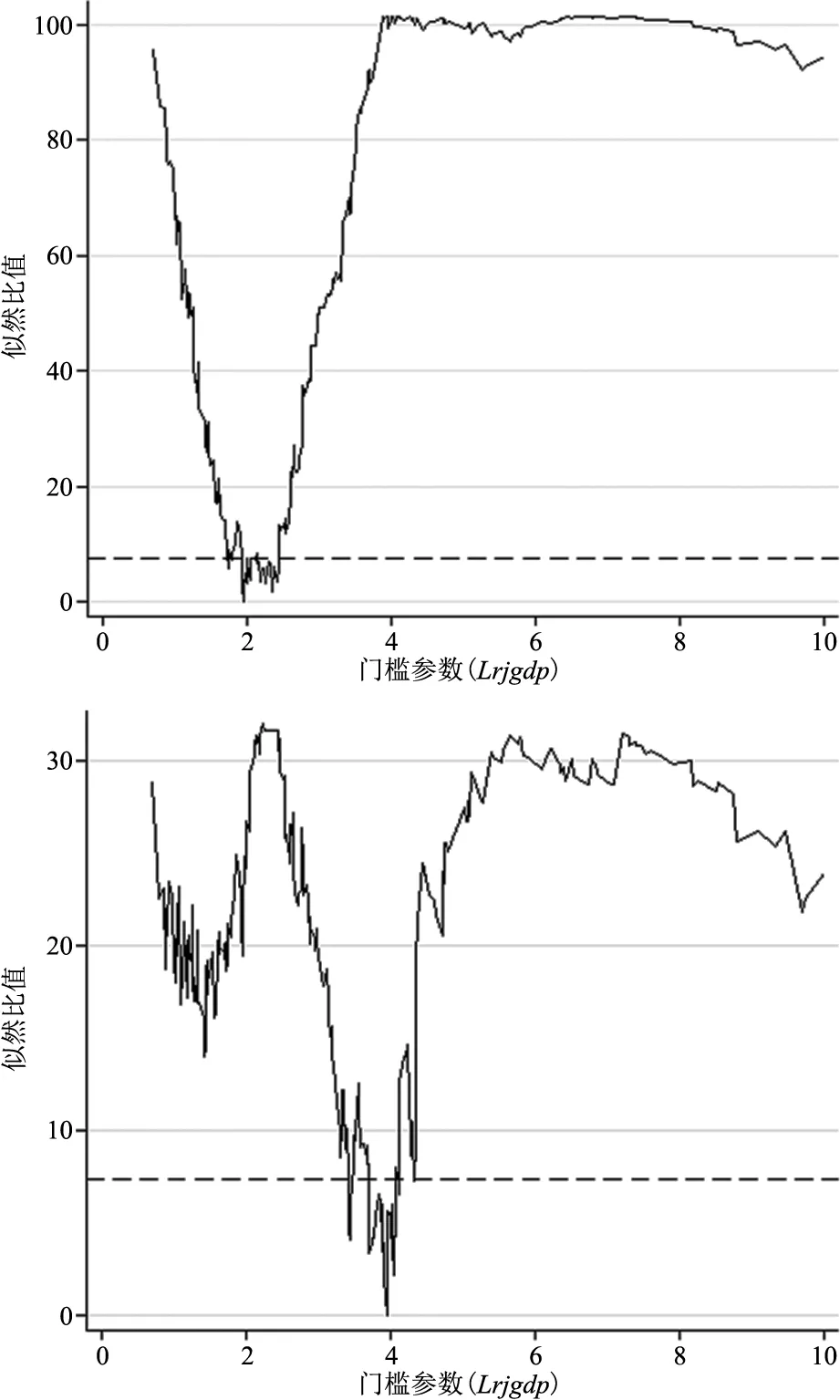
图3 增值税竞争的门槛估计值和置信区间

4.3 模型估计与分析

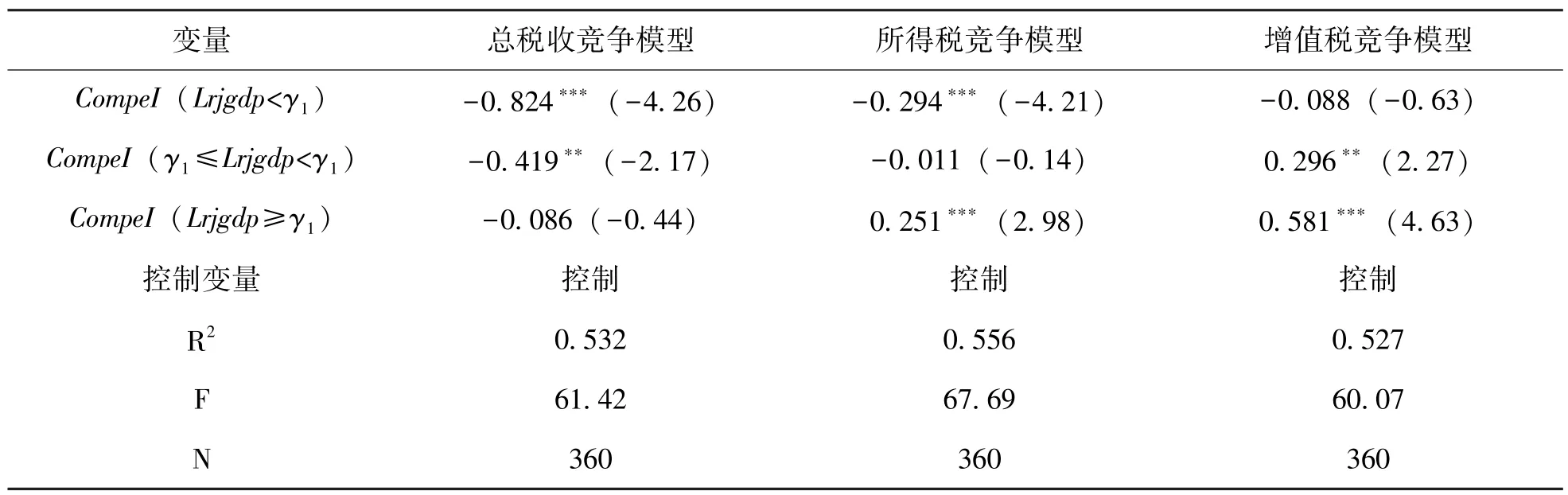
表5 门槛模型的估计结果

从表5的总税收竞争门槛模型的估计结果可以看出，当人均GDP小于1.945万元时，税收竞争的估计系数在1%的显著性水平上为负，当人均GDP介于1.945万元与3.946万元之间时，税收竞争的估计系数进一步减小，在5%的显著性水平上为负。当人均GDP高于3.946万元时，税收竞争的估计系数更小，且不显著。说明在经济发达的地区，总税收竞争对制造业全要素生产率的抑制作用得到缓解，回归结果支持假说2。

由所得税竞争门槛模型的估计结果可以看出，当人均GDP小于2.412万元时，所得税竞争的估计系数在1%的显著性水平上为负。当人均GDP介于2.412万元与4.065万元之间时，所得税竞争的估计系数减小但是不显著。当人均GDP高于4.065万元时，所得税竞争的估计系数在1%的显著性水平下为正。说明经济水平发展到一定程度后，所得税竞争对制造业全要素生产率的作用将由原来的抑制转为促进。

另外，从增值税竞争的门槛模型估计结果可以看出，当人均GDP小于1.945万元时，增值税竞争的估计系数为负但是不显著。当人均GDP高于1.945万元后，估计系数逐渐增大同时显著性水平也逐渐提高。说明随着人均GDP的提升，增值税竞争对制造业全要素的促进作用亦增强。

综上，回归结果支持假说3。

5 结论与启示

5.1 结 论

综合以上实证分析，本文得出如下结论：

（1）从税收总量上看，全国辖区内的总税收竞争不利于制造业全要素生产率的提升。从税收结构上看，全国辖区内的所得税竞争抑制了制造业全要素生产率的提升，但是抑制作用弱于总量上的税收竞争，增值税竞争促进了制造业全要素生产率。

（2）税收竞争对制造业全要素生产率的影响并非线性。总量上的税收竞争对制造业全要素生产率的影响存在双重门槛，随着人均GDP的逐渐提高，抑制作用逐渐减弱。在税收结构上，所得税、增值税竞争对制造业全要素生产率的影响存在双重门槛，当人均GDP超过4.065万元时，所得税竞争对制造业全要素生产率的作用将由抑制转变为促进；当人均GDP超过1.945万元后，增值税竞争的促进作用随着GDP的提升逐渐增强。

5.2 建 议

根据以上结论，提出如下建议：

（1）合理划分中央与地方政府的财权与事权，完善考核机制。过去地方政府财权与事权不对等，在唯GDP的考核机制下，地方政府竞相进行税收竞争，吸引资本投资，实现了经济速度的增长，却忽视了经济质量上的提升。现在，依靠廉价土地、资源消耗的发展方式不再可行，要追求经济的高质量发展，地方政府的考核目标更应该多样化，防止税收优惠的滥用，让我国经济快速踏上高质量发展的道路。

（2）健全增值税优惠政策，规范完善增值税抵扣制度。2016年实施 “营改增”改革后，我国制造业企业增值税税负加重，同时地方政府也失去了营业税这个主税种。2019年10月国务院明确规定保持增值税在央地之间实行五五分享，我国的增值税率相对其他国家仍较高，这意味着地方政府有更大动力及空间在增值税上进行竞争。应该健全增值税优惠政策，规范完善增值税进项税额的抵扣，尽量避免重复征税，有效发挥增值税竞争对制造业全要素生产率的提升作用。

（3）规范税收优惠制度，实行差别化政策。通过本文的实证结论表明，经济发展程度不同的地区，不同税种的税收竞争对制造业全要素生产率的作用不一致。因此，在制定税收优惠政策时，应该防止一刀切，在规范税收政策的同时，应注意结合各个地区的实际情况，制定不同的税收优惠政策，实现制造业全要素的最大幅度提升。