可持续发展视角下工业绿色发展测度及其差异演化

（华北电力大学经济管理系，保定 071000）

引 言

改革开放40年来，工业的跨越式发展为我国经济腾飞做出了重要贡献。但是一味追求经济增长速度，忽视增长质量的粗放式发展方式弊端已经日益显现，资源环境约束开始制约经济发展。陈诗一 （2009）［1］的研究表明改革开放以来消耗了全国67.9%的能源，排放出全国83.1%二氧化碳的工业，其实仅贡献了全国40.1%的经济产出。可见，改变低效的工业发展方式已经迫在眉睫。《中国制造2025》及 《工业绿色发展规划 （2016～2020）》等文件的出台，都标志着我国工业发展进入了绿色转型新时期。十九大报告指出， “坚持在发展中保障和改善民生，增进民生福祉是发展的根本目的。”这就要求经济发展要兼顾环境质量和人类福祉，工业绿色发展测度的指标框架也必须涵盖经济、环境、社会3个方面［2］，以适应可持续发展背景下工业发展的新要求。

随着可持续发展要求的提出，已经有很多学者针对工业绿色发展效率展开研究，数据包络法（DEA）凭借其无需提前设定投入产出函数关系、评价结果客观有效的优势，成为工业绿色发展效率评价的主要方法之一。Song等 （2018）［3］在DEA建模中引入极坐标方法对我国区域环境效率进行评价。 黄磊和吴传清（2019）［4］、 王建民等（2019）［5］和任娇娇 （2019）［6］等学者基于长江经济带的数据展开研究。许学国和张俊杰 （2019）［7］的研究表明我国工业生态效率得分偏低。Yang和Li（2019）［8］研究发现外商投资能促进工业环境效率的增长。Wu等 （2019）［9］发现我国工业部分行业效率低下且发展不平衡。Piao等 （2019）［10］分析了我国省际工业环境效率及其动态变化趋势。可见，DEA方法在工业绿色发展效率的评价方面已获得广泛应用，但是传统DEA方法忽略了生产内部结构对整体的影响，这可能会导致效率测算有偏，而网络DEA弥补了这一缺陷，在测算整体效率的同时也能够评价其子环节效率。万伦来等 （2016）［11］、涂正革和谌仁俊 （2013）［12］以及王兵和罗佑军（2015）［13］等学者采用网络 DEA 方法， 将工业部门的综合效率分解为工业生产效率和环境治理效率，进一步评价我国工业绿色发展水平。但是以上研究中，表征工业绿色发展水平的工业环境效率、工业生态效率及分阶段的环境治理效率，都只包含环境和经济两方面的影响，而可持续发展要求下工业绿色发展的内涵还应当包括工业发展对人类福祉的影响。因此，本文采用Tone和Tsutsui （2014）［14］提出的网络 SBM （NSBM） 模型， 将工业生产过程划分为两个子环节，并在第2个子环节引入代表非经济福利因素的投入产出指标，同时将工业绿色发展效率分解为环境经济效率和环境福利效率。

工业绿色发展效率地区差异也是影响我国工业绿色发展的重要因素，根据 “木桶效应”，工业绿色发展效率较低的地区才是我国工业绿色发展水平提升的关键。对已有文献加以梳理发现，对工业绿色发展水平的地区差异的研究大都集中于定性分析。 Zhang等 （2008）［15］研究发现我国工业生态效率从沿海到内陆呈下降趋势，Wang和Yang（2019）［16］得到了相似的结论。此外，也有学者进行工业绿色发展水平区域趋同研究，σ收敛和β收敛是最常用的研究方法，张子龙等（2015）［17］、申晨等 （2017）［18］和杨宏伟等 （2019）［19］的研究中也采用了相关方法。上述文献对我国工业绿色发展水平地区差异的研究虽已取得一定成果，但还存在以下不足：（1）对我国工业绿色发展水平地区差异的衡量缺乏定量研究；（2）传统σ收敛和β收敛适用于地区内差异的分析而忽视了相邻地域的相互影响。因而本文采用Dagum基尼系数法分析我国工业绿色发展的相对地区差异及其差异来源，并运用Kernel核密度估计法分析绝对地区差异及其动态演变。

与已有研究相比，本文可能做出如下拓展：（1）对工业绿色发展水平进行测度时，在研究框架中加入福利指标的影响，考虑工业发展对人类福祉的影响，更符合可持续发展视角下我国工业绿色发展的要求；评价方法采用网络SBM （NSBM）模型，评价结果更加准确；（2）对可持续发展视角下我国工业绿色发展效率地区差异及其来源进行分析，基于Dagum基尼系数及其子群分析方法展开定量分析，并运用Kernel密度估计分析其动态演变过程。

1 研究方法、变量与数据处理

1.1 研究方法

1.1.1 工业绿色发展效率的NSBM模型

本文采用NSBM模型分析我国工业绿色发展水平，将我国30个省级行政区域的工业生产环节视为决策单元，假定每个决策单元包含两个子环节。在第一阶段，工业部门投入劳动力、资本、能源要素，获得期望产出 （经济发展）和非期望产出 （环境污染），得到环境经济效率；第二阶段，环境污染、医疗支出和环境治理投资作为投入要素，获得最终产出环境治理成效和福利产出，得到环境福利效率；同时得到两阶段综合效率——工业绿色发展效率。在此基础上，构建投入导向、规模报酬不变的NSBM模型如下［20］：

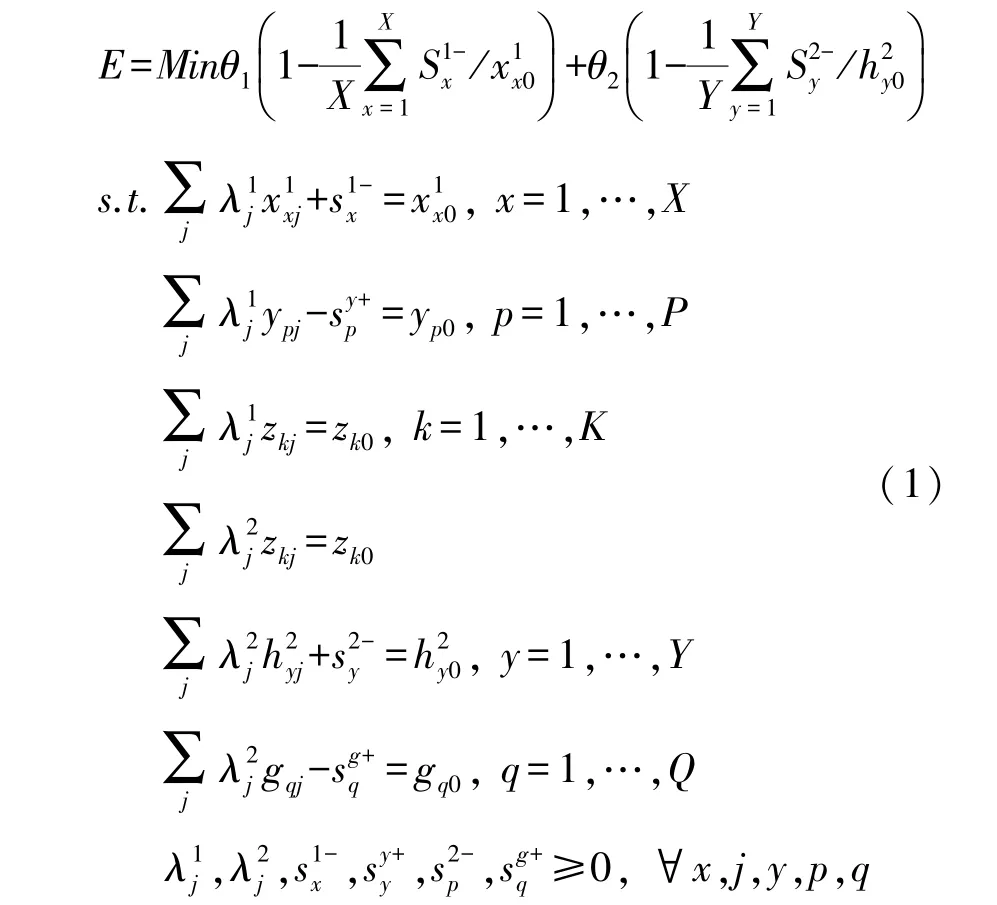
其中，E代表工业绿色发展效率。θ1和θ2代表两阶段的相对权重，在本文中θ1＝θ2＝0.5。X、P和K分别代表第一环节投入变量、期望产出和非期望产出个数，Y和Q分别代表第二环节额外投入变量个数和最终产出变量个数，本文中对应取值分别为：X＝3、P＝1、K＝1、Y＝2、Q＝2。相应地，x、y和z分别代表第一环节的投入变量、期望产出和非期望产出 （中间产出）；h和g分别代表第二环节的额外投入变量和产出变量。和表示权重变量，代表松弛变量。

1.1.2 Dagum基尼系数及其子群分解方法

本文采用1997年 Dagum［21］提出的 Dagum基尼系数及其子群分解方法来分析可持续发展视角下我国工业绿色发展水平的地区差异及其来源，基尼系数定义如式 （2）：

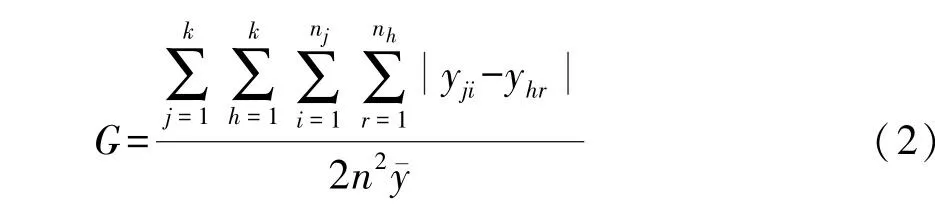
其中，k代表所划分的区域个数，本文依据传统三大经济区域的划分方法，将我国划分为东、中、西部3个区域，故k＝3；j和h分别为3个区域中的不同地区；nj和nh分别代表地区i和地区r中的省份个数；n是研究样本中所有省份个数，本文中n＝30；yji代表地区j中第i个省份的工业绿色发展效率；yhr代表区域h中第r个省份的工业绿色发展效率；代表我国30个省份工业绿色发展效率的平均值。

Dagum基尼系数及其子群分解方法将总体基尼系数G分解为地区内差距贡献Gw、地区间净值差距贡献Gnb和超变密度贡献Gt，并满足G＝Gw+Gnb+Gt。

1.1.3 Kernel密度估计

Kernel密度估计是一种基于核函数刻画连续的密度曲线，以对随机变量的动态分布进行直观描述的非参数方法，常用于绝对地区差异分析。密度函数定义如下：

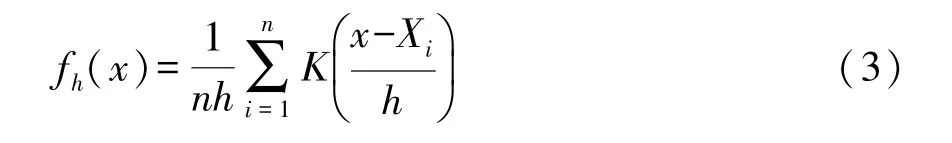
式中：K（·）为核函数，h为带宽。

本文选用高斯核函数分析可持续发展背景下全国及三大区域的工业绿色发展效率动态演变规律。

1.2 变量及数据处理

参考已有研究指标体系构建原则，考虑数据的可获得性，本文选取2003～2018年我国30个省级行政区域 （西藏及港、澳、台地区除外）的面板数据进行研究。原始数据来源于 《中国统计年鉴》、《中国环境年鉴》、《中国卫生年鉴》、《中国城市统计年鉴》和国家统计局，极少数缺失数据通过内插法和外推法得到。

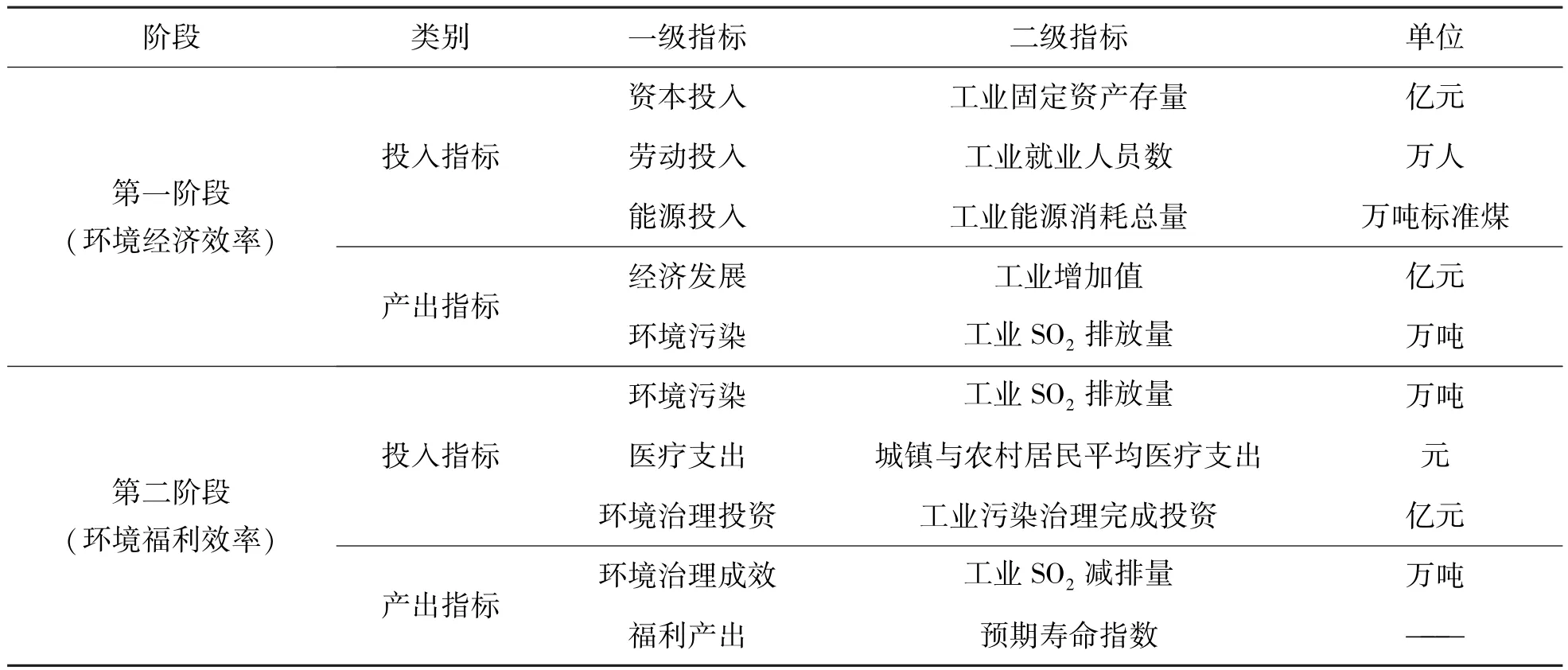
表1 基于NSBM方法的工业绿色发展效率评价指标体系

2 实证结果分析

2.1 工业绿色发展效率及其分阶段效率

2.1.1 工业绿色发展效率

表2列出了我国30个省级行政区域2003～2018年间工业绿色发展效率及排名情况，由于文章篇幅限制，仅展示所有单数年份及2018年的效率测算结果。

整体来看，16年间我国工业绿色发展效率的平均值为0.747，未能实现DEA有效，还存在较大的提升空间。样本期间，效率值呈 “M”型波动式增长特征，两个高点出现在2006年和2012年，尤其是2012年，达到了16年中的最高点。

从省际来看，贵州、北京、重庆3省 （市）的效率值在样本中排名前3，平均值均大于0.9，远高于全国平均水平。作为全国的经济、政治中心和中国的名片，北京的工业绿色转型开始较早且成果显著。 “山城”重庆，以旅游城市的身份走上绿色发展道路。相比之下，贵州省不具备地理条件和经济条件的优势，但其以资源深加工和特色轻工业为主的特色产业结构和对基础医疗投入等基础保障的重视奠定了其福利效率的增长基础，16年间贵州省每千人中，医疗人员数量增幅达到了275%，是北京增幅的2.43倍。排在后3位的依次是吉林、浙江、黑龙江，效率值均低于0.6，远低于全国的平均值。黑龙江和吉林作为我国老工业基地的代表地区，受结构性、体制性矛盾等历史遗留问题的影响，传统发展方式未能实现有效创新，发展方式的新旧对接问题是造成相关省份效率较低的主要原因，而浙江省需要增强工业发展对人类福祉影响的重视程度，促进其环境福利效率的提升。

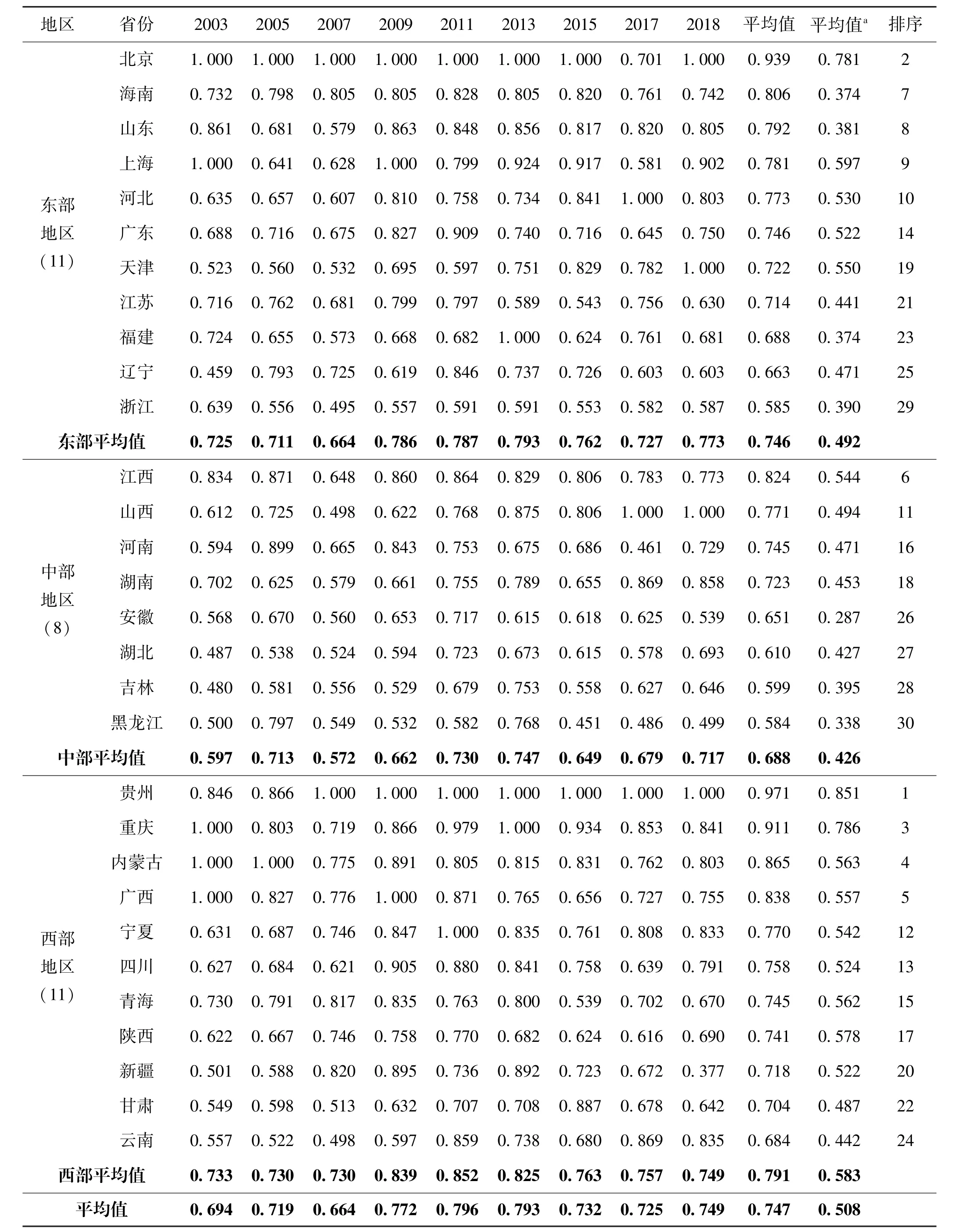
表2 2003～2018年我国工业绿色发展效率

从区域层面来看，三大区域呈现 “西部最高，东部次之，中部最低”的分布格局，西部地区的平均值为0.791，远高于全国平均水平，东部和中部的均值都低于全国平均水平，各区域的工业绿色发展水平和经济发展水平呈现一定的矛盾关系。早期粗放式发展造成的环境破坏、资源浪费及如今主导产业向第三产业转移是东部地区工业绿色发展效率偏低的主要原因。而西部地区虽然经济水平暂时落后，但是 “西部大开发”等战略保障，西部地区的资源优势以及日益成熟的工业生产技术，都为西部地区工业绿色发展提供了强有力的支持。

此外，本文还测算了未考虑福利因素时的工业发展效率 （见表2平均值a），对比可知，在未考虑福利因素时，效率值被低估，在考虑福利因素的影响后，效率值整体上有较大提升，并且更加符合现阶段绿色发展要求下各地区工业发展的实际情况。

2.1.2 工业绿色发展效率的解构

效率解构结果表明环境福利效率明显低于环境经济效率 （如图1），环境福利效率偏低是导致我国工业绿色发展水平不高的主要原因。综合两阶段的效率表现可以看出，北京、贵州等地在工业生产的两个子环节中均表现良好，是我国工业绿色转型的先行者，基本实现了经济、社会、环境协调发展，在未来的发展中应进一步巩固其环境治理和人类福祉提升方面的优势地位，为其他地区的发展提供借鉴。内蒙古、广东、天津等省份在工业生产的经济效率方面表现良好，环境福利效率是制约其工业绿色转型实现的瓶颈因素，在未来的发展中应当增加在教育、医疗、基础设施等方面的投入，促进福利水平和工业经济协调发展。海南、江西等省份的环境福利效率较高，生产技术落后导致的环境经济效率过低是该类地区发展的制约因素，加大对技术创新和环境治理的重视程度，促进环境经济效率的提升是该类地区发展的首要任务。此外，以辽宁、吉林、黑龙江等老工业基地为代表的地区，环境经济效率和环境福利效率均处于较低水平，相关地域不能适应可持续发展的要求，在注重工业发展水平提升的同时还要加大教育和医疗投入，在实践中追寻环境经济效率和环境福利效率共同提高。

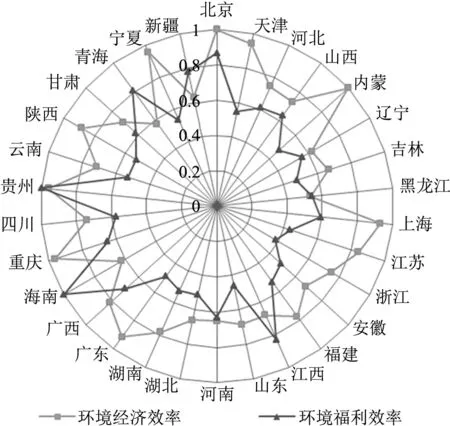
图1 分阶段效率测算雷达图

2.2 工业绿色发展效率区域差异分析

2.2.1 基尼系数及其分解

从总体基尼系数来看，16年间，工业绿色发展效率的总体基尼系数呈 “W”型下降趋势，说明可持续发展要求下工业绿色转型的地区发展不平衡状况有好转趋势。从基尼系数的变化可以看出，16年间总体基尼系数的两次上升分别出现在“十一五”规划的开局之年和 “十二五”规划的收官之年，可见新政策的出台或者即将迎来的政策变动会影响企业决策，从而导致工业绿色发展区域差异产生扩大趋势。进入21世纪以来，不同时期我国工业发展的具体政策不同，但是可持续发展的中心思想一以贯之，因此整体来看，全国范围内工业绿色转型发展的不均衡现象日渐缓和。

从地区内基尼系数来看，三大经济区域地区内差异均呈波动变化特征，整体而言，东部地区内差异最大，中部次之，西部地区内差异最小。样本期间，东部和西部地区的基尼系数不断减小而中部地区基尼系数逐渐增大。具体来看，东部地区基尼系数年均下降0.15%；西部地区内工业绿色发展效率的基尼系数呈倒 “U”型变化，年均下降0.21%，可见西部地区区域内差异减小程度更大；中部地区内基尼系数增大，呈 “W”型变化特征，地区差异年均增长率为0.11%，自2016年起，中部地区工业绿色发展效率地区内基尼系数成为三大区域中最大的，可见一味追求经济发展，将导致工业绿色转型进程中区域内差距进一步扩大。

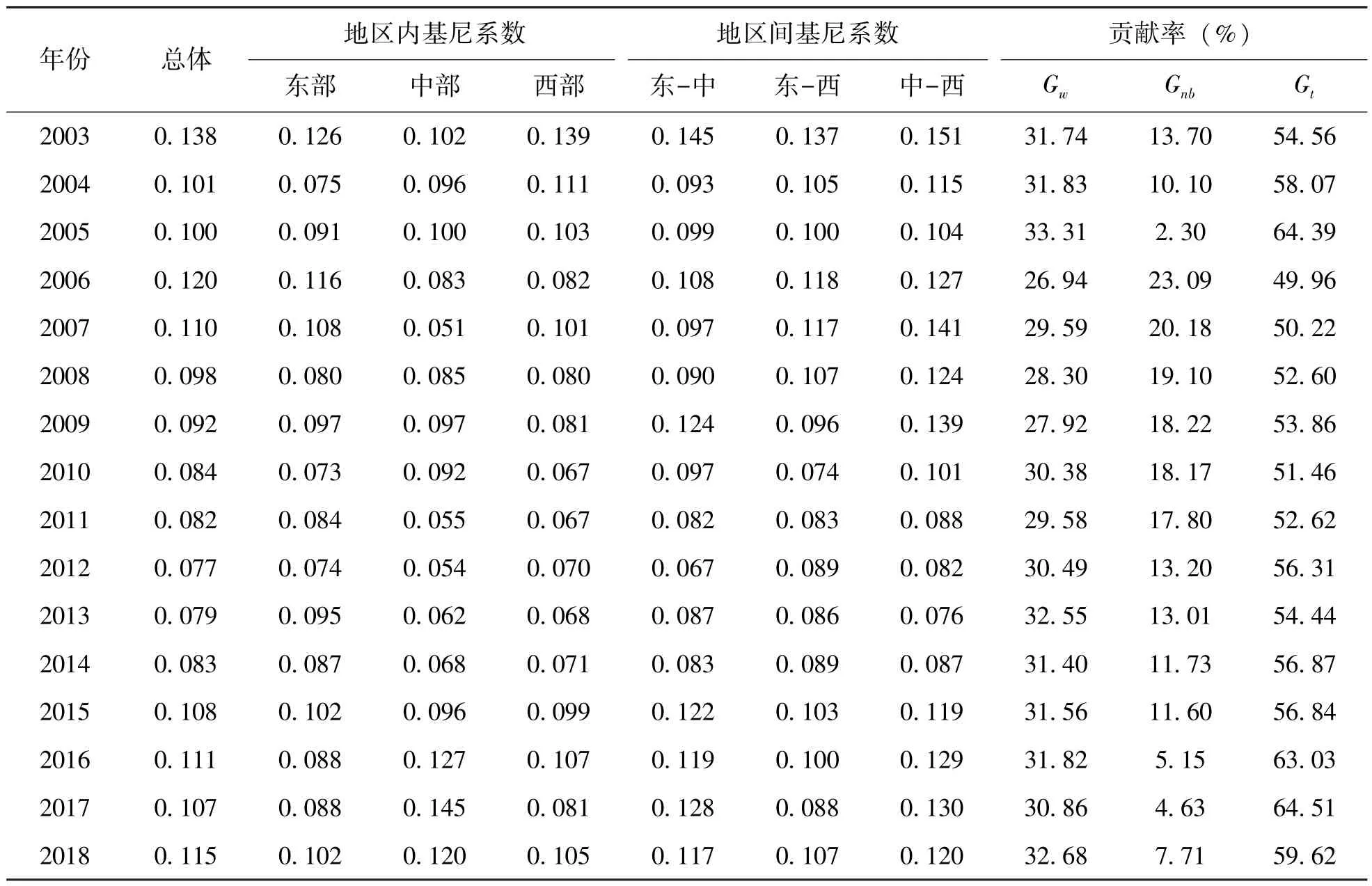
表3 2003～2018年工业绿色发展效率的地区差异分解及其来源

从地区间基尼系数来看，工业绿色发展效率区域间差异均呈下降趋势，其中东-西部下降程度最大，下降百分比达21.9% （以2003年为基期），虽然发生变化的时间点不完全一致，但考察期间变化基本一致。说明16年间工业绿色发展效率区域间差异减小，工业绿色发展水平逐渐趋于一致。具体而言，2003～2011年，中-西部地区间基尼系数最大；2012～2014年，东-西部区域间基尼系数最大；2015年，东-中部区域间差异最大；2016～2018年，中-西部区域间基尼系数最大。

从区域差异贡献率及其来源看，超变密度贡献率最高，均值达到56.21%，其次是区域内差异的贡献率，区域间差异贡献率最低。从具体变化来看，区域内差异贡献率较为平稳，维持在30%左右，说明从单个区域内部来说，工业绿色发展水平整体上较为稳定，可能存在 “俱乐部收敛”。超变密度贡献率的变化和区域间差异贡献的变化恰好相反，且超变密度贡献率远高于区域间差异，可见超变密度是导致我国工业绿色发展效率地区差异的主要来源，地区间的交叉重叠现象凸显，即虽然西部地区效率值高于东部地区，但西部地区某些工业绿色发展水平较低的省 （市）其效率值可能低于东部地区工业绿色转型发展较好的省 （市），超变密度贡献率的不断提升，表明这种交叉重叠现象愈演愈烈，工业绿色发展效率的地区间差距呈现缩小趋势。

2.2.2 核密度估计

为进一步分析不同地区工业绿色发展效率在样本期间的变化过程，采用核密度估计分析其动态演变过程。从图2可以看出，在观测期内，全国及三大区域中，核密度函数中心均在一定程度上向右移动；函数峰值和曲线形态也有一定的变化；此外，极化现象也经历了不同的变化过程。表明工业绿色发展效率随时间变化有一定程度的提高，区域差异也不断变化。此外，各区域核密度曲线的分布形态也各有特点。

随着时间变化，全国工业绿色发展效率的Kernel密度曲线的右尾形态逐渐消失，密度函数中心右移，说明在全国范围内工业绿色发展效率日益提升，同时区域差异日渐减小，效率的两级分化现象逐渐消失。此外，函数中心 “先右移，再左移”的变化轨迹表明工业绿色发展效率波动上升的变化特征。

东部地区工业绿色发展效率的Kernel密度曲线的多峰形态越来越明显，说明区域内开始显现微弱的多级分化现象，右尾形态的出现说明工业绿色发展水平的提高，区域内部分省份间出现了高值集聚。

中部地区工业绿色发展效率的Kernel密度曲线主峰高度先 “大幅上升”而后 “逐步回落”，是研究范围中主峰高度唯一降低的区域，主峰宽度则经历了 “小幅收窄-显著变大”的过程，而函数密度中心变化幅度微弱，意味着中部地区效率值变化不大，但是各省份间的差距逐渐增大，阶梯分化现象日益凸显。

西部地区工业绿色发展效率的Kernel密度曲线函数密度中心向右移动的幅度最大，密度曲线形态由双峰逐渐演变成单峰，主峰高度先 “显著上升”而后 “小幅下降”，说明样本期间内西部地区的效率值有明显提高，工业绿色转型发展良好，并且区域内的两极分化状况逐渐消失，区域内各省 （市）工业发展相互促进，工业绿色发展水平逐渐趋于一致。

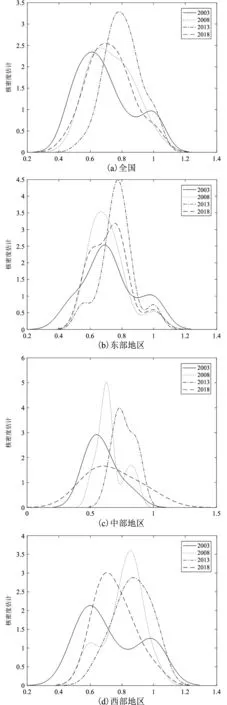
图2 工业绿色发展效率核密度估计

3 结论与政策建议

本文采用NSBM模型研究可持续发展要求下我国工业绿色转型发展情况，从经济、环境、社会3个角度出发选取投入产出变量，创造性地加入了福利因素的影响，将工业生产过程划分为两个子环节，同时将工业绿色发展效率分解为环境经济效率和环境福利效率，并利用工业绿色发展效率来表征我国工业绿色发展水平。随后，运用Dagum基尼系数及其分解方法分析了我国工业绿色发展效率的地区差异及其来源。在此基础上，利用Kernel密度估计法分析其分布的动态演进规律。具体结论如下：

（1）从效率测算结果来看，工业绿色发展效率整体水平偏低，未实现DEA有效，观测期内呈“M”型增长态势，绿色发展效率解构结果表明环境经济效率远高于环境福利效率，实现我国工业绿色转型的关键在于环境福利效率的提升。从区域层面来看，工业绿色发展效率区域差距显著，三大区域呈现 “西部最高，东部次之，中部最低”的阶梯分布特征。从省域层面来看，工业绿色发展效率的省际差异悬殊，贵州、北京、重庆3省（市）的效率值在所有样本中排名前3，吉林、浙江、黑龙江3省排在后3位。

（2）从地区相对差异来看，全国范围内工业绿色发展效率总体差异呈 “W”型下降趋势。从区域内差异来看，东部的地区内差距最大，中部地区次之，西部地区内差距最小；东部和西部的地区内差异逐渐减小，中部地区各省份间的差距进一步扩大。从地区间差异看，工业绿色发展效率的地区间差距均呈不同幅度的缩小态势，中-西部地区间差距最大，而东-西部的地区间差距最小。对差异来源及其贡献的分析发现，超变密度贡献率最高且不断上升；区域内差异贡献率次之且较为稳定；区域间差异贡献率最低且呈下降趋势。

（3）从动态演进特征来看，全国及三大经济区域工业绿色发展效率呈现波动上升态势，地区间发展不均衡现象各有变化。全国范围内，区域差距逐渐减小，两极分化现象逐渐消失；东部地区开始显现多级分化态势，逐渐出现高值集聚；中部地区分化现象日益显著，区域差距逐渐扩大；西部地区效率分布阶梯化现象逐渐消失，工业绿色发展水平趋于一致。

基于以上结论，提出如下政策建议：

（1）重视工业发展对人类福祉的影响，以提高环境福利效率为出发点，促进工业绿色转型。区域工业绿色发展水平与经济发展水平的矛盾表明，虽然中、西部地区当前工业生产水平稍低，但却具有极大的绿色环境生态资源优势，发展以增进民生福祉为目的的绿色产业，将中、西部地区的潜在优势转化为绿色生产力是工业绿色转型的必然要求。

（2）合理引导产业转移，推进跨区域产能合作。我国工业绿色发展水平不一，省域间差距悬殊，不同地区经济条件、技术水平、资源禀赋、政策条件等方面存在不同的优势条件，均为跨区域产业合作提供了可能。应基于不同地区的优势条件，对产业转移加以引导，促进跨区域产业带和工业产业园区的形成，缩小区域差距，实现工业绿色发展水平的共同提升。