微观企业全要素生产率及其增长率测算方法综述

（中国人民大学统计学院，北京 100872）

引 言

目前，中国经济面临着人口红利消失、资本累积速度下降等问题，增速放缓，由高速增长向高质增长的转型将成为经济发展的必然选择。相比于扩大要素投入量，提升全要素生产率 （TFP，Total Factor Productivity）才是实现高质量发展的关键所在。微观企业作为国民经济的细胞，科学测算其TFP及TFP增长率，可以从根本上把握经济发展质量，为我国经济由粗放式增长转为集约式增长提供重要参考。

近年来，信息技术的飞速发展使得微观数据获得性增强，国内外涌现出大量关于企业TFP及其增长率的测算研究。与国家宏观或行业中观层面的测算相比，企业微观层面的测算更多地考虑了自身的生产决策，体现了不同的经济理念。因此，对企业TFP及其增长率测算方法进行综述，有助于研究者明确适用于企业层面的测算方法，避免实证分析中的误用。

已有学者对企业层面TFP及其增长率的测算方法进行梳理。Van Biesebroeck（2007）梳理了企业TFP测算中常用的非参数方法，使用模拟数据对不同方法的稳健性进行分析［1］。Beveren（2012）梳理了企业TFP测算中常用的参数和半参数方法，使用比利时食品公司数据对不同方法进行实证研究［2］。鲁晓东和连玉君 （2012） 梳理了企业TFP测算中主要的参数和半参数方法，使用我国工业企业数据横向对比各方法的优劣［3］。柳狄和尹恒 （2015）梳理了企业TFP测算的传统方法和结构方法［4］。张志强 （2015） 梳理了尝试解决联立性偏误等问题的企业TFP测算方法，通过蒙特卡洛模拟比较各种方法的优劣［5］。王健和胡美玲（2019）梳理了尝试解决联立性偏误、样本选择偏误、遗漏价格偏误以及企业多产品产出等问题的企业 TFP 测算方法［6］。

目前关于企业TFP及其增长率测算方法梳理的文献，或者将测算方法区分为参数方法、半参数方法和非参数方法，或者将测算方法区分为增长核算法和计量经济学方法，或者将测算方法按照其尝试解决的问题进行区分，而忽视了区分各方法的本质思想。此外，许多研究并没有明确区分TFP和TFP增长率，这两者虽然有一定的相近性，但仍然有不同的侧重点和政策作用。就概念而言，TFP通常是指广义的技术水平，包括要素质量、管理水平、技术使用效率、规模效应等因素，反映企业在某一时点上的综合生产效率，而TFP增长率通常指广义的技术进步水平，如要素质量的提升、管理水平的改进、技术使用效率的提高等，反映企业某一时点综合生产效率相比于另一时点的提升；就效应而言，企业短期内的竞争力主要受综合生产效率的影响，而生产效率水平的增长则是保障企业竞争力的根本原因；就测算方法而言，不同方法在测算生产率和生产率增长率方面各有优缺点。对这两者测算方法的混用将导致不能准确把握企业的生产经营状态，从而不能有的放矢，更好地促进企业发展。

因此，本文在梳理各种测算方法时，区分TFP和TFP增长率概念，基于全新的视角，将企业TFP及其增长率测算方法按照隐藏的思想内涵，归类为基于 “余值”思想的方法和基于 “生产前沿面”思想的方法，为以后更好地测算企业TFP及其增长率提供基础。

1 基于“余值”思想的测算方法

1957年，Solow假设技术进步满足希克斯中性，基于如下形式的生产函数，尝试找到美国经济增长的原因［7］：

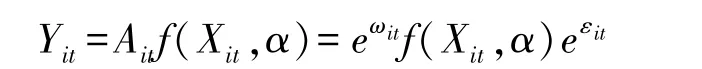
其中Yit和Xit＝（Xit1，Xit2，…，Xitn）′分别为生产单元i在时期t的产出和要素投入向量；α＝（α1，α2，…，αn）′为各要素对应参数组成的向量；Ait＝eωiteεit为除生产要素外其他所有影响产出的因素。Solow认为式 （1）：

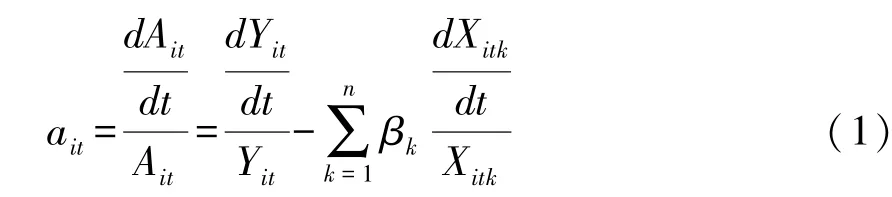
即为生产单元i在时期t的TFP增长率，其中为第k种生产要素的产出弹性。

ait即为著名的 “索洛余值”，可以被进一步分解。 令由式 （1） 可得式 （2）：

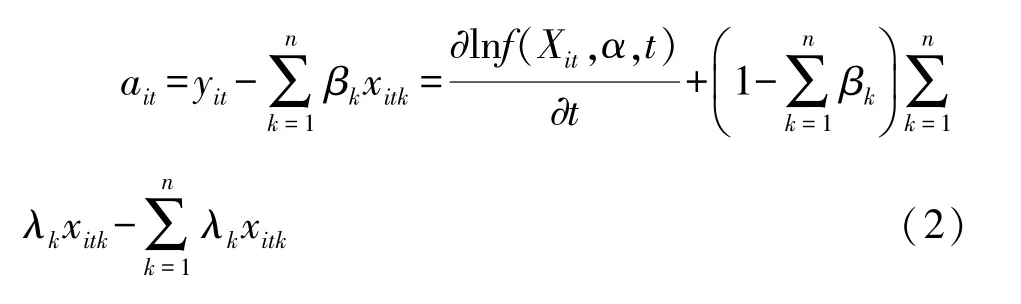
Solow的 “余值”思想对TFP增长率的测算做出了开创性的贡献，也启发研究者将 “余值”思想与TFP测算相结合，认为就产出而言，扣除生产要素投入量的影响，剩余部分都可以归因于TFP， 式 （3）：

即为TFP。

基于 “余值”思想测算企业TFP及其增长率：选取合适的生产函数之后，对其两端取对数即为生产要素对产出的回归方程，估计参数向量α，由式 （3）和 （1）即可分别得到企业TFP及增长率。传统的参数估计方法为最小二乘法，由于企业异质性以及相关数据获取的限制性，该方法通常会遇到内生性、样本选择偏误、价格指数影响效应、多产品与单一产品等因素导致的参数识别问题。为了克服这些问题，学者们引入了工具变量法、固定效应模型、动态面板模型和结构模型等来测算企业TFP及其增长率。

1.1 工具变量法

工具变量法主要解决参数估计中的内生性问题。许多研究将要素投入价格作为工具变量，因为其与要素投入量高度相关，但由要素市场决定，故不受企业对自身TFP水平认知的影响。但Ackerberg等 （2007）指出，要素价格易受市场势力的影响，不完全竞争的要素投入和产出市场将导致要素价格失效［8］。此外，企业通常将雇员平均薪资作为劳动要素的投入价格，但是雇员平均薪资通常与他们的技术水平相关，而雇员技术水平通常会影响企业TFP水平，这也将导致要素价格与ωit的相关性。

除了要素价格之外，其他一些可以影响要素供应或产出需求的变量也可以作为工具变量，比如天气、资本或劳动市场的外生冲击等。尽管这些变量可能更难获得，但相比于要素价格，它们不易受企业市场势力的影响。但Ackerberg等 （2007）也指出，如果这些变量与样本的选择偏误有关，那么工具变量也将失效［8］。

1.2 固定效应模型

Mundlak（1961）和 Hoch（1962）将固定效应模型引入了经济学领域，之后学者们尝试使用这种方法来估计生产函数参数，进而测算企业TFP［9，10］。固定效应模型假设对指定企业而言，ωit在样本期内保持不变，此时估计方程变为lnYit＝ωt+αlnKit+βlnLit+εit。对该式进行一阶差分可以从方程中消除ωit，因此在一定程度上解决了OLS的内生性问题。由于企业的退出决策通常取决于其自身TFP水平，因此固定效应模型也在一定程度上减弱了OLS的样本选择偏差问题。固定效应估计对ωit跨时不变的假定比较苛刻，有点脱离实际，因此在实证研究中有时表现得并不尽如人意，Griliches和Mairesse（1998）指出固定效应方法经常会低估资本产出弹性［11］。

1.3 动态面板模型

动态面板模型可以看作是固定效应模型的拓展，主要尝试解决生产函数参数估计中的内生性问题。动态面板模型假设ωit＝θi+γit，将企业TFP分为样本期内保持不变的部分和样本期内发生变化的部分。θi一般由市场势力等因素决定，而γit经常由需求或供给冲击等导致，此时估计方程变为 lnYit＝θi+γit+αlnKit+βlnLit+εit。 Arellano 和 Bond（1991）假设γit不存在自相关，对上式进行一阶差分， 并将滞后 2 期及以上的生产要素Li，t-τ，Ki，t-τ（τ≥2）作为工具变量，使用差分GMM方法对差分方程进行参数估计［12］。 Blandell和Bond （1998）假设γit存在一阶自相关，对上式进行二阶差分，并使用滞后 2 期及以上的生产要素Li，t-τ，Ki，t-τ（τ≥2） 和滞后 3期及以上的产出Yi，t-τ（τ≥3） 作为工具变量，使用差分GMM方法对差分方程进行参数估计［13］。但以上两种方法均存在弱工具变量问题，模型在蒙特卡洛模拟和实际运用中的表现均不太理想。Blandell和Bond（2000）在差分GMM方法的基础上，建议进一步使用差分变量滞后项作为生产要素和产出等水平值的工具变量，使用系统GMM方法同时估计差分方程和水平方程［14］。系统GMM方法使用了更多的工具变量，因此在一定程度上解决了水平值滞后项的弱工具变量问题，提高了估计效率，在研究中运用较为广泛。

1.4 结构模型

工具变量法、固定效应模型和动态面板模型在估计参数时都忽略了生产过程中企业的行为和决策信息。但企业生产活动很大程度上取决于自身的行为与决策结构，在测算时充分考虑这些信息，结果才更可靠。Olley和Pakes（1996）最早在测算中考虑企业决策行为，尝试打开企业生产经营的黑箱，该模型通常被称为OP模型［15］。OP模型及其一系列的改进模型统称为结构模型，是当前估计微观生产函数进而测算企业TFP的一种主流方法。

1.4.1 OP模型

OP模型的基本思路是使用可观测的企业投资作为不可观测的TFP的代理变量来解决内生性问题，使用企业价值最大化的Bellman方程和生存概率来确定企业的退出准则，进而解决样本选择偏误问题。OP模型假定市场结构由各企业状态变量所决定；各企业投入要素价格相同且均服从外生的一阶马尔科夫过程；市场投资满足马尔科夫最优纳什均衡，即企业对未来市场结构的预期与它们的选择所导致的市场结构将最终一致，Bellman方程中涉及到的企业收益函数和价值函数形式取决于市场结构和投入要素价格，因此纳什均衡下各企业有相同形式的收益函数和价值函数，保障了Bellman方程的引入。

具体而言，OP模型设定生产函数的对数形式为：

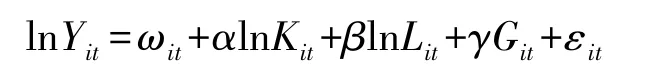
其中，劳动要素Lit为可以随时调整的自由变量，其投入受当期ωit的影响，不受企业资本要素Kit的影响，同时也不影响企业TFP和投资；资本要素Kit、企业年龄Git以及ωit为状态变量，ωit服从外生的一阶马尔科夫过程，Kit和Git受到E［ωit｜Ji，t-1］和ωi，t-τ（τ＝1，2，…） 的影响， 其中Ji，t-1为t-1期的信息，包括企业的要素投入和生产率等；企业当期资本取决于上期资本和投资，与当期投资无关， 即Kit＝k（Kit-1，Iit-1）； 企业投资取决于企业年龄、 当期资本和 TFP 水平， 即Iit＝i（ωit，Kit，Git）。

Pakes（1994）证明了当企业投资不为零时，i（ωit，Kit，Git）是ωit的严格递增函数， 因此有ωit＝ω（Iit，Kit，Git）［16］。 令φit＝φ（Iit，Kit，Git）＝αlnKit+γGit+ω（Iit，Kit，Git）， 此时生产函数的对数形式变为式 （4）：

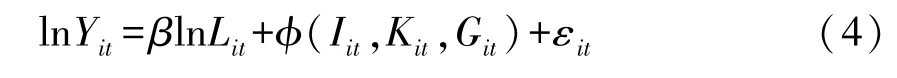
同时Olley和Pakes（1996）考虑企业的退出行为，并推导出企业当期的生存概率由企业上期的年龄、投资以及资本存量决定，即Pit＝P（surviveit＝ 1）＝p（Ii，t-1，Ki，t-1，Gi，t-1）， 此时生产函数的对数形式也可变为式 （5）：

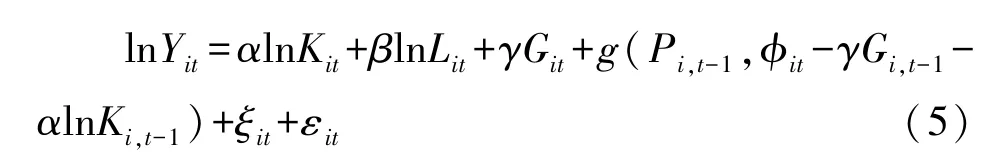
其中ξit＝ωit-E（ωit｜ωi，t-1，surviveit＝1）为时期t企业TFP受到的随机冲击，与企业t期的状态变量不相关， 即E（ξitKit）＝E（ξitGit）＝ 0。

OP方法的参数估计过程可以分为3步：（1）估计劳动系数β。使用核估计或者级数估计等非参数方法逼近φit，得到，将带入式（4）并对该式进行最小二乘回归得到β的估计值； （2）考虑企业的生存概率。使用Probit模型估计Pit得到；（3）估计资本系数和劳动系数。对于给定的初值α和γ，有，将对和进行非参数回归可以得到，基于矩条件E（ξitCapitalit）＝E（ξitAgeit）＝0对式 （5） 进行GMM估计即可得到α和γ的估计值。至此，OP模型中的所有参数已全部估计，进而可以测算企业TFP。

1.4.2 基于OP模型的改进模型

Levinsohn和Petrin（2003）指出企业存在调整成本，因此很多企业投资为零，使用OP模型测算企业TFP要求将投资为零的样本全部剔除，会造成很大损失［17］。LP模型选择将中间投入 （原材料）Mit作为生产率的代理变量，认为此时样本量损失较少，能够较好地解决内生性问题，获得投入要素的一致有效性估计。由于E（ξitMit）＝0的矩条件不再成立，此时OP模型的参数估计方法不再适用于LP模型。LP模型首先基于lnYit-E（lnYit｜lnKit，lnMit）＝β［lnLit-E（lnLit｜lnKit，lnMit）］+εit估计出非状态变量对应的参数β，其次基于矩条件E（ξit，Kit）＝E（ξitMi，t-1）＝ 0， 对Kit和Mit对应的参数指定初值，迭代得到最终的参数估计值。可以发现，LP方法没有考虑企业的退出问题。

Ackerberg等 （2006）指出，OP模型和 LP模型均认为劳动要素是自由变量，可以随时调整，但事实上企业劳动调整成本很高，企业作为自由变量的假设过于严格［18］。ACF模型假设劳动要素为资本要素、投资、中间投入以及TFP的函数，即Lit＝f［ωit（Iit，Kit），Kit］ （OP），Lit＝f［ωit（Mit，Kit），Kit］（LP）。 此外， ACF 指出 LP 模型使用中间投入作为代理变量，在参数估计的第一步存在多重共线性问题，因此他们对LP模型进行改进，提出新的估计方法。由于ACF同样忽略了企业的退出问题，所以他们的估计方法也只有两步。ACF模型第一步不估计任何弹性参数，只用非参数方法逼近φ，以实现ωit与εit的分离，第二步根据ωit的一阶马尔科夫过程和上述要素投入顺序的设定，运用GMM方法同时估计各弹性系数，进而得到企业TFP。

OP模型、LP模型和ACF模型均采用多阶段GMM方法来估计参数，其参数的标准差和检验统计量通常需要通过Bookstrap方法来获得，这极大地增加了企业层面测算的计算量。此外，ACF在第一步避免估计参数将丧失获取参数识别信息的可能性。Wooldridge（2009）尝试将上述多阶段同步进行，使用系统GMM方法估计参数［19］。具体而言，Wooldridge保留了OP、LP和ACF方法将生产函数取对数，并将ωit反解为代理变量函数所得到的线性方程，同时基于ωit的一阶马尔科夫过程假设，引入新方程。新方程将ωit替换为ωi，t-1的高阶多项式和演化扰动，而高阶多项式中的ωi，t-1被反解为前一期代理变量的函数。Wooldridge将两个方程联立，选择企业投入决策变量做工具，使用GMM方法更有效的估计了生产函数的参数以及TFP。

与ACF模型不同，GNR模型从另外一个角度尝试解决LP模型的多重共线性问题［5］。GNR将企业成本最小化的一阶条件进行适当变换，推导出中间投入支出与名义总产值之比的对数为资本、劳动和中间投入的函数， 即 lneit＝g（Lit，Kit，Mit）-εit， 其中g（Lit，Kit，Mit）为对数中间投入的产出弹性。GNR的参数估计方法分为3步：（1）依据上式，使用非参数方法逼近eit和εit，得到；（2）依据，使用非线性最小二乘估计得到与中间投入有关的参数θ1； （3） 令θ2表示其他剩余待估参数的集合，将基于θ2的 TFP表达式ωit（θ2）对ωi，t-1（θ2）进行回归， 得到的残差项记为εit（θ2）， 在E（εitLit）＝E（εitKit）＝ 0 的矩条件下， 估计出θ2。至此，GNR估计出所有的参数，在此基础上可以进一步测算企业TFP。

Klette和Griliches（1996）认为在不完全竞争市场中，企业产品价格与要素投入相关，将导致生产要素参数估计的产品价格遗漏偏误［20］。如果用行业产品价格指数对企业销售额进行平减得到的值Zit作为企业的产出，则Zit与生产要素之间的实际关系应为 lnZit＝αlnKit+βlnLit+ϑlnMit+（pit-）+ωit+εit，其中Mit为企业i在t时期的中间投入，pit为企业i在t时期的产品价格，为t时期的行业产品价格。De Loecker（2011）使用有条件的需求系统，给出企业生产单一产品的需求函数，改进LP模型，尝试解决不完全竞争市场中的产品价格遗漏偏误［21］。经过合理变换，De Loecker得到不完全竞争市场中的对数化生产函数表达式：，其中Qt为行业时期t的产品需求，与不可观测的需求冲击成比例，与产出价格相关。通过上式可控制遗漏产品价格，测算得到，又，可以最终得到企业TFP，其中δ为行业内不同产品需求的替代弹性。

De Loecker考虑的是单一产品企业，当涉及多产品企业时，不同种类产品的需求将导致多产品的产出结构内生性问题。Beveren（2012）假设行业内的企业共生产N种产品，把行业细分为N个次级部门，次级部门有不同的需求价格弹性（次级部门的产品需求替代弹性）δs，此时生产函数为，其中s为次级部门，N为次级部门总量，Iis为虚拟变量，如果企业i有次级部门s，Iis＝1， 否则Iis＝0； lnQts用不同次级部门的产出衡量，表示行业内不同次级部门的需求变动，表示行业产出［2］。 基于上式估计出， 由， 可以得到企业TFP。

上面本文讨论的各种结构模型方法均假设企业TFP服从外生的一阶马尔科夫过程，但事实上企业的很多行为都会直接或间接的影响到自身TFP，如技术升级、出口参与、R＆D投入等，此时企业要素投入与随机生产率冲击ξit＝ωit-E（ωit｜ωi，t-1）相关，原始的矩条件不再成立，这将导致生产函数的参数估计出现偏误。因此很多学者在企业TFP测算过程中考虑生产率演变的内生性。Van Biesebroeck（2005）将企业滞后一期的出口状态引入到生产率的演变过程中［22］；Doraszelski和Jaumandreu（2013）将企业滞后一期的 R＆D投入引入到生产率的演变过程中［23］。具体而言，内生生产率过程假定企业TFP服从以下的一阶马尔科夫过程：ωit＝E（ωit｜ωi，t-1，Wit）+ξit。 其中Wit为直接影响企业未来TFP的某种企业行为或某几种企业行为的集合。此时ξit与生产要素不相关，矩条件成立，可以使用GMM方法估计出生产函数的参数，进而测算企业TFP。

2 基于“生产前沿面”思想的测算方法

在Solow基于余值思想测算TFP的同时，Far-rell（1957）提出基于生产前沿面和合适的距离函数，衡量微观厂商的投入产出效率［24］。生产前沿面是经济学中生产函数向多产出情况的一种推广，更贴合微观企业多投入和多产出的实际。位于生产前沿面上的投入产出组合是技术上最有效率的，即获得给定产出至少需要生产前沿面对应的投入水平，或者给定投入至多可以达到生产前沿面对应的产出水平。偏离生产前沿面的投入产出组合通常被认为是技术无效的，距离生产前沿面越远的组合，其相对的技术效率越低。基于Farrell的思想，学术界主要演变出两类模型以评价生产单元的技术相对性，分别是数据包络分析方法和随机前沿分析方法。近年来，学者们尝试使用这两种方法测算企业TFP，并引入Malmquist指数，将DEA、SFA分别与Malmquist指数结合，测算企业TFP增长率，并将增长率进一步细化分解。

2.1 数据包络分析法

数据包络分析是数学、运筹学、数理经济学和管理学科的交叉领域，使用数学规划方法测算评价具有多种投入和产出的决策单元 （Decision Making Unit，DMU）的相对有效性。其本质是基于各DMU的观察数据，以最小投入或最大产出为目标，以生产可能集为约束，通过多目标规划，得到DMU投入数据和产出数据包络面的有效部分，构建投入导向或产出导向的确定性生产前沿面。之后通过距离函数判断各DMU是否偏离生产前沿面以及偏离程度，偏离越远，DMU的相对有效性越低。

DEA方法通常将企业TFP定义为其加权产出与加权投入之比，同时将该比值作为各企业与生产前沿面的距离。具体而言，对于某一确定企业，其产出和投入权重是在样本内所有其他企业使用同样权重计算得到的TFP不大于1的条件下，使得该企业产出投入比最大化的权重。可以发现，DEA方法实质上是将每个企业投入产出的线性组合比和其他企业相应的投入产出比进行比较，得到企业TFP的相对值，此时企业TFP不超过1，数值越大，意味着企业的相对有效性越高。

Charnes等 （1978）假定生产单元规模收益不变，最早提出了CCR数据包络模型［25］。Banker等 （1984）对CCR模型进行改进，假设生产单元规模收益可变，提出了BCC数据包络分析方法，此时测算得到的企业生产效率可以进一步分解为纯技术效率和规模效率［26］。CCR模型和BCC模型是研究者最常使用的两种测算企业相对效率的数据包络模型，在使用时，既可以选择投入导向的相对效率测度模型，也可以选择产出导向的相对效率测度模型。此外，学者们近年来考虑不同的生产可能集、距离函数、选择偏好以及变量类型等，提出很多新的数据包络模型。这些模型关于数据包络的基本思想保持不变，不同模型会选择不同的生产前沿面和距离函数，篇幅所限，在此将不一一赘述。

2.2 随机前沿分析法

Meeusen 和 Broeck（1977）以及 Aigner等（1977）分别在各自的文章中提出随机前沿分析方法［27，28］，该方法的一般形式如下所示：

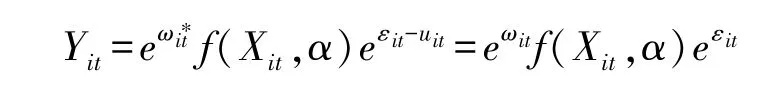
其中eεit-uit为复合结构的误差项，εit服从对称的独立同分布，衡量各种随机因素对于前沿产出的影响；uit服从单边的独立同分布，衡量技术上的非有效程度；ωit＝ω∗it+uit为企业i在t时期的TFP。

SFA可以看作是通常的生产函数与前沿面思想的结合，它在考虑随机因素对产出造成干扰的同时，将生产单元的非效率项e-uit从测量误差中分离出来，并将其作为衡量投入产出组合偏离前沿面程度的距离函数。此外，SFA依据生产函数的数理表达式确定生产前沿面，同时随机误差项eεit的存在使得生产前沿面具有随机性，与DEA的确定性生产前沿面相比更符合实际。

在测算时，通常假设εit与uit相互独立，εit服从正态分布，uit可服从指数分布，截断正态分布或 Gamma分布， 实证中最常用的是截断正态分布。对于截面数据，通常使用极大似然方法或矩方法来估计参数；对于面板数据，当模型为固定效应模型时，通常使用极大似然方法或者虚拟变量最小二乘方法来估计参数，当模型为随机效应模型时，通常使用最大似然方法或者可行广义最小二乘方法来估计参数。

同之前 “余值”法测算企业TFP及其增长率相似，在估算出模型中各参数之后，可以得到企业TFP，区别在于此时可以从TFP中区分出技术效率项e-uit。e-uit＝1意味着企业的投入产出组合在生产前沿面上，企业技术有效；e-uit＜1意味着企业的投入产出组合偏离生产前沿面，企业技术无效，依据e-uit的值可以明确企业具体的技术无效程度。此外，对企业TFP增长率进行分解可得：

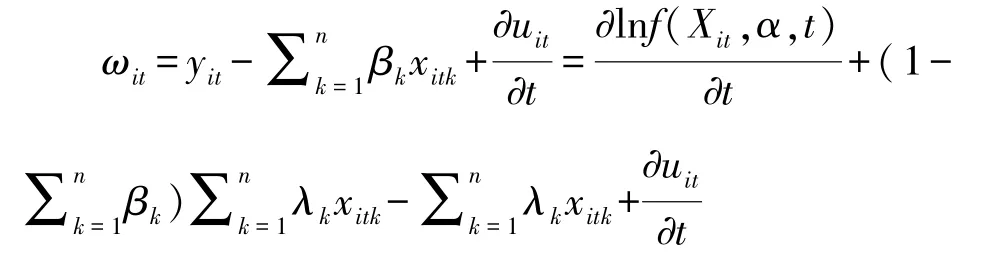
意味着此时影响企业TFP变化的因素除了技术进步率、规模收益变动率以及资源配置效率变化率之外，还有企业的技术效率变化率。

2.3 基于“前沿面”思想的企业TFP增长率测算方法综述

Caves等 （1982）基于Shepherd距离函数构建了Malmquist生产率变化指数，在实证研究中，通常以距离函数为枢纽，将DEA或SFA与Malmquist指数相结合，考虑企业生产过程中的技术非效率，测算其 TFP 变化率［29］。

在测算时，既可以基于投入导向的生产前沿面构建Malmquist指数，也可以基于产出导向的生产前沿面构建Malmquist指数。样本点基本不会出现在投入导向前沿面的左侧或下方，也不会出现在产出导向前沿面的右侧或上方。实际中，企业更倾向于考虑扩大产出，因此通常基于产出导向的生产前沿面构建Malmquist指数。

令Xit＝ （xi，1t，xi，2t，…，xi，nt）′，Yit＝ （yi，1t，yi，2t，…，yi，mt）′分别表示企业i在时期t的投入向量和产出向量，dt（Xit，Yit）为衡量企业i在时期t的投入产出组合偏离时期t生产前沿面程度的距离函数。则企业i以t和t+1时期的技术水平为参照，以时期t投入组合为基准的Malmquist指数分别为mt＝。为了避免基准选择的任意性，Fare等 （1994）将产出导向的Malmquist指数定义为上述两者的几何平均值， 即［30］：

在企业规模收益不变的假设下，可以将TFP变化分解为技术变化以及技术效率变化，即：

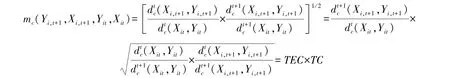
基于上式，此时如果进一步考虑企业规模收益可变，可以将企业的技术效率变化分解为规模效率变化和纯技术效率变化，即：分别为企业i由时期t到t+1的技术变化，纯技术效率变化以及规模效率变化。

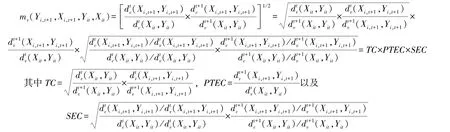
Malmquist指数大于1、小于1和等于1分别意味着企业i由时期t到t+1的TFP水平分别是增加、下降和无变化的，再进一步比较TC、PTEC和SEC与1的大小关系，便可明确企业TFP变动的具体原因。

3 结 语

本文区分TFP和TFP增长率两个概念，对企业TFP及其增长率的测算方法进行系统梳理。“余值”思想以及 “生产前沿面”思想是学术界测算TFP及其增长率的两种主流思想。一直以来，学者们都尝试从不同角度改进方法，得到更好的测算结果。基于 “余值”思想的测算方法聚焦于改进最小二乘估计以克服由于内生性、样本选择偏误、价格指数影响效应、多产品与单一产品等因素导致的估计偏差：工具变量法、固定效应模型和动态面板模型通过寻找工具变量或者对扰动项做出严格的先验设定以解决内生性问题，缺陷在于忽略了数据背后的企业行为；结构模型进一步尝试利用企业的行为和决策信息，实现经济理论和计量方法的统一，更好地解决最小二乘估计面临的系列问题。基于 “生产前沿面”思想的测算方法则聚焦于修正生产前沿面和距离函数以研究指定企业的TFP相对于样本中其他企业TFP的表现。

通过本文的梳理，相关研究者对微观企业TFP的测算方法在理论上有比较全面透彻的了解，进而在实证分析中可以依据研究目的和数据特征选择合适方法。但需要指出的是，即使针对同样的样本和变量，不同方法得到的结果可能也会差异较大，背后的具体原因有待进一步深究。建议实证测算企业TFP时可以适当选取多种方法，保障结果的稳健性。