分体式消隙蜗杆副安装误差对接触强度的影响

何亚银， 梁智鸿， 高卫丽

(1.陕西理工大学 机械工程学院，陕西 汉中 723000；2.陕西省工业自动化重点实验室，陕西 汉中 723000)

消隙蜗杆副具有传动平稳、振动冲击和噪声小、传动比大和消除反向间隙等优点，被广泛应用于国防、冶金、造船和化工等行业。作为一种新型的消隙蜗杆副，分体式消隙蜗杆副采用两段相同螺旋升角的蜗杆[1]，通过旋转调节两段蜗杆之间的距离来消除蜗杆反向间隙，由于两段蜗杆在轴截面上的齿形为瘦长齿，有较大的齿顶高系数和顶隙系数，工作压力角比普通蜗杆的压力角小，具有较小的导程角等特点。由于该蜗杆副的结构特点，在使用和安装时较普通的蜗轮蜗杆更容易出现安装误差，使得变形过大或应力过大而影响蜗杆副结构的传动精度，所以对其安装精度要求更高。因此，通过研究分体式消隙蜗杆副安装误差对接触强度的影响，获得许用的角度安装误差范围具有非常重要的工程意义。

Gonzalez-Perez等在文献[2]中提出了一种基于赫兹理论的局部轴承接触齿轮传动应力分析方法，根据接触面积、最大接触压力、压力分布、最大特雷斯卡应力和特雷斯卡应力分布，建立并验证了有限元模型，该模型的验证适用于赫兹理论。Gonzalez-Perez等在文献[3]中提出的有限元模型允许对整个网格周期进行分析，并且基于网格细化的多点约束的应用和具有减少的积分点的元素的应用，获得关于接触应力和弯曲应力的精确结果。马玉娟等[4]分析了不同类型的蜗杆之间承载能力以及变形间的关系，利用有限元法，建立蜗杆副的动力学分析模型，在啮合瞬间进行瞬态动力学分析，研究结论为ZC1型蜗杆在减速器等领域中的应用提供理论依据和工程应用价值。Falah等[5-6]预测了啮合周期内装配误差对单包络(圆柱)蜗杆传动局部接触应力分布的影响，用切片法估算单包络(圆柱)蜗轮传动的载荷份额和计算瞬时齿啮合刚度和应力，得出了有装配误差的加载齿轮的控制因素是啮合刚度和误差量、误差量与相邻齿对之间的载荷分担有关的结论。ZHU Xi-jun等[7]基于啮合理论推导了变齿厚平面蜗杆传动的齿面方程，建立了齿隙可调变齿厚面包络蜗杆的有限元分析模型，并对齿隙可调变齿厚平面包络蜗杆传动进行了有限元分析，得出了蜗杆传动的主应力分布和齿间载荷分布的规律。上述文献采用不同的理论和不同的有限元接触方法分析了不同蜗杆副的强度和稳定特性，考虑了传动误差和装配误差对齿轮局部齿面接触的影响，也考虑了齿隙可调蜗杆的弯曲应力，但没有关于分体式蜗杆的强度特性的分析和关于角度安装误差对齿轮局部齿面的接触应力和变形的分析。

本文以分体式消隙蜗杆副为研究对象，采用数值分析法与有限元分析法相结合的方法，以获得满足分体式消隙蜗杆副装置使用要求的许用角度安装误差范围。

1 蜗轮蜗杆接触强度的数学模型

几何结构、工况、齿面摩擦和材料等都会对蜗轮蜗杆的接触强度产生影响，蜗轮蜗杆接触并受压力作用时，接触面为一狭长矩形，在接触面上产生接触应力，并且最大接触应力位于接触区中线上，为了分析蜗轮的接触强度，以德国物理学家海因里希·鲁道夫·赫兹于1882年提出的赫兹公式[8]为前提，并结合蜗轮蜗杆接触线啮合的条件得到：

(1)

式中σH为齿面接触应力(MPa)；ZE为材料弹性系数，铸锡磷青铜蜗轮和钢蜗杆相配为160 MPa1/2，与蜗轮和蜗杆材料的泊松比和弹性模量相关；K为载荷系数[9]；Fn为法向力(N)；L0为最小接触线长度(mm)；ρ∑为综合曲率半径(mm)。

赫兹公式解析：

(2)

式中T2为蜗轮扭矩(N·mm)，d2为蜗轮分度圆直径(mm)，α为蜗轮在分度圆上的压力角(度)，γ为蜗杆在分度圆上的导程角(度)。

蜗轮齿沿齿宽方向成弧形包在蜗杆上的接触线长度，如图1所示。最小接触线长度计算公式为

(3)

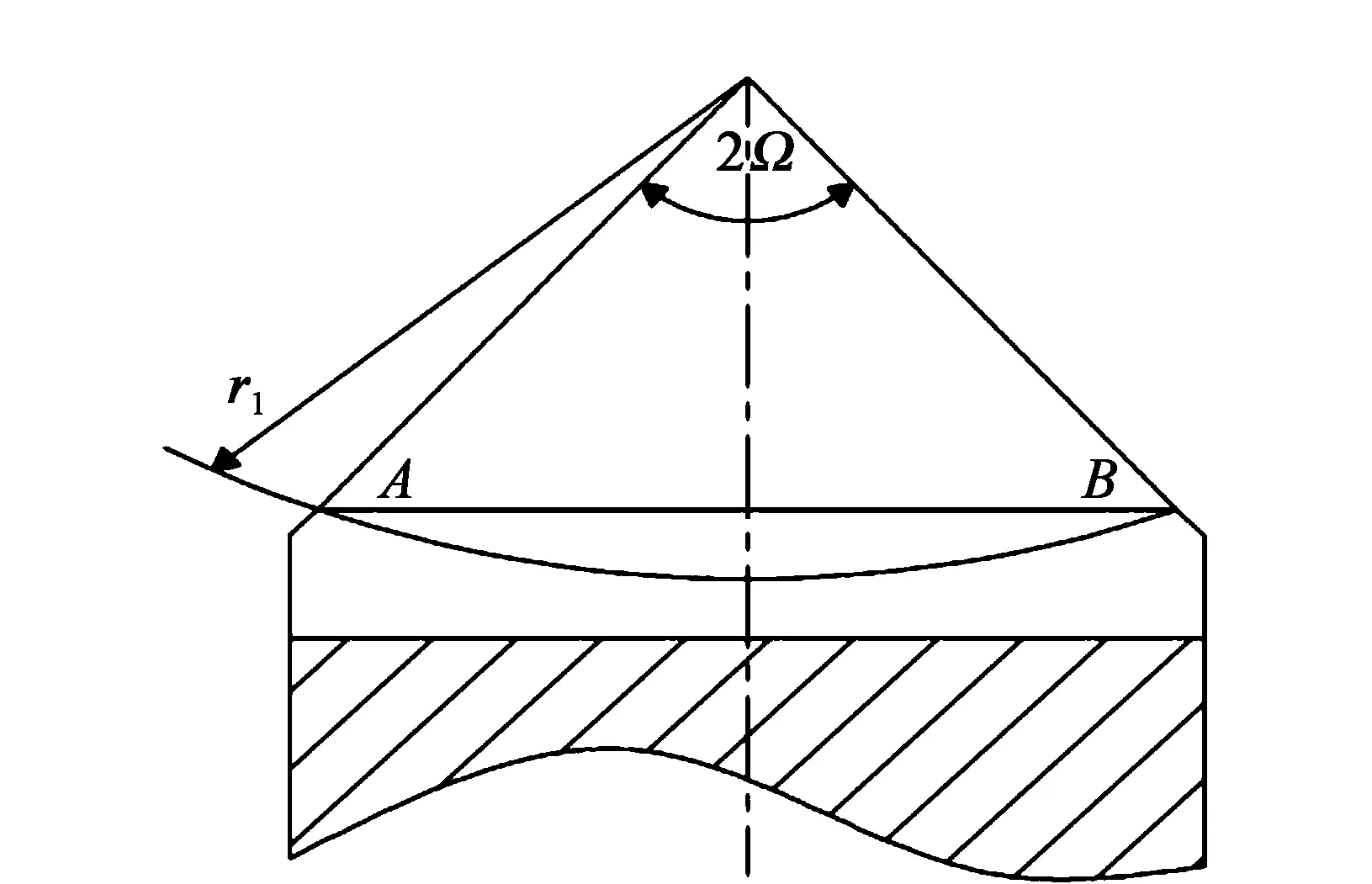
图1 接触线长度

由于渐开线圆柱蜗轮蜗杆的啮合传动过程与齿轮齿条的啮合传动过程相似，为了简化计算，假设蜗轮齿面在计算点处的曲率半径ρ1=+∞以及sinαn=sinαcosγ。通过几何关系得到如下公式：

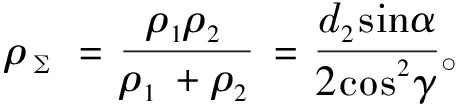
(4)

把式(2)—(4)代入式(1)并整理，得到蜗轮在接触线处的接触应力为

(5)

2 分体式消隙蜗杆副建模

2.1 分体式消隙蜗杆副的结构特点

图2为分体式消隙蜗杆副传动原理图，蜗杆由蜗杆轴和蜗杆套组成。在接触部位，蜗杆轴的右齿面与蜗轮的左齿面接触，蜗杆套的左齿面与蜗轮的右齿面接触。

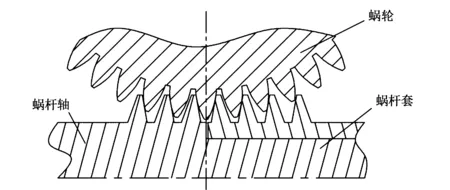
图2 分体式消隙蜗杆副传动原理图

蜗杆轴和蜗杆套在轴向截面上的齿廓曲线为直线，端面为阿基米德螺旋线。蜗杆两侧压力角不相等，分体式蜗杆的蜗杆轴和蜗杆套只有压力角较小的一侧与蜗轮啮合，故蜗杆两侧的压力角相等且等于较小压力角。

2.2 三维实体建模

表1列出了本文采用的分体式消隙蜗杆副的蜗轮蜗杆的基本参数[12]。

表1 蜗轮蜗杆基本参数

图3 蜗杆副实体模型

基于啮合理论得到蜗杆齿廓的数学模型，运用三维建模软件UG参数化建模功能模块，建立精确的齿槽形状和蜗杆螺旋线，进行布尔减运算完成蜗轮蜗杆的实体建模，最后利用虚拟装配得到蜗杆副实体模型，如图3所示。

3 分体式消隙蜗杆副有限元分析

3.1 前处理与边界条件

蜗杆副的材料主要从弹性模量、泊松比和密度3个方面定义，具体属性见表2所示。

表2 蜗杆副材料属性

利用ANSYS生成有限元接触模型[13]，设置蜗杆轴、蜗杆套和蜗轮的elementsize(网格尺寸)为1 mm，局部齿接触面做细化处理及对网格弯曲区域进行细化处理，最后得到699 658个单元，410 386个节点。接触方式为面-面有摩擦接触[14-15]，接触类型选择性刚性-柔性的接触。

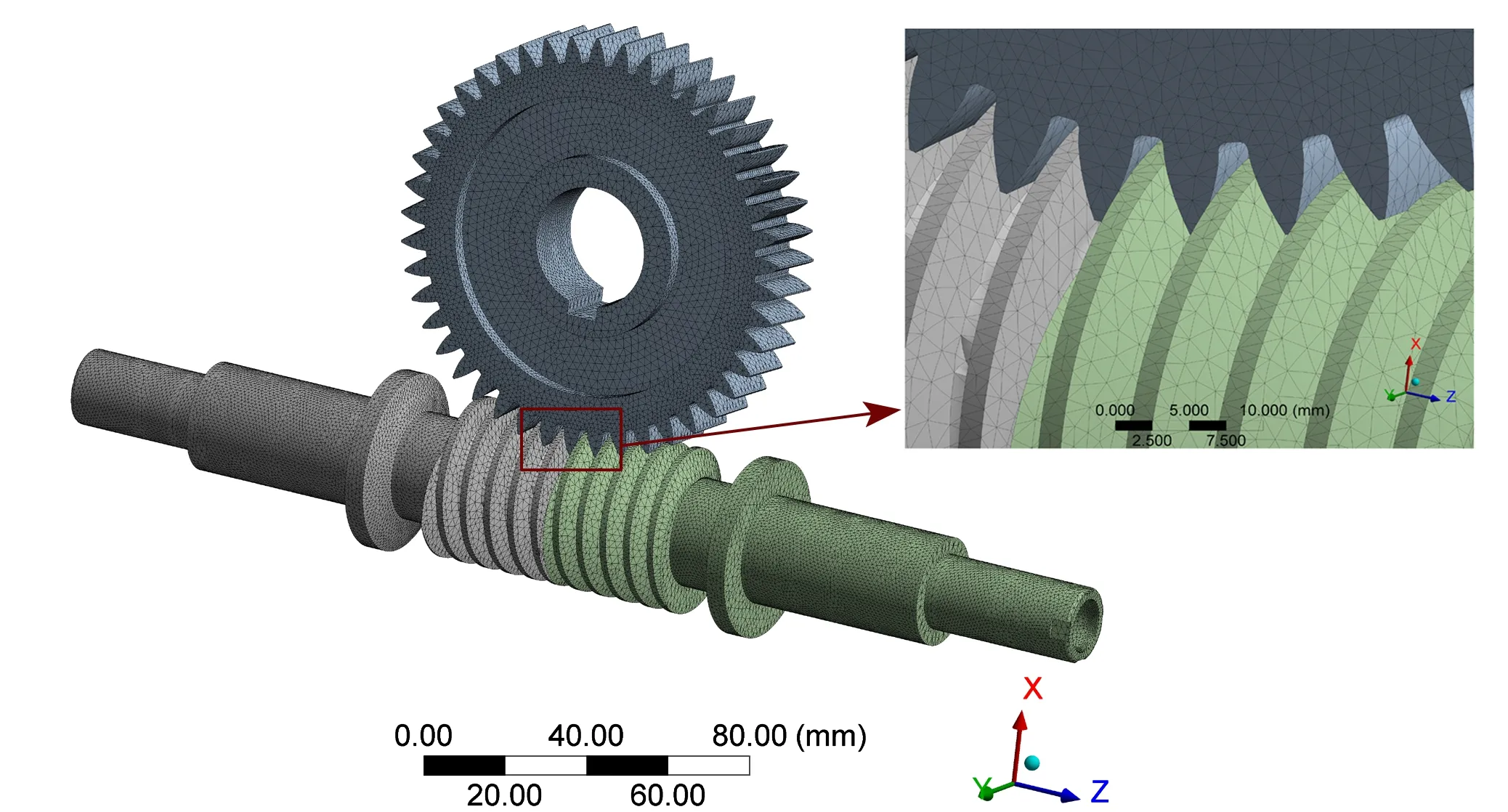
图4 蜗杆副有限元模型

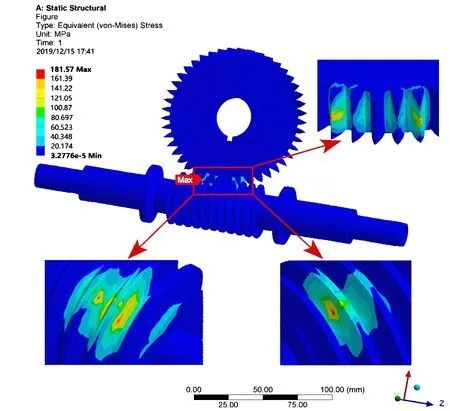
图5 蜗杆正转有限元模型应力图

定义载荷与约束：(1)限制蜗轮内圈的X、Y、Z方向上的移动自由度，不限制蜗轮内圈绕自身轴线的转动自由度；(2)限制蜗杆轴与蜗杆套内圈的X、Y、Z方向上的移动自由度，不限制蜗杆轴与蜗杆套的切向自由度；(3)将蜗杆副传递的转矩换算成扭矩载荷施加在蜗杆轴两端，总载荷为T1。所生成的蜗杆副有限元模型如图4所示。

3.2 有限元分析

设定边界条件时，将蜗杆设置为主动件且主动力由蜗杆轴传入蜗杆副，定义蜗轮的负载扭矩为T2=50 000 N·mm，蜗轮蜗杆的传动效率为η=0.7，传动比为i=45，则蜗杆的扭矩为T1=T2/(iη)=1587 N·mm。根据接触应力理论，将T2、表1和表2中的数据代入公式(5)得蜗轮的接触应力为σH2=192.71 MPa。

定义蜗杆螺旋方向为正方向，在不考虑安装误差的情况下，分别给蜗杆正向与反向施加载荷作有限元计算，当正向施加载荷，即扭矩为T1= 1587 N·mm时，所得的应力图和变形图如图5和图6所示。从图中可以看出蜗杆副的最大应力在蜗轮上，这与理论分析情况相符，从有限元计算结果得到额定载荷为正向和反向时最大接触应力分别为181.57 MPa和184.13 MPa，比理论计算结果稍小且误差分别为5.78%和4.45%，证明了该分体式消隙蜗杆副建模方法的正确性。

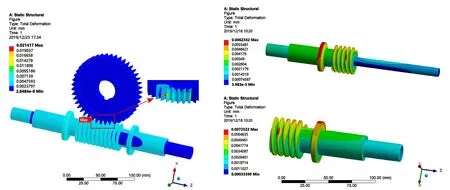
(a)蜗杆副及局部放大图 (b)蜗杆轴与蜗杆套

3.3 安装误差对接触强度的影响

对于主动件蜗杆正向旋转和反向旋转时，对蜗杆轴与蜗杆套存在0°、0.2°、0.4°、0.6°、0.8°、1°的安装误差的情况下进行有限元分析，计算得到蜗杆不同转向不同安装误差下蜗杆副的最大接触应力和最大变形量如表3和表4所示。

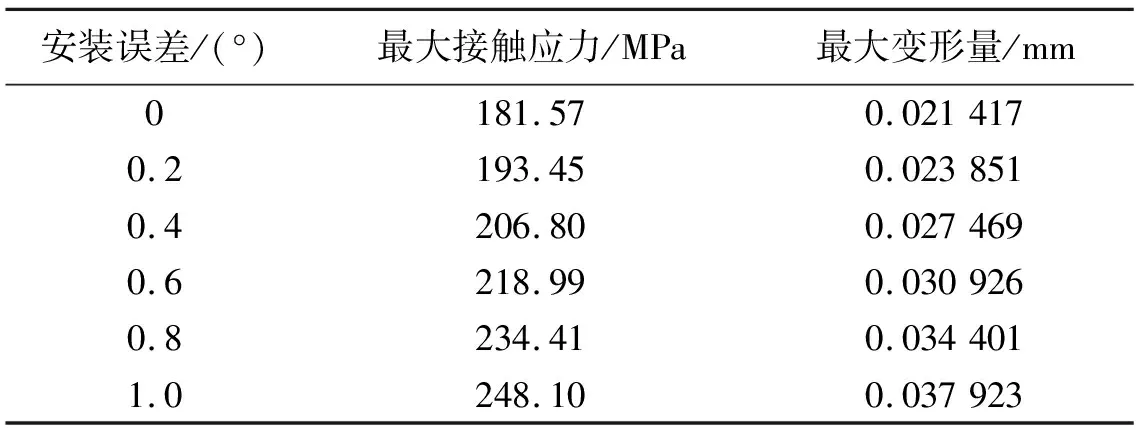
表3 蜗杆正转时蜗杆副的最大接触应力和最大变形量

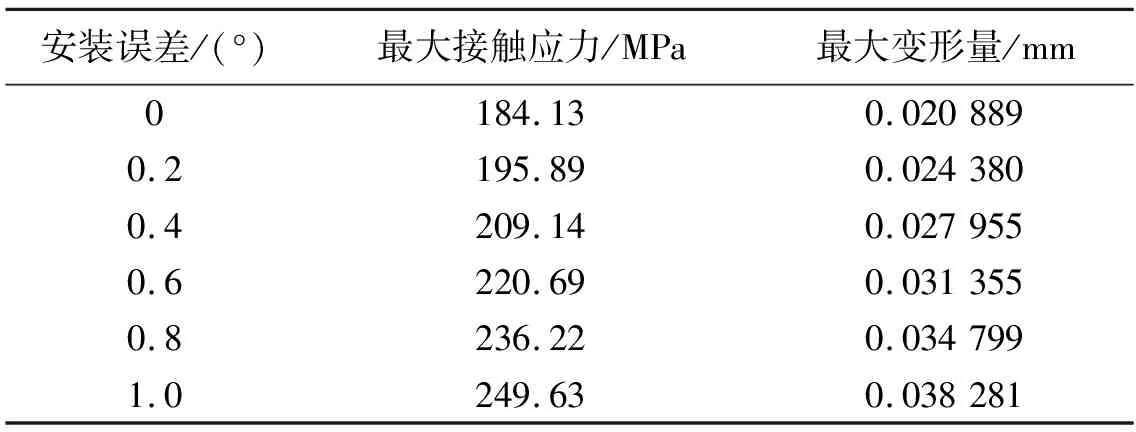
表4 蜗杆反转时蜗杆副的最大接触应力和最大变形量

根据已知数据基于MATLAB软件用最小二乘函数拟合方法拟合数据曲线公式。

当蜗杆正向旋转时，得最大接触应力(y1)与安装误差(x)关系的曲线公式为

y1=7.736 6x2+59.080 5x+181.509 6，

(6)

最大变形量(y2)与安装误差(x)关系的曲线公式为

y2=-0.006x3+0.011 1x2+0.011 4x+0.021 4；

(7)

当蜗杆反向旋转时，得最大接触应力(y3)与安装误差(x)关系的曲线公式为

y3=7.754 5x2+57.965 5x+184.123 9，

(8)

最大变形量(y4)与安装误差(x)关系的曲线公式为

y4=0.000 5x3-0.001x2+0.017 9x+0.020 9。

(9)

数据拟合曲线如图7和图8所示。

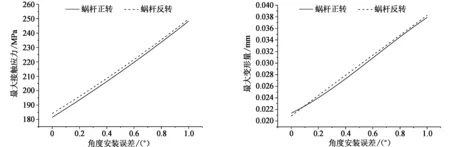
图7 最大接触应力与安装误差关系曲线 图8 最大变形量与安装误差关系曲线

所研究的蜗轮材料的许用应力为220 MPa，代入公式(6)和公式(8)分别得蜗杆正向旋转时安装误差为x1=0.604°和蜗杆反向旋转时安装误差为x2=0.575°。

由图7和图8可以看出蜗杆副的最大接触应力与安装误差成正相关，其中在同一角度安装误差，蜗杆反转时的最大接触应力比蜗杆正转时的接触应力大；蜗杆反转时最大齿面接触应力随角度安装误差变化幅度相对蜗杆正转小；蜗杆副的最大变形量与安装误差也成正相关，区别点是在角度安装误差小于0.1°时，蜗杆反转的蜗杆副最大变形量小于蜗杆正转的最大变形量，角度安装误差大于0.1°时，则情况相反，并且蜗杆反转时蜗杆副的最大变形量与角度安装误差的正相关关系更稳定。

4 结论

对有限元分析结果数据进行处理，并且根据数据绘制表格和拟合曲线，可得到以下结论：

(1)将传统蜗杆副强度计算的经验公式结果与有限元强度计算结果对比，得出经验公式计算结果大于有限元计算结果，可以看出解析法并不能准确的体现分体式消隙蜗杆副的强度性能，具有一定的误差；接触应力结果误差小于6%，说明了这种建模方法的正确性，为分体式消隙蜗杆副的建模和强度分析提供了理论依据。

(2)分体式消隙蜗杆副的最大接触应力与安装误差成正相关，在同一角度安装误差下，蜗杆反转与蜗杆正转相比较，蜗杆反转的最大接触应力较大，蜗杆正转的最大接触应力较小；在不同的角度安装误差下，蜗杆反转时比蜗杆正转时最大齿面接触应力随角度安装误差变化幅度小；根据标准蜗轮材料的许用应力，结合有限元法分析结果可知安装应小于0.55°，即对比于分体式消隙蜗杆副的蜗杆螺旋角，角度安装误差应不超过16%。此结论为分体式消隙蜗杆副的工程安装提供了相应的理论依据。

(3)分体式消隙蜗杆副的最大变形量与安装误差成正相关，当角度安装误差小于0.1°时，蜗杆反转时的蜗杆副的最大变形量小于蜗杆正转时的最大变形量；当角度安装误差大于0.1°时，则情况相反，并且随着角度安装误差的增大，蜗杆反转时蜗杆副的最大变形量与角度安装误差的正相关关系更稳定。