基于自然进化策略的多工艺融合结构件加工变形控制方法*

刘醒彦，刘长青

（南京航空航天大学机电学院，南京210016）

加工变形是航空大型整体构件（特别是薄壁零件）数控加工中常见的问题，加工变形导致零件几何误差和尺寸公差超差[1]。波音公司的一项研究表明，由于零件加工变形引起的工件报废损失超过29 亿美元[2]。影响加工变形的因素有很多[3-4]，包括毛坯料的初始残余应力、零件尺寸结构、刀具参数、加工工艺等，其中初始应力引起的变形占部件总变形量的90%以上[5]。

残余应力与加工变形的相关研究表明，加工变形是材料残余应力、零件的尺寸外形以及零件在毛坯中的位置关系的函数[6]。数控加工过程中，大量的材料被去除，毛坯内部残余应力平衡被打破，形成力矩导致工件变形，其中力矩受工件几何和残余应力共同影响。对毛坯施加预变形，改变毛坯内部的初始应力场分布，最终影响工件上应力分布，从而影响工件最终变形。毛坯中的应力分布在整个材料中，工件只是毛坯的一部分，改变工件在毛坯中位置会影响工件最终内部应力分布，同样影响工件最终变形。工件变形是工件几何和残余应力共同作用的复杂过程，在工件几何确定的情况下，很难通过单一变量寻找到合适的工件应力分布抑制工件变形。因此综合考虑预应力与加工位置的加工变形控制方法，对毛坯施加力载荷，使毛坯初始残余应力分布发生变化，选择适当的加工位置，使工件在预变形毛坯获得力矩较小的应力分布。此外，由于调节预应力、工件加工位置与加工变形的关系极其复杂，参数求解空间巨大（假设加工底面可施力点离散为j 个，在n 个点施加力，力的取值离散为m 个数值，加工位置离散为k 个，则解空间为k·mn·Cjn）。自然进化策略是近期在求解黑盒优化问题上有着良好应用的一类算法[7]，且其中的PEPG 算法[8]在强化学习的模型参数搜索上相比其他算法有着亮眼的表现。因此，文本拟采用PEPG 搜索最优参数，使工件最终加工变形被抑制。

加工变形是造成飞机结构件加工质量问题的主要原因之一，所以加工变形控制也成为飞机结构件质量提升的重要方法。为了控制减小航空结构件的变形，提高结构件的加工质量，国内外的学者做了大量的相关研究。根据加工过程的阶段不同，加工变形控制措施主要有：加工之前的变形预控制、加工过程中的变形控制。

（1）变形预控制。加工之前的加工变形控制主要通过优化材料特性，降低材料中的初始残余应力。Zhang等[9]采用机械拉伸降低毛坯初始残余应力，当拉伸比达到1.5%～3%时，残余应力的大小可以降低70%～80%。Younger 等[10]的相关研究发现，增加人工时效时间可以减小50%的毛皮初始残余应力。上述方法有效地降低了材料的应力水平，有力地降低了工件加工变形，但不能彻底消除应力，在加工过程中零件依然会随着材料被去除而发生变形。

（2）加工过程中的变形控制。优化材料特性能够降低材料中初始应力，但是无法消除应力。加工过程中，毛坯内部大量材料被去除（高达90%以上），同时切削过程中产生切削应力和热应力，应力耦合下加剧了内部应力的不平衡。因此加工过程中的变形控制有着重要的意义。

加工过程中的变形控制主要通过优化加工工艺。Fuh 等[11]提出了一个铣削铝2014-T6 材料的残余应力预测模型来优化零件变形，这个数学模型参数包括切削速度、进给量、切削深度、刀具几何形状、刀具圆角半径和磨损等。Umbrello 等[12]研究了材料、刀具几何形状和加工参数对残余应力的影响，并基于有限元和切削试验的方法，提出了基于神经网络的切削残余应力的预测模型改善加工质量。Sasahara 等[13]利用仿真计算的方法研究了多种加工顺序对零件加工中残余应力分布的影响，得到最优的加工顺序。Cerutti 等[14]研究了加工过程中工件刚度对变形的影响，通过仿真分析，建立了刚度与零件变形的模型，同时利用仿真软件研究了加工顺序对零件变形的影响。Outeiro 等[15]基于仿真手段研究了特定工件在不同的加工顺序下的残余应力场分布情况，进而根据研究内容提出了加工顺序优化方法。Sasahara 等[13]针对薄壁结构件，基于遗传算法优化了零件的加工顺序，减小了零件的变形。Ye 等[16]为了主动控制轴承零件的残余应力状态，提高轴承零件的疲劳寿命和加工质量，采用了一种新的预应力硬切削方法。He 等[17]通过正交试验研究了加工参数和预应力对40Cr 钢残余应力的影响，结果表明预应力能有效提高残余压应力，对加工质量有明显影响。何志英[18]、Cerutti[14]和Brinksmeier 等[6]的研究表明，工件在毛坯不同位置加工变形不同。Nervi[19]以弹性理论为基础，建立了预测加工变形的理想数学模型，采用铝合金预拉伸板7050-T7451 作为研究对象，设计“Z 形零件”来研究零件在毛坯中的位置对加工变形的影响，研究结果表明试样位置对加工变形有较大的影响。张峥[20]通过数值分析和试验确定余量分配方式对加工变形的影响，以T 型截面的缩比试样进行变形和预测分析。

上述方法都实现了加工变形的抑制，同时研究表明对毛坯施加预变形，改变加工位置能影响工件加工变形。但是工件变形是工件几何和残余应力共同影响的复杂过程，单一地调整毛坯预变形、加工位置等因素很难达到对加工变形控制的效果。对毛坯施加预变形，构建一个新的应力环境，但是无法确定在此应力环境下的最优区域。调整零件余量分配的变形控制，都是在给定毛坯应力水平下控制加工变形，无法构造更优的毛坯应力分布，优化的空间具有下限。因此本文将综合考虑毛坯预变形和加工位置作为控制条件，以最小化加工为目标，采用PEPG 优化算法寻找最优参数。

1 多工艺融合的加工变形控制方法

针对加工变形控制问题，本文提出基于自然进化策略的多工艺融合结构件加工变形控制方法，以使毛坯预变形的力载荷与加工位置同时作为工艺变量，控制加工变形。

数控加工过程中，大量的材料被去除，工件内部应力不平衡，形成力矩导致工件变形，如式（1）所示。

在装夹时，通过对毛坯施加力载荷f，使毛坯在加工前产生预应力σ*，产生的预应力与毛坯初始残余应力叠加，形成新的应力场σ。

其中，xi为施力点到约束点的距离；d 是厚度方向到中层性的距离；i，j 为x，y 方向；I 为惯性积。

通过对毛坯施加位移约束后，毛坯内部形成新的应力场，在此应力场确定加工位置z 后，工件内部应力σi（z）受加工位置影响，工件加工后形成力矩。

根据当前几何和力矩可以得到变形D 和力矩M 的关系。

其中，H 为与工件几何相关。式（5）说明加工变形与毛坯预变形以及加工位置之间关系。因此，以最小变形作为优化目标，采用自然进化策略寻找最优工艺参数，可抑制工件变形。

2 基于自然进化策略的多工艺参数优化

根据式（5），毛坯力载荷f 和加工位置z 对加工变形有着重要影响。由于毛坯力载荷、加工位置与最终工件变形的关系复杂，很难获得精准的函数关系。所有通过调整力载荷f 和加工位置z 获得当前工件最小加工变形，本质上是一个黑盒优化问题。通过力学模型建立参数优化模型，采用自然进化策略进行参数的优化计算，然后，选择一种零件验证优化后参数的效果。

2.1 优化变量

根据上述公式，毛坯的预应力受力载荷的数值和施加位置影响，此外工件在毛坯中的位置也影响着加工变形。因此力载荷的数值fi、施加位置（xi，yi）、加工位置Z都是优化模型的重要参数。其中，力载荷施加位置不能超出毛坯平面，工件加工位置不能超过工件厚度d，力载荷不能使毛坯发生塑性变形。因此，上述参数的约束范围如下：

其中，z 为工件顶面到毛坯底面的距离；F*为毛坯发生塑性变形的力；X1，X2，Y1，Y2为毛坯长宽边界。

2.2 优化目标

对工件最终变形来讲，上述变量是具有很大的求解空间的。只有极少的预变形形成的新应力场能够抑制变形，而且新应力场里只有少数区域下加工才能抑制变形。

本问题是寻找能够抑制加工变形的参数最优解。加工最终变形受力载荷F（x，y，f）和加工位置z 影响，因此以最小化最终加工变形为优化目标，获得参数优解。

2.3 PEPG优化算法

PEPG 是一种解决黑盒优化问题的优良算法，采用自然梯度在最大适应方向更新搜索分布的参数，从而实现优化。因此本文采用PEPG 实现优化上述参数的优化计算。

优化目的是最小化加工变形量，需要一个变形衡量指标，工件变形主要为沿厚度方向的弯扭变形，在长度方向变形可忽略，且工件变形后工件厚度的变化可以忽略，因而本文从加工后工件上顶面测量n 个点的厚度方向变形值。以n 个点变形的最大值与最小值之差t 作为变形衡量指标。

PEPG 算法的超参数确定是提高收敛速度和质量的重要保障，初始标准差σp=0.5，学习率r=0.01，种群数n=29。

2.4 有限元计算模型

针对上述问题的优化，需要一个求解环境。对毛坯施加位力载荷发生预变形，再按给定加工位置获得加工变形是一个复杂的力学求解问题。为优化计算提供力学求解平台，本文基于ABAQUS 有限元软件二次开发，建立有限元计算模型，如图1 所示。有限元建模过程：

（1）建立预变形模型Model–1，按层施加初始残余应力，按给定力载荷位置与数值对毛坯施加力载荷，运行模型并计算结果。

（2）建立加工变形计算模型Model–2，根据工件在毛坯中加工位置，确定生死单元格区域。

（3）将Model–1 计算结果中的应力数据映射到Model–2。

（4）运算Model–2，得到加工变形。

3 实例分析

为了说明提出的变形控制方法，选择一种典型的梁类零件用来验证，零件与毛坯如图2 所示。有限元模型材料为铝合金，PEPG 算法参数设置为种群数29，学习率0.01，初始标准差0.5。工件变形通过遍历有限元模型底面节点变形值，以最大值与最小值的差t 作为评价指标。为方便在PEPG 中梯度更新，将10/t 作为评价函数，以最大化10/t 作为优化目标。

经过多次迭代，优化模型趋于收敛，收敛过程如图3 所示。在第1 代中，最好的变形评价指标t=0.293mm。其模型力载荷数值皆为0，加工位置Z=10mm。在第4 代中，最好的变形评价指标t=0.03951mm。其模型力载荷位置A=（–9，14mm），B=（–8，6mm），C=（–1，18mm），D=（1，8mm）；力载荷为FA=–0.702N，FB=0.111N，FC=0.248N，FD=0.239N；加工位置Z=7mm。第31 代最好的变形评价指标t=0.02767mm。其模型力载荷位置A=（–10，7mm），B=（2，13mm），C=（2，20mm），D=（–7，14mm）；力载荷为FA=-0.306N，FB=0.08N，FC=–0.679N，FD=-0.983N；加工位置Z=7mm。变形云图如图4 所示。

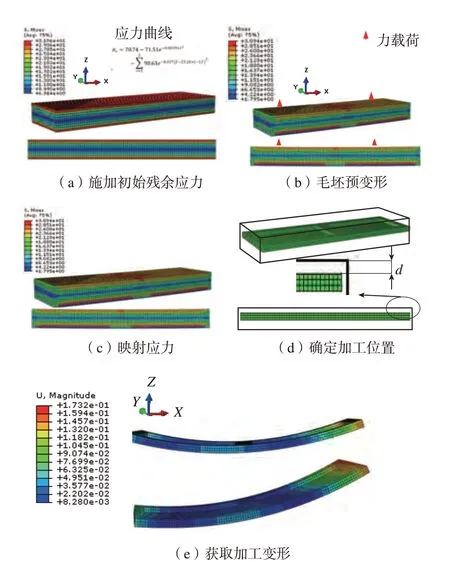
图1 仿真计算模型示意图Fig.1 Schematic diagram of simulation model

图2 工件与毛坯尺寸图（mm）Fig.2 Dimensions of workpiece and blank

通过上述分析可知，多次迭代后，变形逐步得到抑制。初始时，毛坯未受力载荷，工件加工位置Z=10mm，最终工件变形较大；第4 代时，毛坯受力载荷，发生预变形，工件加工位置Z=7mm，其加工变形明显减小；第31 代时，工件加工位置Z=7mm，与第4 代一致，但是其毛坯所受力载荷与第4 代不同，其加工变形相比第4 代减小。第31 代最终变形为0.02767mm，相比第1 代最终变形0.293mm，减小了0.26533mm，说明在预变形和加工位置两个因素共同优化的情况下，可以更有效地抑制加工变形，为加工变形的控制提供了更丰富的组合手段。

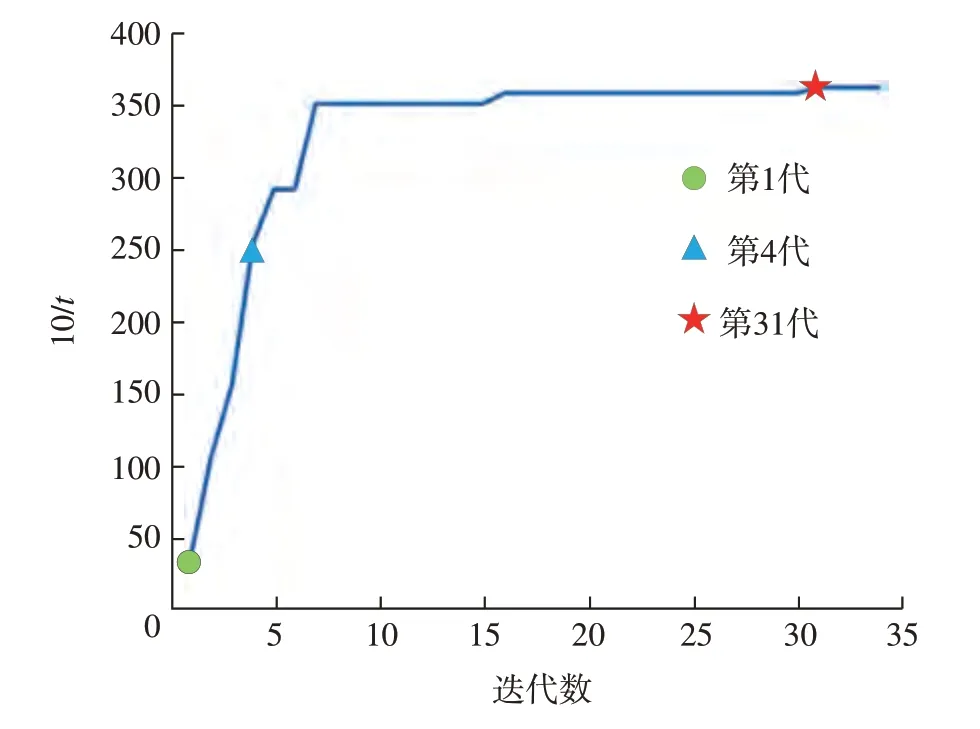
图3 迭代过程Fig.3 Iteration process

图4 变形云图Fig.4 Deformation nephogram

4 讨论

基于本文建立的加工变形控制模型，在仿真环境下获得了良好的变形控制效果。目前仿真环境下的应力曲线是根据经验给出的。由于测量手段的限制，毛坯内部残余应力的精确测评还是一大难题[21]。另外，在实际加工过程中，还存在各种难以准确预测的随机因素，如材料的属性、切削应力以及塑性变形后残余应力的变化等，都会对实际的加工变形控制带来一定的影响。而本文在仿真环境下研究预变形和零件加工位置优化的意义在于探索以上两种策略对变形控制的方法。仿真数据是基于物理模型及其规律得出的，能够为今后数据驱动的加工变形控制研究奠定基础，这也是今后需要继续探索的研究方向。

5 结论

飞机结构件的加工变形是航空制造业亟需解决的瓶颈问题之一。因此本文综合考虑毛坯预变形和加工位置两个因素，实现了对加工变形的控制。同时，以最小化加工变形为目标，采用PEPG 优化算法寻找最优参数。最终结果表明，通过毛坯预变形和加工位置同时控制加工变形，有着良好的效果。本文验证了毛坯预变形和加工位置对加工变形的重要影响，以及多因素影响下优化解仍可搜索，为以后数据驱动的加工变形控制奠定基础。虽然本文取得了良好的效果，但未来仍有许多工作要做。目前，只是在仿真环境下进行了验证，未来会在加工环境下进一步探索预变形和加工位置对加工变形控制的作用。