左删失恒定应力部分加速寿命试验下逆Rayleigh分布的参数估计

龙兵，张忠占

（1.荆楚理工学院数理学院，湖北荆门448000；2.北京工业大学应用数理学院，北京100124）

0 引 言

在可靠性寿命试验中经常会遇到一些长寿命的产品，在正常使用条件下进行试验，通常需要花费很长的时间。为了更快地获得失效数据进行可靠性分析，可以选择采用加速寿命试验，即将产品置于更严酷的应力条件下试验，这样可以加速性能的退化，使产品更快地失效。将所有的受试产品都放在加速环境下试验，称为加速寿命试验，若只放一部分产品，则称部分加速寿命试验。由恒定应力部分的加速寿命试验数据可估算得到加速因子，从而实现两种应力水平下寿命数据的转换，节省试验时间和经费，并能很快得到统计分析结果。部分加速寿命试验已经引起了一些统计学者的重视，形成了很多研究成果。ISMAIL[1-2]基于截尾样本，在恒定应力部分加速寿命试验模型下，讨论了Weibull分布的参数及加速因子的极大似然估计，确定了最优试验方案。ISMAIL等[3-4]在恒定应力部分加速寿命试验模型下，求得了II型Pareto分布和逆Weibull分布的参数及加速因子的极大似然估计，通过最小化广义渐近方差给出了两种应力水平下样本的最优分配方案。文献[5-6]也在恒定应力加速寿命试验模型下，讨论了Pareto分布和逆Weibull分布的可靠性问题。

逆Rayleigh分布作为可靠性领域的一个重要分支，其统计性质值得深入研究。针对该分布的研究成果已有很多，JEBELY等[7]在完全观测样本下讨论了逆Rayleigh分布的密度函数和分布函数的估计。文献[8-10]在完全观测样本下用贝叶斯方法研究了逆Rayleigh分布的统计推断问题。在寿命测试试验中，截尾是大多数寿命数据集不可避免的特征，NAVID等[11]讨论了在单截尾和双截尾数据下逆Rayleigh分布的贝叶斯分析。与已有文献不同，本文将基于左删失样本，在部分加速寿命试验模型下，分别用经典方法和贝叶斯方法讨论逆Rayleigh分布的统计性质，并比较这两种方法所得到的参数估计值。

1 基本假设和模型描述

在应力水平S0，S1(S0＜S1)下进行寿命试验，其中S0为正常应力水平，S1为加速应力水平。基本假设如下：

A 1 在应力水平S0,S1下，受试产品有相同的失效机理。

A2 在应力水平S0下，产品的失效时间为t；在应力水平S1下，产品的失效时间为x，满足t=βx，其中，β(β＞1)为加速因子，且t与x相互独立。

A3 在应力水平S0下，产品的失效时间t服从逆Rayleigh分布，其分布函数和概率密度函数分别为

其中，θ＞0为尺度参数。

根据假设A 1～A 3，在应力水平S1下，产品的失效时间x服从逆Rayleigh分布，其分布函数和概率密度函数分别为

即在应力水平S1下，产品的失效时间x服从参数为λ的逆Rayleigh分布。

现有n个受试产品被随机分成2组，它们的容量分别为n0,n1。其中n0个样品被安排到正常应力水平S0下进行寿命试验，n1个样品被安排到加速应力水平S1下进行寿命试验。在应力水平Si(i=0,1)下进行左删失试验：对ni(i=0,1)个产品在0时刻进行寿命试验，直到时刻τi(i=0,1)时进行观测，此时发现已经有di(i=0,1)个产品失效，但不知其失效时刻，此后进行跟踪观测，可得到剩余的mi=ni-di(i=0,1)个产品的失效时刻。设观测到的失效时刻分别为t=(t1,t2,…,tm0)（在应力水平S0下）和x=(x1,x2,…,xm1)（在应力水平S1下）。

2 极大似然估计

由上述试验数据，在应力水平S0下的似然函数为

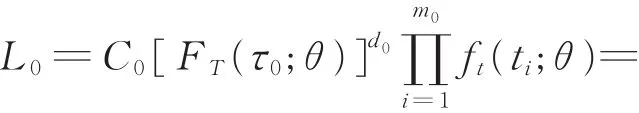
其中，C0＞ 0，且与θ无关。

在应力水平S1下的似然函数为

其中，C1＞0，且与λ无关。

由于在不同应力水平下进行的寿命试验是相互独立的，因此在左删失恒定应力部分加速寿命试验下的全似然函数为

用对数似然函数ln L求关于θ,λ的偏导数，得到似然方程组：

解得参数θ,λ的极大似然估计，分别为

由此，β的极大似然估计为

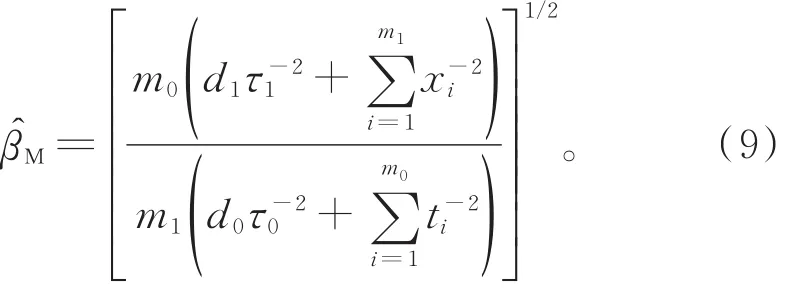
在式（9）中，令 d0=d1=0，m0=n0,m1=n1，不难得到在完全观测样本t=(t1,t2,…,tn0)和x=(x1,x2,…,xn1)下，参数 θ,λ,β的极大似然估计分别为

3 Fisher信息矩阵及近似置信区间

利用LOUIS[12]提出的缺失信息原则，计算观测到的Fisher信息矩阵。缺失信息原则的概念可表述为观测信息=完全信息-遗失信息。

记 η=(θ,β)，W 表示完全数据，X 表示观测数据，IW(η)为完全信息矩阵，IX(η)为观测信息矩阵，IW|X(η)为遗失信息矩阵，则观测信息矩阵为

在完全数据情形下计算得到的完全信息矩阵为

在应力水平S0下，记Y=(Y1,Y2,…,Yd0)，则Y表示受试样品在区间(0,τ0)内失效时刻构成的向量，由于无具体的值，因此视为遗失数据。同理，在应力水平S1下，记Z=(Z1,Z2,…,Zd1)，且Z表示受试样品在区间(0,τ1)内失效时刻构成的向量。

根据条件密度公式，得到Yj(j=1,2,…,d0)的概率密度函数为

遗失信息矩阵为

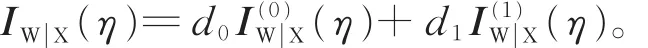
在应力水平 S0下，观测区间 (0,τ0)的 Fisher信息矩阵为

在应力水平 S1下，观测区间 (0,τ1)的 Fisher信息矩阵为

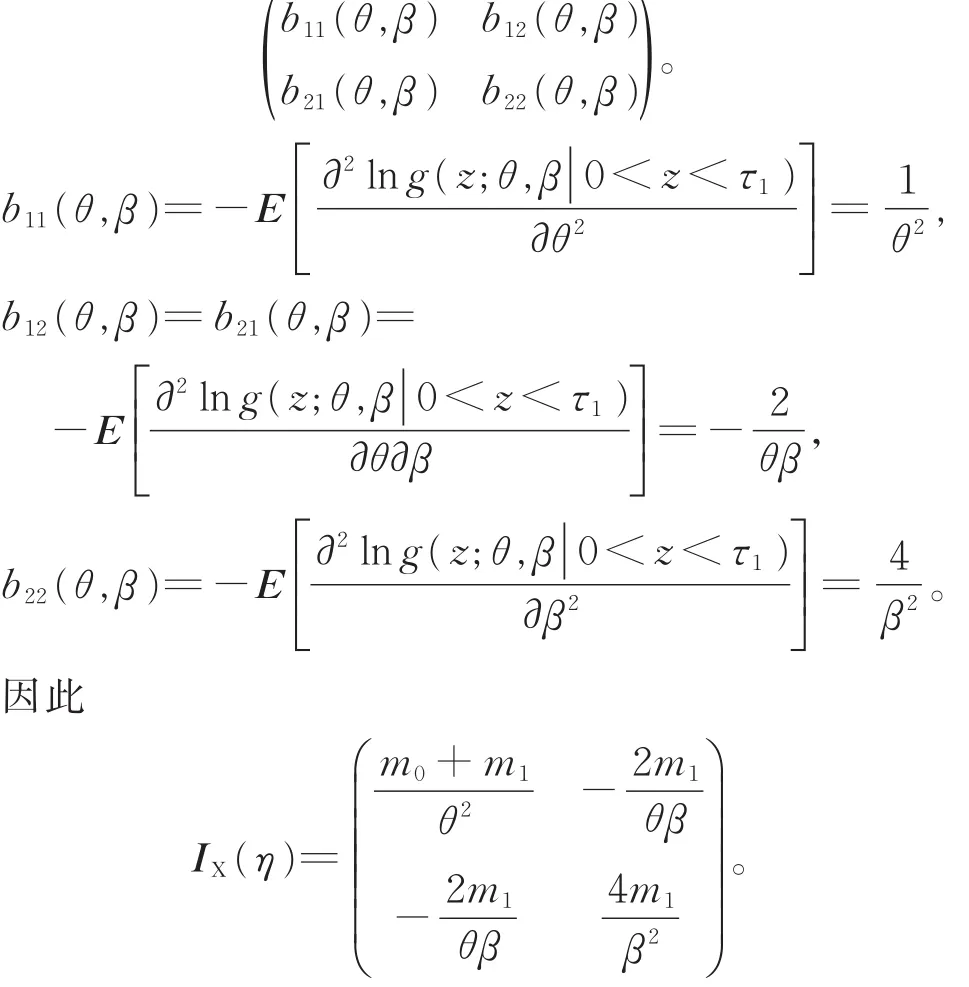
由文献[13]知，当样本量很大时，参数的极大似然估计 (θ̂M,β̂M)渐近服从二元正态分布，且期望为(θ,β)，方差、协方差矩阵为I-1X(η̂)（观测信息矩阵IX(η̂)的逆矩阵），于是有

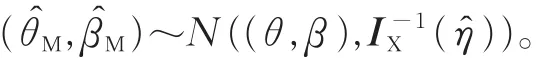
因此，参数θ,β的置信水平为100(1-γ)%的近似置信区间，分别为

其中，U11和U22为方差、协方差矩阵的主对角线元素，Zγ/2为标准正态分布的γ/2上分位数。

4 参数的贝叶斯估计

当有先验信息可以利用时，采用贝叶斯方法通常可以提高估计的精度，因此，本节将计算参数θ和加速因子β的贝叶斯估计。

取参数θ的先验密度为

其中a0＞0为超参数。由式（7）和式（11）及贝叶斯公式，可得θ的后验密度为

在平方损失函数下，θ的贝叶斯估计为

由于在应力水平S0下，产品的可靠度函数为

因此，在平方损失函数下R0(t)的贝叶斯估计为

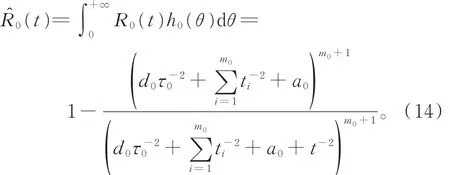
取参数λ的先验密度为

其中a1＞0为超参数。由式（8）和式（15），可得λ的后验密度：

由式（17）无法求出显式解，可用数值积分求解。

下面用极大似然法估计超参数a0,a1。

在应力水平S0下，根据先验分布π0(θ)，可得到经验分布：

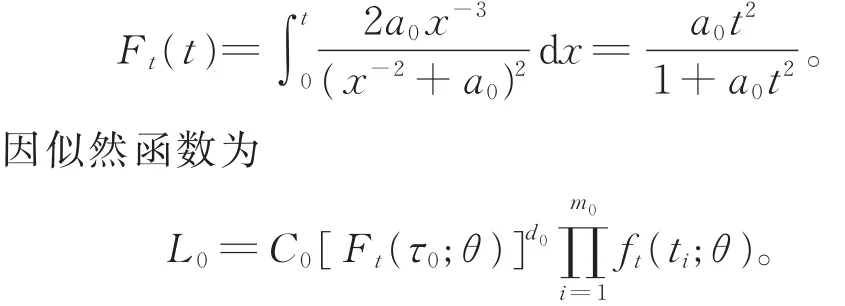
以 Ft(τ0),ft(ti)分 别 代 替 上 式 中 的Ft(τ0;θ),[ft(ti;θ )]，则有

记式（19）的最终迭代值为 â0。

用类似的方法可求得超参数a1的估计值，记为â1。将 â0,â1代入式（13）、（14）、（17），就可求得相应的贝叶斯估计值。

5 Monte Carlo模拟

对于不同的 n0,n1,θ,λ，从均方误差（MSE）角度考虑分布参数和加速因子的估计性质。模拟过程如下：

第1步给定n0,n1及参数θ,λ的值。

第2步产生一个容量为n且服从均匀分布U(0,1)的独立同分布样本U1,U2,…,Un，令

ti=(-θ/ln Ui)1/2，i=1,2,…,n0，

xi=(-λ/ln Ui)1/2,i=n0+1,n0+2,…,n0+n1，则(t1,t2,…,tn0)(xn0+1,xn0+2,…,xn0+n1)就是分别来自于逆Rayleigh分布式（1）和式（5）的样本。

第3步给定τ0,τ1的值，得到左删失样本。

第4步基于上面得到的左删失样本，分别计算θ,β的点估计。

第5步步骤2～步骤4重复1 000次，计算θ,β的均方误差。

第 6步在不同的 n0,n1,θ,λ,τ0,τ1下，重复上述过程。

将以上步骤产生的随机模拟结果列于表1，从表1中可以看到，随着n0,n1的增加，参数θ,β的极大似然估计和贝叶斯估计的均方误差逐渐减小，说明极大似然估计具有大样本性质。在小样本场合，贝叶斯估计要明显优于极大似然估计，随着样本量的增加，两者的差距逐渐缩小。为了比较左删失样本下和完全观测样本下参数估计精度的差异，当θ=2，λ=1时，模拟计算了不同样本容量下参数θ,β估计的均方误差（见表2），结果显示，完全观测样本下参数估计的精度要优于左删失样本。

为了了解在具体样本下各种估计的效果，取θ=3，λ=2，通过随机模拟的方式分别产生容量为40和50的服从逆Rayleigh分布的样本，在应力水平S0下（θ=3），按从小到大的顺序排列：

0.914 ，1.017，1.102，1.109，1.148，1.194，1.277，1.309，1.341，1.381，1.416，1.502，1.515，1.673，1.674，1.687，1.713，1.834，1.875,1.922，2.125，2.211，2.245，2.427，2.617，2.859，2.918，3.022，3.062，3.489，3.567，3.571，3.601，3.725，3.787，3.935，4.965，5.098，5.633，6.288。

在应力水平S1下（λ=2），按从小到大的顺序排列：0.784，0.793，0.887，0.938，1.056，1.093，1.098，1.108，1.109，1.144，1.184，1.192，1.235，1.253，1.255，1.261，1.263，1.382，1.389，1.401，1.410，1.427，1.451，1.485，1.505，1.513，1.515，1.538，1.546，1.608，1.643，1.673，1.767，1.787，1.884，1.949，2.014，2.192，2.368，2.552，2.792，3.012，3.042，3.065，4.501，4.841，5.121，5.758，6.142，8.505。

表1 左删失样本下参数估计的均方误差Table 1 Mean square errors of parameter estimation under left censored samples

表2 完全观测样本下参数估计的均方误差Table 2 Mean square errors of parameter estimation under complete observation samples

表3 参数的点估计及置信区间Table 3 Point estimation and confidence interval of the parameters

由τ0，τ1得到左删失样本，计算θ,β的极大似然估计、贝叶斯估计及置信水平为95%的置信区间，并分别记为θ̂M，θ̂B，(θ̂L,θ̂U)和β̂M,β̂B，(β̂L,β̂U)，相应的估计结果见表3。

由于参数真值θ=3,β=1.224 7，从表3的数据中可知，参数的贝叶斯估计比极大似然估计更接近参数真值，参数真值位于置信区间内。通常，随着左删失数据的增多，参数估计值与真值之间的差值以及置信区间的长度呈逐渐变大趋势。

6 结 语

加速寿命试验是利用产品寿命和应力水平之间的某种已知函数关系，估算产品在正常应力水平时的寿命。当产品寿命和应力水平之间的关系未知时，可采用恒定应力部分加速寿命试验，此方法更适合新产品。用两种应力水平下的试验数据估计加速因子，然后将高应力水平下的寿命转换为正常应力水平时的寿命。近年来，部分加速寿命试验已被应用于可靠性统计推断。在本文中，当产品的失效时间服从逆Rayleigh分布时，基于恒定应力部分加速寿命试验数据，得到了分布参数和加速因子的极大似然估计及贝叶斯估计。由遗失信息原则计算极大似然估计的渐近方差，得到参数的近似置信区间。通过数值模拟说明样本量对估计精度的影响，并将极大似然估计与贝叶斯估计做了比较，结果表明，在小样本场合，贝叶斯估计要优于极大似然估计。