Stability of Viscoelastic Wave Equation with Structural δ-Evolution in Rn

A.Beniani,Kh.Zennirand A.Benaissa

1 Center University of Belhadj Bouchaib-B.P.284 RP,Ain Temouchent 46000,Algeria

2 Department of Mathematics,College of Sciences and Arts,Qassim University,Ar-Rass,Saudi Arabia

3 Laboratory ACEDP, University of Djillali Liabes-B. P. 89, Sidi Bel Abbes 22000,Algeria

Abstract. The aim of this paper is to study the Cauchy problem for the viscoelastic wave equation for structural δ-evolution models. By using the energy method in the Fourier spaces,we obtain the decay estimates of the solution to considered problem.

Key Words: Viscoelatic wave equation,Fourier transform,Lyapunov functions,Decay rates.

1 Introduction

Cavalcanti et al.[3]studied the equation

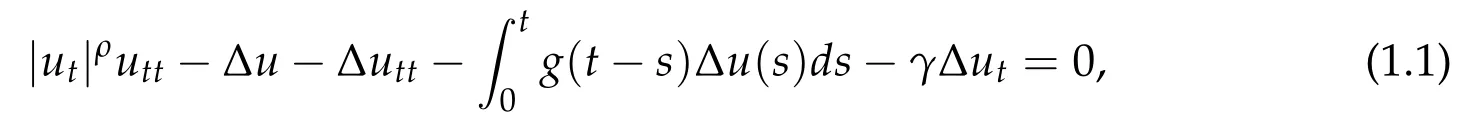
with x ∈Ω, t ＞0, ρ ＞0. They proved a global existence result for γ ≥0, and an exponential decay for γ ＞0. This last result has been extended to a situation, where a source term is competing with the strong damping mechanism and the one induced by the viscosity. For more details see[9]. The authors combined well known methods with perturbation techniques to show that a solution with positive small energy exists globally and decay to the rest state exponentially.

In any spaces dimension,the paper[13]treated the viscoelastic wave equation

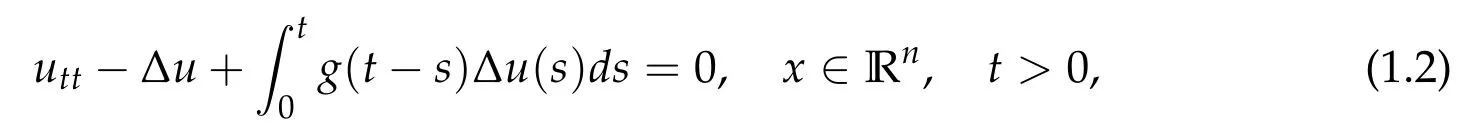
where g,being positive and nonincreasing,is the relaxation function which describes the material in consideration and u0= u(x,0) and u1= ut(x,0) are given data. By using the energy method in the Fourier spaces, the general decay estimates of the solution is shown. In[17],the author considered the following equation

where q,n ≥2 and M is a positive C1-function satisfying for

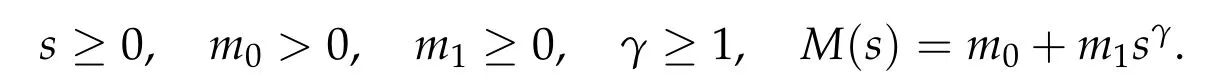
In order to compensate the lack of Poincar´e’s inequality in Rnand for wider class of relaxation functions, the author used the weighted spaces to establish a very general decay rate of solutions of viscoelastic wave equations in Kirchhoff-type.

In[5],the author looked into a linear Cauchy viscoelastic equation with density. His study included the exponential and polynomial rates,where he used the spaces weighted by density to compensate for the lack of Poincar´e’s inequality. The same problem treated in[5],was considered in[7],where it id considered a Cauchy problem for a viscoelastic wave equation. Under suitable conditions on the initial data and the relaxation function,they prove a polynomial decay result of solutions. The used conditions on the relaxation function g and its derivative g′are different from the usual conditions.

Recently, in [8], the authors considered the weak-viscoelastic case in the following problem,

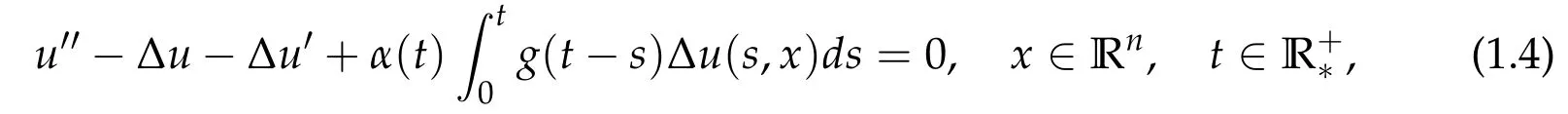
where n ≥2. The energy decay results were established for weak-viscoelastic wave equation in Rn, which depends on the behavior of both α and g. The main idea of the proof was to construct an appropriate Lyapunov function of the system obtained after taking the Fourier transform.

To extend previous results, we study the decay rate of the solution to the Cauchy problem for structural damped δ-evolution with memory term in Fourier spaces

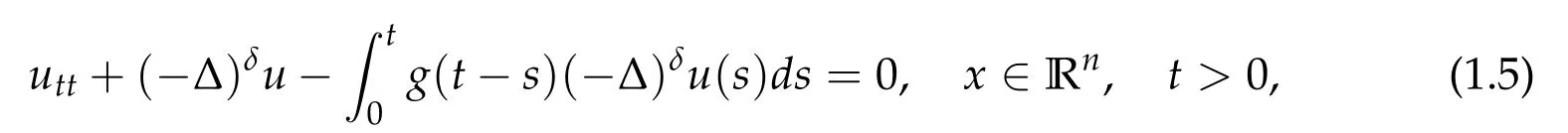
with the initial conditions

The model here considered are well known ones and refer to materials with memory as they are termed in the wide literature which is concerned about their physical,mechanical behavior and the many interesting analytical problems. The physical characteristic property of such materials is that their behavior depends on time not only through the present time but also through their past history.

2 Preliminaries and assumptions and Asymptotic stability

For a later use,we have the following lemma,which is useful in obtaining our estimate of solutions in the Fourier space.

Lemma 2.1([8]). For any f ∈C1(R+)and any h ∈H1(R+),we have

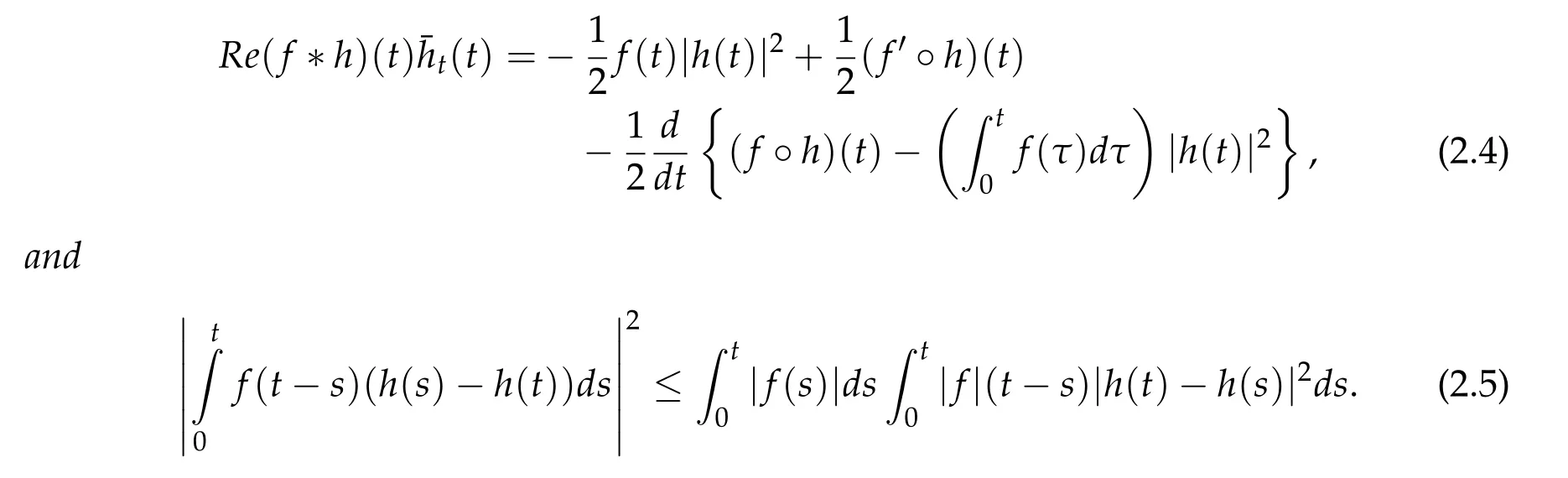
The following Lemma is very useful in the sequel.

Lemma 2.2([15]). Assume that β(t)＞0 for all t ≥0,l,p ≥2. Then we have

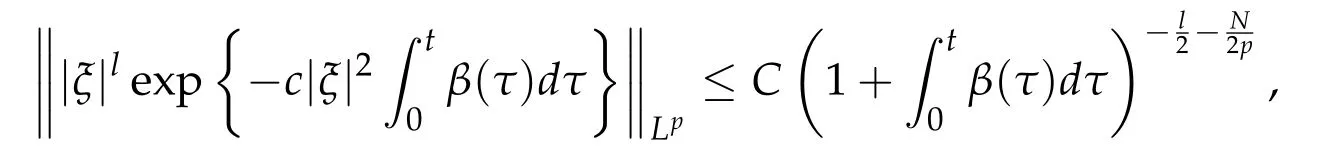
where C is a positive constant.

Our aim is to obtain the decay estimates of the solution to the problem (1.5)-(1.6).After Fourier transformation of(1.5)-(1.6),we get the following system

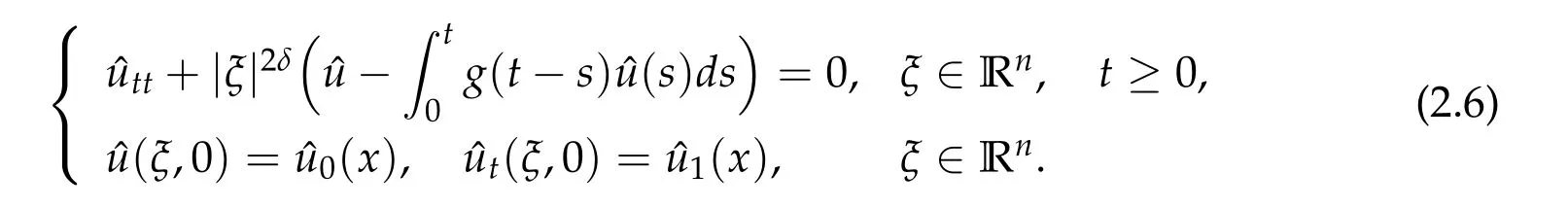
The energy associated to(2.6)is given by

Lemma 2.3. The modified energy associated to(2.6)is defined as follows.

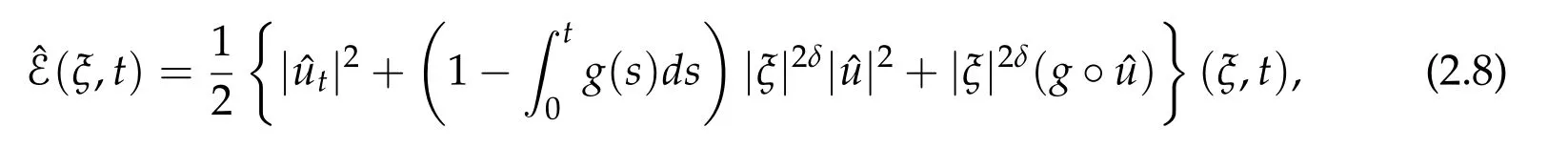
and the modified energy ˆE(ξ,t)is non-increasing and satisfies for all t ≥0

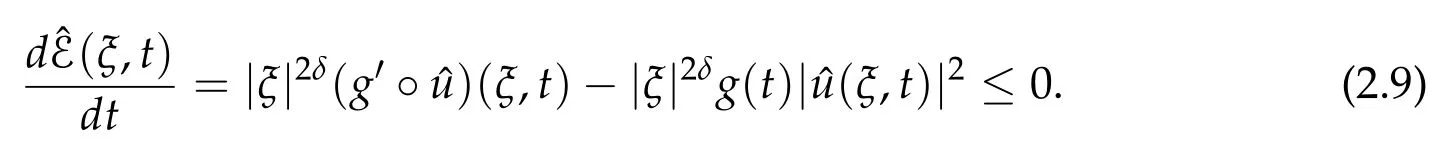
Proof. Multiplying the equation in(2.6)by ¯ˆutand taking the real part,we get

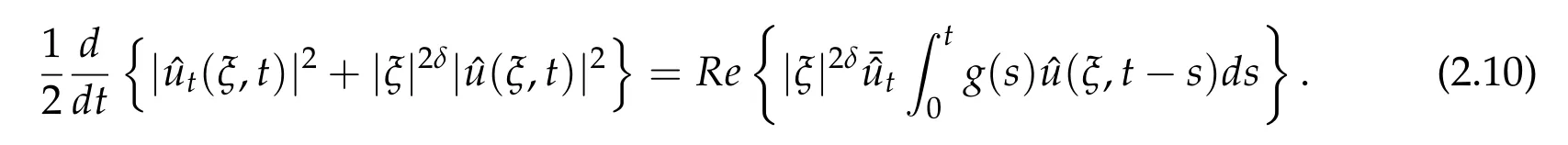
Using Lemma 2.1,we easily see that

As he stood on the gallows40 he said: Every one doomed41 to death has the right to speak once before he dies; and I too have that privilege? Yes, said the King, it shall be granted to you

Substituting this last equality into(2.10),the identity(2.9)then follows.

On the other hand,using(A1)there exists a positive constant c1＞0 such that,for all t ≥0 and for all ξ ∈Rn,we have

Thus,we complete the proof.

We will prove the following exponential stability result.

Proposition 2.1. Let ˆu(ξ,t)be the solution of (2.6). Then there exist two positive constants C,β0such that

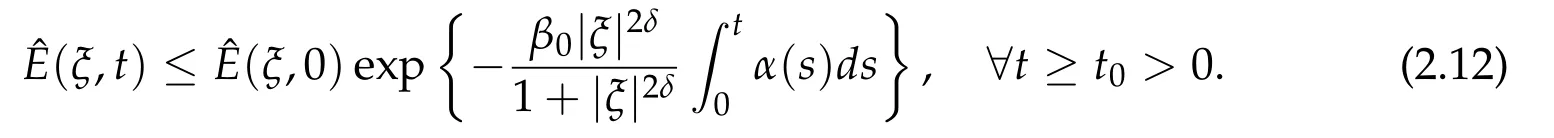
To prove Proposition 2.1,the key point is to apply the multiplier techniques in Fourier spaces in order to obtain useful estimates and prepare some functionals associated with the nature of our problem to introduce an appropriate Lyapunov functional.

Proof. Multiplying(2.6)by ¯ˆu and taking the real part,we get

At this point, we choose η large enough such that (2.20) holds and η-c2＞0. Consequently(2.21)yields

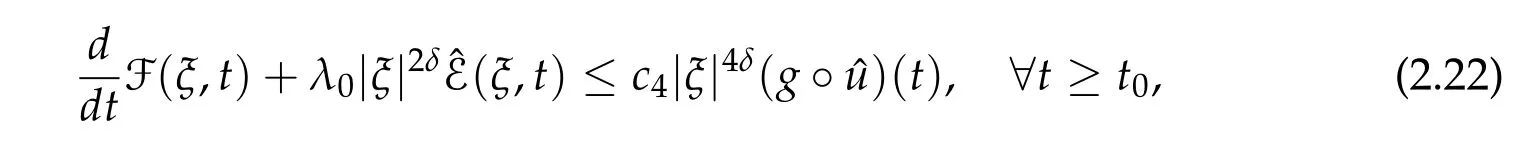
for some λ0,c4＞0.

Multiplying(2.22)by α(t)and making use of(2.2),we get

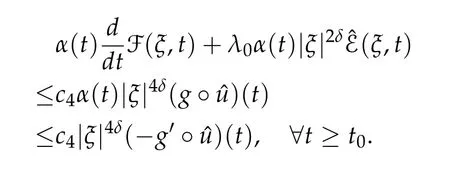
Exploiting(2.9),we have

This gives

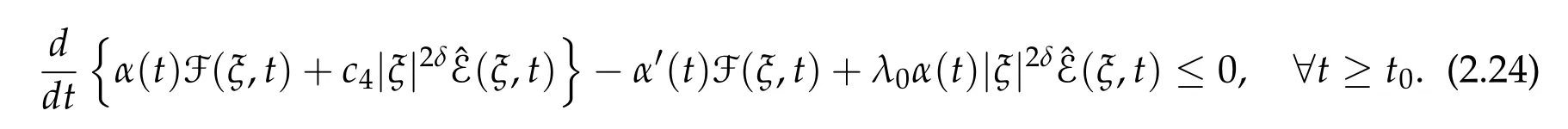
Recalling that α′(t)≤0 and setting

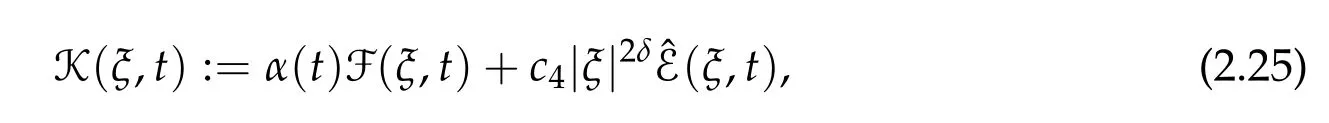
we get

On the other hand,since α(t)is bounded,we deduce that

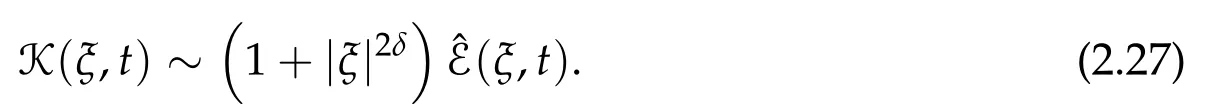
These last two estimates lead to

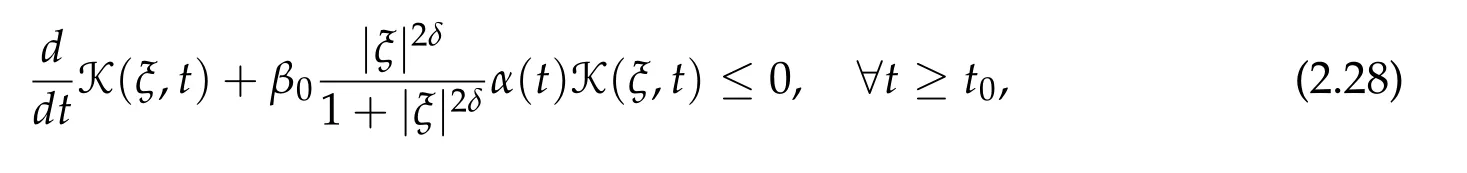
for some β0＞0. Integrating(2.28)with respect to t yields

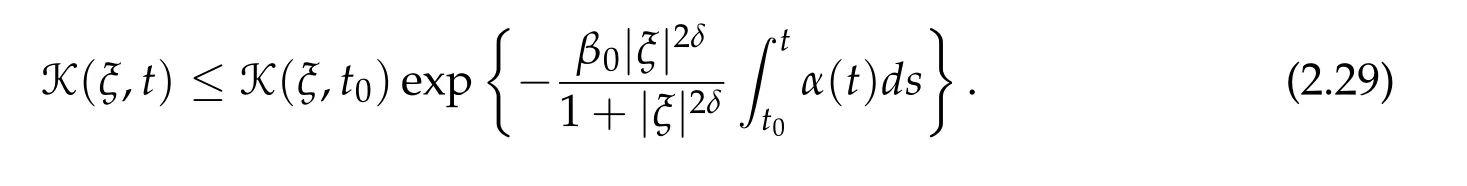
Thus,using(2.27),we obtain

Finally, the estimate (2.12) holds by combining (2.11) and (2.30). This finishes the proof of Proposition 2.1.

Thus our main result reads as follows:

where C and c are two positive constants and k ≤σ.

where we have used Lemma 2.2

On the other hand,

Collecting (2.33) and (2.34), then the estimate (2.31) holds. This completes the proof of Theorem 2.1.

Acknowledgements

The authors wish to thank deeply the anonymous referees for their useful remarks and their careful reading of the proofs presented in this paper.