Existence and Uniqueness of Solution for a Class of Nonlinear Degenerate Elliptic Equations

Albo Carlos Cavalheiro

Department of Mathematics,State University of Londrina,Londrina,Brazil

Abstract. In this work we are interested in the existence and uniqueness of solutions for the Navier problem associated to the degenerate nonlinear elliptic equations

Key Words: Degenerate nonlinear elliptic equation,Weighted Sobolev spaces.

1 Introduction

where Ω is a bounded open set in Rn, ω1, ω2, v1and v2are four weight functions, Δ is the Laplacian operator and 2 ≤q,s ＜r ＜p ＜∞.

Let Ω be an open set in Rn. We denote by W(Ω) the set of all measurable, a.e. in Ω positive and finite functions ω = ω(x), x∈Ω. Elements of W(Ω) will be called weight functions. Every weight ω gives rise to a measure on the measurable subsets of Rnthrough integration. This measure will be denoted by μω. Thus,

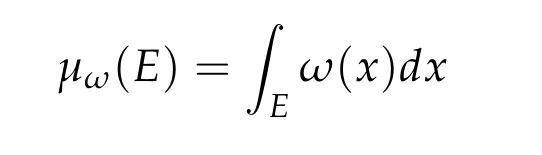
for measurable sets E⊂Rn.

In general,the Sobolev spaces Wk,p(Ω)without weights occur as spaces of solutions for elliptic and parabolic partial differential equations. For degenerate partial differential equations,i.e.,equations with various types of singularities in the coefficients,it is natural to look for solutions in weighted Sobolev spaces(see[1-3,5,10]and[15]).

A class of weights, which is particularly well understood, is the class of Ap-weights(or Muckenhoupt class)that was introduced by B.Muckenhoupt(see[12]). These classes have found many useful applications in harmonic analysis(see[14]). Another reason for studying Ap-weights is the fact that powers of the distance to submanifolds of Rnoften belong to Ap(see[11]). There are,in fact,many interesting examples of weights(see[10]for p-admissible weights).

In the non-degenerate case(i.e.,with ω(x)≡1),for all f ∈Lp(Ω)the Poisson equation associated with the Dirichlet problem

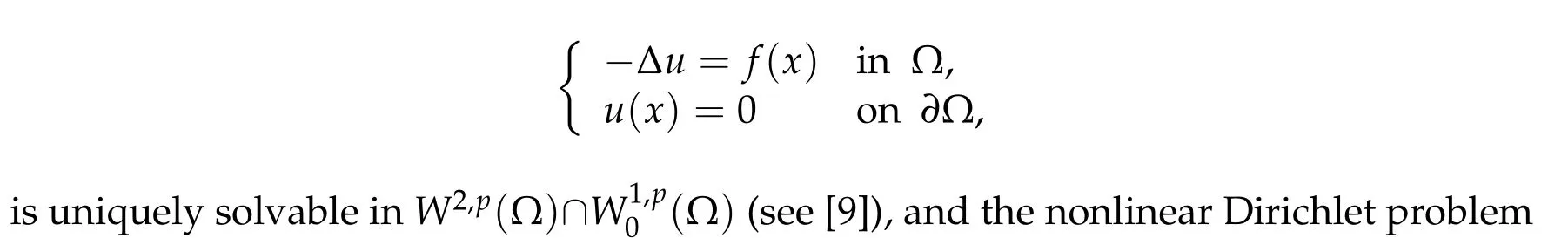
has been studied by the author in[2].

The following theorem will be proved in Section 3.

2 Definitions and basic results

Remark 2.2. In this paper,we will use many times the following Convergence Principle in Banach spaces: Let X be a Banach space, x∈X and a sequence {xn} in X. If every subsequence of{xn}has,in turn,a subsequence which converges strongly to x,then the original sequence converges strongly to x, i.e., xn→x as n →∞(see [16], Proposition 10.13).

3 Proof of Theorem 1.1

The basic idea is to reduce the problem (P) to an operator equation Au = T and apply the theorem below.

Theorem 3.1. Let A : X→X*be a monotone,coercive and hemicontinuous operator on the real,separable, reflexive Banach space X. Then for each T∈X*the equation Au = T has a solution u∈X.

Acknowledgements

The author would like to thank the referee for his/her useful suggestions and comments which have improved the presentation of the paper.