A Note on Rough Parametric Marcinkiewicz Functions

Laith Hawawsheh,Ahmad Al-Salmanand Shaher Momani

1 School of Basic Sciences and Humanities, German Jordanian University, Amman,Jordan

2 Department of Mathematics,Sultan Qaboos University,P.O.Box 36,Al-Khod 123 Muscat,Sultanate of Oman

3 Department of Mathematics, Faculty of Science, University of Jordan, Amman 11942,Jordan

4 Department of Mathematics and Sciences,College of Humanities and Sciences,Ajman University,Ajman,UAE

Abstract. In this note, we obtain sharp Lp estimates of parametric Marcinkiewicz integral operators. Our result resolves a long standing open problem. Also,we present a class of parametric Marcinkiewicz integral operators that are bounded provided that their kernels belong to the sole space

Key Words:Marcinkiewicz integrals,parametric Marcinkiewicz functions,rough kernels,Fourier transform,Marcinkiewicz interpolation theorem.

1 Introduction

In light of Theorem 1.1,it is clear that the dependence of the Lpbounds on α in Theorem 1.2 is not sharp. More precisely,we have the following long standing natural open problem:

Problem:

(a) Is the power(-1/2)of α in Theorem 1.1 sharp?

(b) Does the result in Theorem 1.2 hold with power of α greater than(-1)?

It is our aim in this note to consider this problem. In fact, we shall prove the following result which completely resolves the above problem:

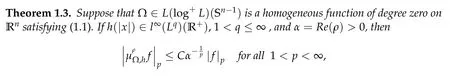
where C is independent of ρ and f. Moreover,the power(-1/p)is sharp in the sense that it can not be replaced by larger power.

Throughout the rest of the paper the letter C will stand for a constant but not necessarily the same one in each occurrence.

2 Proof of main result

This section is devoted to present a proof of Theorem 1.3. We start by recalling the following well known interpolation theorem:

Theorem 2.1([8]). Let T be a sublinear operator satisfying

3 Further study

Acknowledgements

The work is a part of the first author’s PhD thesis,which had been done under the supervision of the second and third authors.