H¨older Continuity of Spectral Measures for the Finitely Differentiable Quasi-Periodic Schr¨odinger Operators

Mei Sun and Xueyin Wang

Institute of Applied System Analysis,Jiangsu University,Zhenjiang,Jiangsu 212013,China

Key Words: Schr¨odinger operator,quasi-periodic,almost reducibility,finitely differentiable.

1 Introduction

In this paper,we consider the Schr¨odinger operators defined on ℓ2(Z)

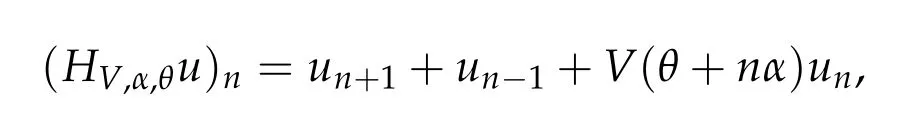
where V : Td→R is the potential, θ ∈Td= (R/Z)dis the phase, and α ∈Tdis the frequency.

These operators have been extensively and thoroughly studied for the deep connection with quasi-crystal and quantum Hall effects[11,18].This paper concerns the regularity of the spectral measure of the quasi-periodic Schr¨odinger operators. For the analytic potential V ∈Cω(Td,R), there is some significant progress [5,21,24]. However for the smooth potential V ∈Ck(Td,R),there is no similar result as far as we know,so we will give a supplementary answer to this situation.

Let us review some results on the H¨older continuity of the integrated density of states(IDS)and the individual spectral measures.

1.1 H¨older continuity of IDS

1.2 H¨older continuity of the spectral measure

Theorem 1.1. Let α ∈DCd(γ,τ), V ∈Ck(Td,R) with k ≥5Dτ and D is a numerical constant. There exists ～ε= ～ε(γ,τ,k)such that if‖V‖k≤～ε,then for any f ∈ℓ2(Z)∩ℓ1(Z),

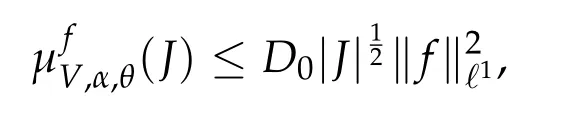
for all intervals J and all θ,where D0= D0(V,α)＞0.

Remark 1.1. Note that Theorem 1.1 is perturbative,i.e.,the smallness ～ε depends not only on the potential V,but also on the frequency α. From a counterexample of Bourgain[8],one can not expect non-perturbative results in multi-frequency case.

2 Preliminaries

2.1 Uniform hyperbolicity

Given A ∈Cω(Td,SL(2,C)) and α ∈Rdrationally independent, one can define the quasi-periodic(Q-P)cocycle(α,A):

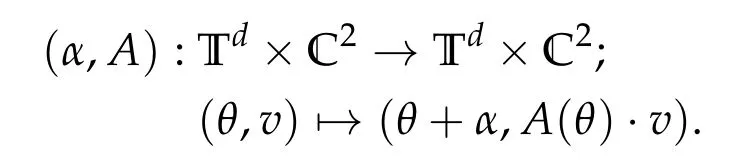
The iterations of(α,A)are of form(α,A)n=(nα,An),where

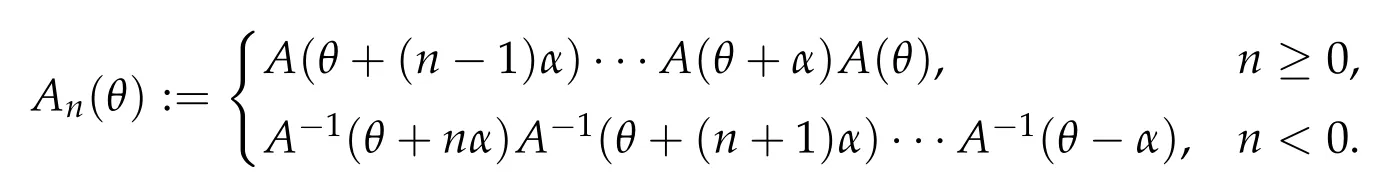
The Lyapunov exponent of the cocycle(α,A)is defined as

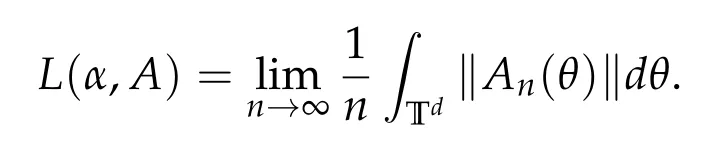
We say the cocycle (α,A) is uniformly hyperbolic if for every θ ∈Td, there exists a continuous splitting C2= Es(θ)⊕Eu(θ)such that for every n ≥0,

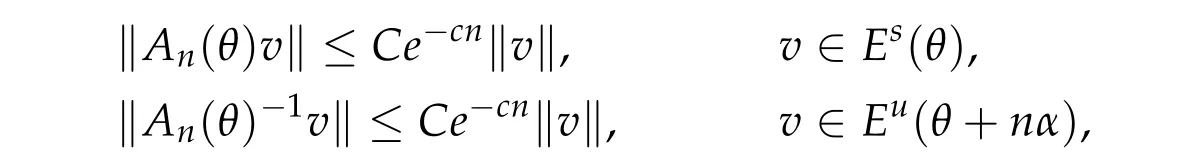
for some constants C,c ＞0. And the splitting is invariant by the dynamics:

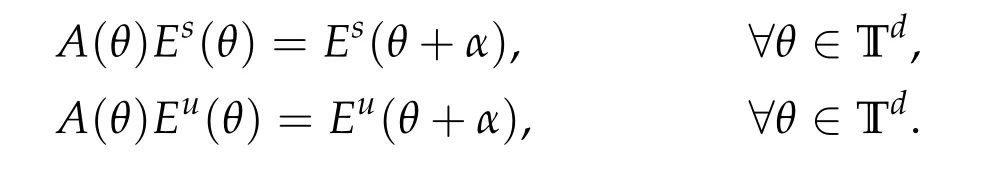
2.2 Spectral measure and Wely’s m function

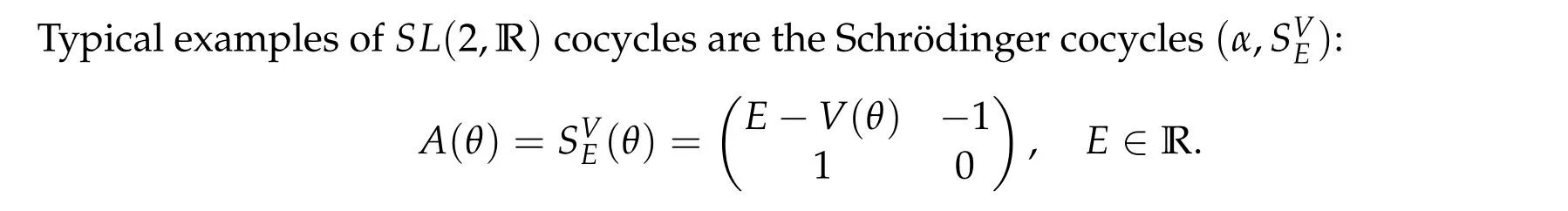
Those cocycles come from the eigenvalue equation of one dimensional quasi-periodic Schr¨odinger operators on ℓ2(Z):

2.3 Analytic approximation

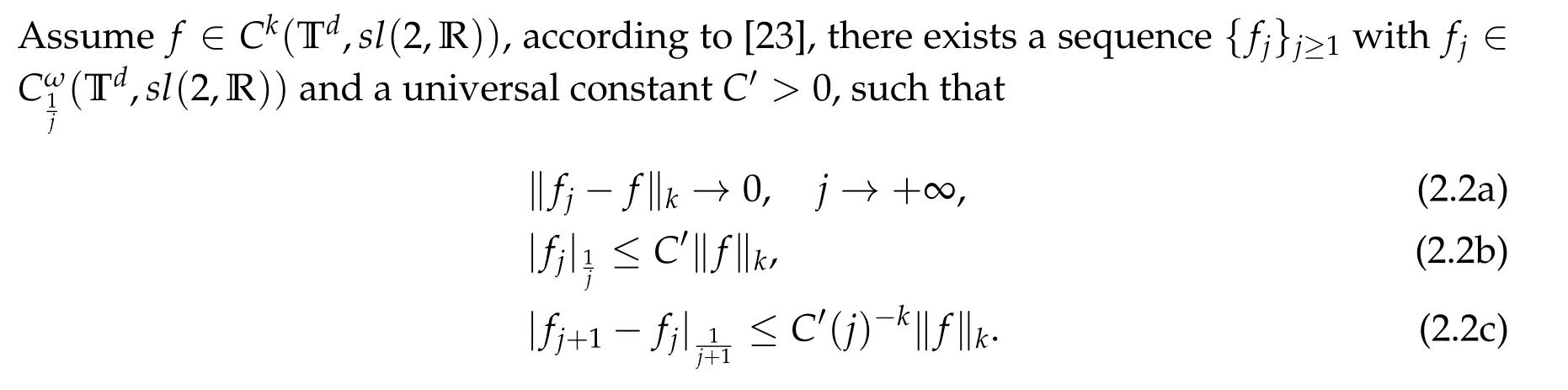
2.4 Space decomposition

3 Dynamical estimates of Ck quasi-periodic cocycles

To deal with the almost reducibility of the Ckcocycles,the strategy used here is treating the analytic cocycles firstly and turning the estimates of analytic cocycles into those of finitely differentiable cocycles by analytic approximation.

Consider the following Q-P SL(2,R)cocycle

3.1 Real quantitative estimates for Ck Q-P cocycles

3.2 Complex almost triangularization for Ck Q-P cocycles

In Theorem 3.1, one can see that the conjugation Blj: 2Td→SL(2,R) is real, which results in Aljbeing real. In fact, we can choose the complex conjugation Blj: 2Td→SL(2,C) to make Aljcomplex almost triangularization provided that the cocycle is not uniformly hyperbolic.

4 Sharp H¨older continuity of the spectral measure

where As(θ) = A(θ+(s-1)α)···A(θ+α)A(θ). Pnis an increasing family of positive self-adjoint operators. ‖Pn‖ is unbounded since trPn≥2n. Moreover, det Pnis also unbounded. For simplicity,we will use the notation a ≈b which denotes that there exist some constants C ＞0 such that C-1a ≤b ≤Ca and also use the notation a ≾b which denotes a ≤Cb for some constants C ＞0.

Acknowledgements

The authors want to thank Jiangong You and Qi Zhou for useful discussions. Mei Sun was supported by National Nature Science Foundation of China grant(No.71774070).