Multiple Non-Axially Solutions to a Mean Field Equation on S2

Zhuoran Du,Changfeng Gui,Jiaming Jin and Yuan Li

1 School of Mathematics,Hunan University,Changsha,Hunan 410082,China

2 Department of Mathematics,University of Texas at San Antonio,TX78249,USA

Abstract. We study the following mean field equation

Key Words: Mean field equation,non-axially solutions,bifurcation.

1 Introduction

In this paper,we consider the mean field equation on the unit sphere

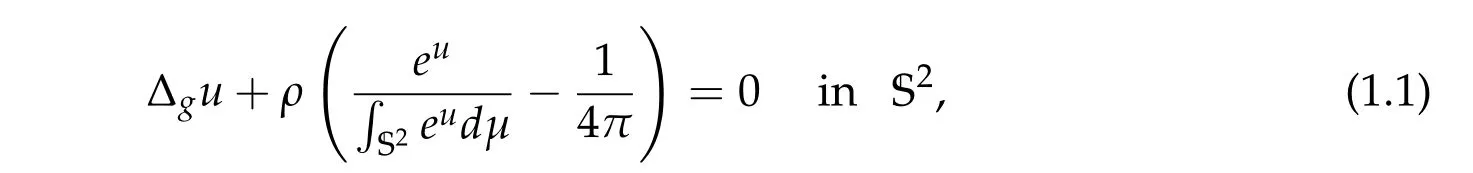
where ρ is a real parameter, Δgstands for Laplace-Beltrami operator on S2associated to the metric g inherited from the ambient Euclidean metric and dμ is the volume form with respect to g. Since the above equation is invariant by adding a constant to a solution,we introduce

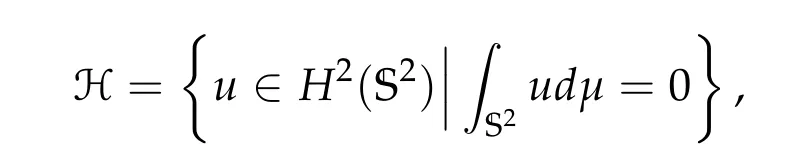
where H2(S2)is the classical sobolev space.Note that H,equipped with the H2(S2)norm,is a Hilbert space. We write S2in the following coordinate system

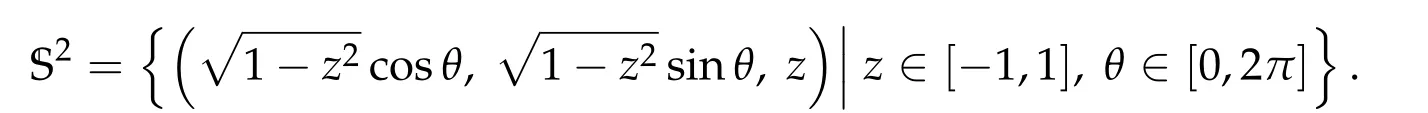
The study of existence of solution for mean field equations possess a long history and huge literature. This kind equations arise from Onsager’s vortex model for turbulent Euler flows,see[20]. They also arise from the Chern-Simons-Higgs model vortex when some parameter tends to zero,we refer the reader to[3,25-27].

inequality”, Shi, Sun, Tian and Wei [24] proved that even solution to (1.1) is unique for ρ=24π. More results under various conditions are also obtained in[12].

In this paper, for Eq. (1.1), we will generalize the axially symmetric solutions case in [9] to non-axially symmetric solutions case. Precisely, we will use the bifurcation method to obtain the multiplicity result for non-axially symmetric solutions, which are bifurcating from some points ρ with the form of 8πN. However,the applicability is not all trivial. The main difficulty is that the kernel of the nature associated operator is not one dimensional. In order to overcome this obstacle, we follow the method from[2]by searching for spaces with some symmetry. Multiple two-dimensional solutions of mean field equation on flat tori bifurcating from trivial solution can be seen in[10].

Our main results in this paper are the existence of multiple bifurcation curves and their local convexities near bifurcation points as follows.

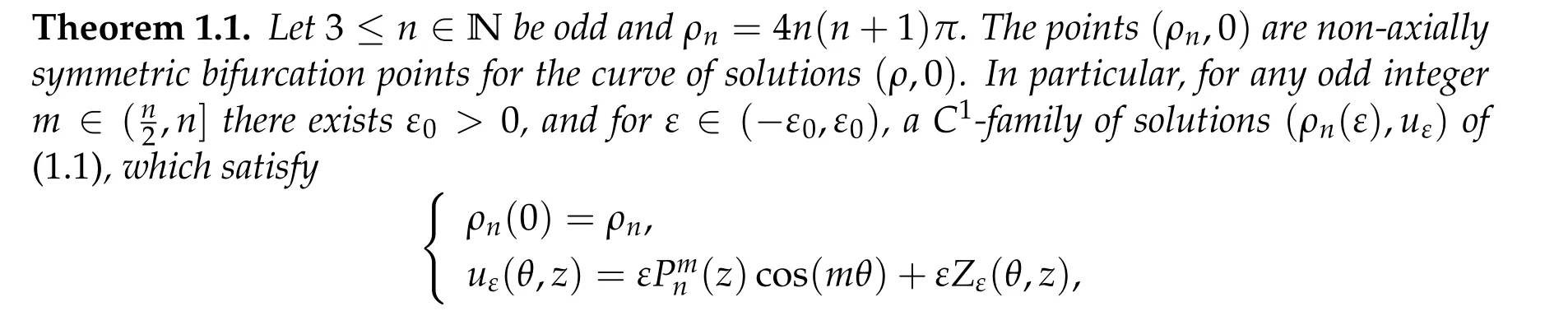
where Zε(θ,z)is uniformly bounded in L∞(S2)and Z0= 0. Moreover the bifurcation is global and the Rabinowitz alternative holds true,i.e.,a global continuum of solutions to(1.1)either goes to infinity or meets the trivial solution curve(ρ,0)at ρ= ρk,k/= n.

The following Legendre functions are solutions to (1.4) when m,n ∈N, m ＞n and play a similar role as the Legendre polynomials(1.3)

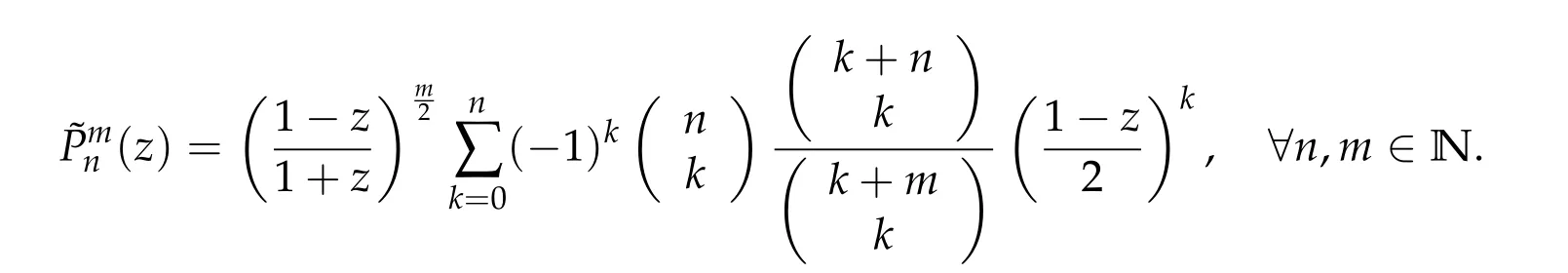
2 Preliminaries

This section contains several properties which will be used to prove Theorems 1.1 and 1.2.

Proposition 2.1. The following eigenvalue problem

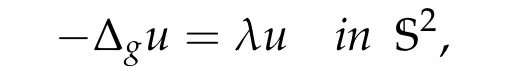
has a nontrivial bounded solution if and only if λ = λn:= n(n+1). Each eigenvalue λnhas multiplicity 2n+1 and a basis for its eigenspace is given by

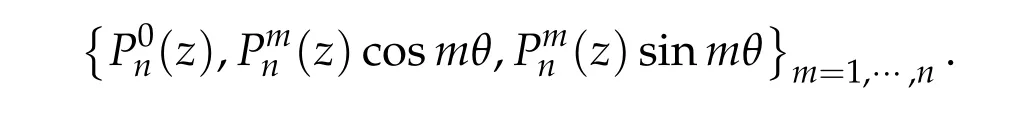
Let F(t,x) be an operator mapping from R×X to Y. Denote ∂xF and ∂tF as the Fr´echet partial derivatives of F with respect to x and t respectively.

3 Non-axially symmetric solutions

In this section we first apply Proposition 2.2 to prove Theorem 1.1. Define an operator T :R×H →L2(S2)as

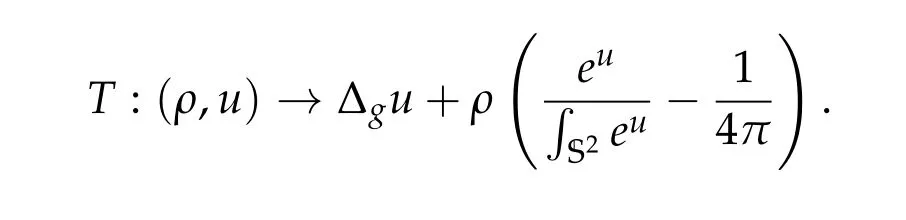
Direct computation shows that

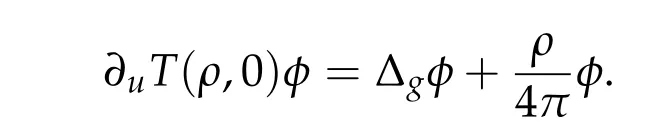
We set

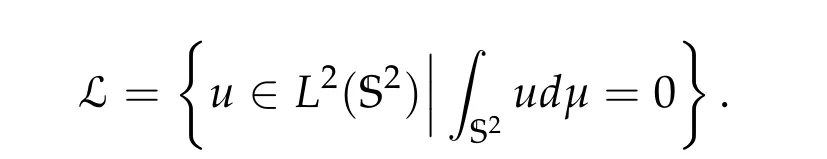
Clearly T maps T :R×H into L.

Lemma 3.1. Assume ρ= ρn=4n(n+1)π,n ∈N,then the dimension of the space of bounded solutions to ∂uT(ρ,0)φ=0 is 2n+1,and the kernel is

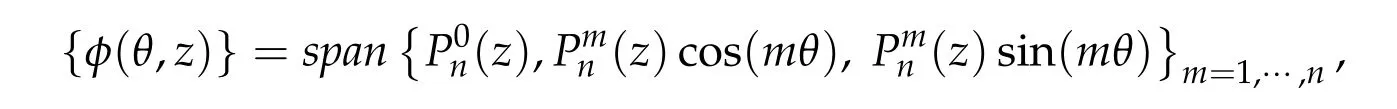
The proof of this lemma can be directly derived from Proposition 2.1,we omit it.

The multiplicity in the above lemma implies that we need to select a subspace of H such that the kernel of T restricted on it is one-dimensional. To this end,let us introduce the following three isometries

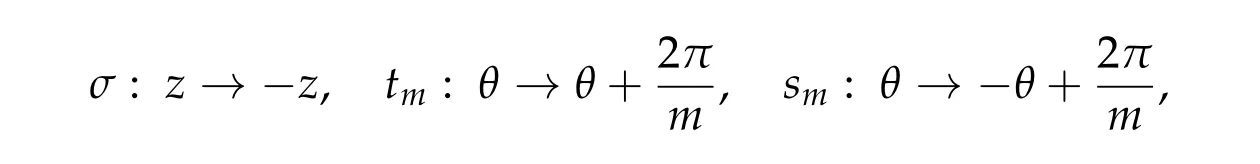
where m ＞1 is an odd integer. We also introduce the following spaces

Proof. First,we need to prove that the range of operator Tmis Ym. Laplace-Beltrami operator can be written as

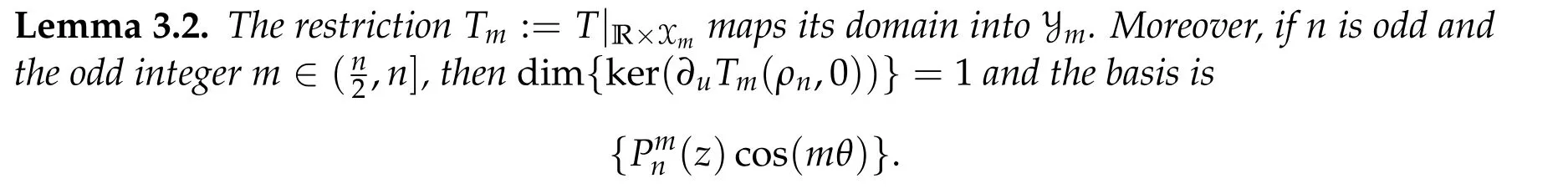
On one hand

On the other hand

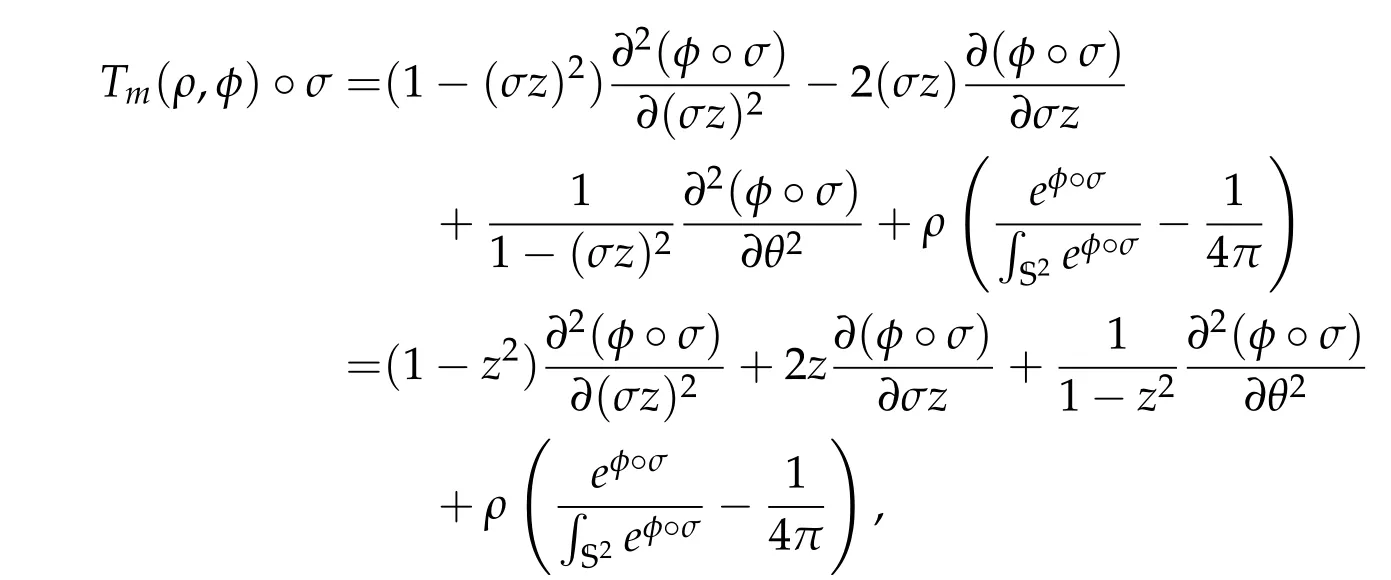
which yields Tm(ρ,u°σ) = (Tm(ρ,u))°σ. Similarly, we may prove Tm(ρ,u°tm) =(Tm(ρ,u))°tmand Tm(ρ,u°sm) = (Tm(ρ,u))°sm. Hence we know that Tm(ρ,·) maps Xmto Ym.

is a combination of the two generators of its kernel.

Of course, since Eq.(1.1)is rotationally invariant, in general this argument does not give rise to new solutions different from the previous ones.

Lemma 3.3. The range of the operator ∂uTm(ρn,0)has co-dimension one and is given by

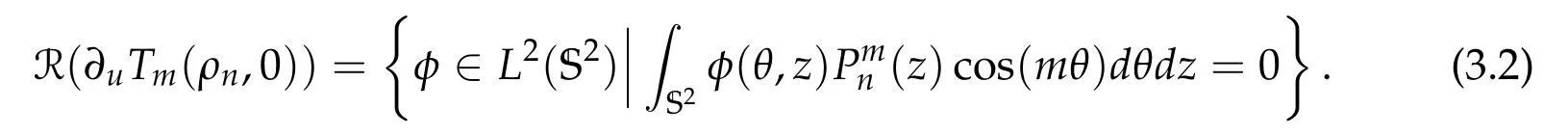
Proof. By the definition of the operator T and the well-known spectral properties of-Δgon S2, the range of ∂uTm(ρn,0) coincides with the orthogonal of its kernel. This and the result of Lemma 3.2 yield the desired results of this lemma.

Therefore,owing to

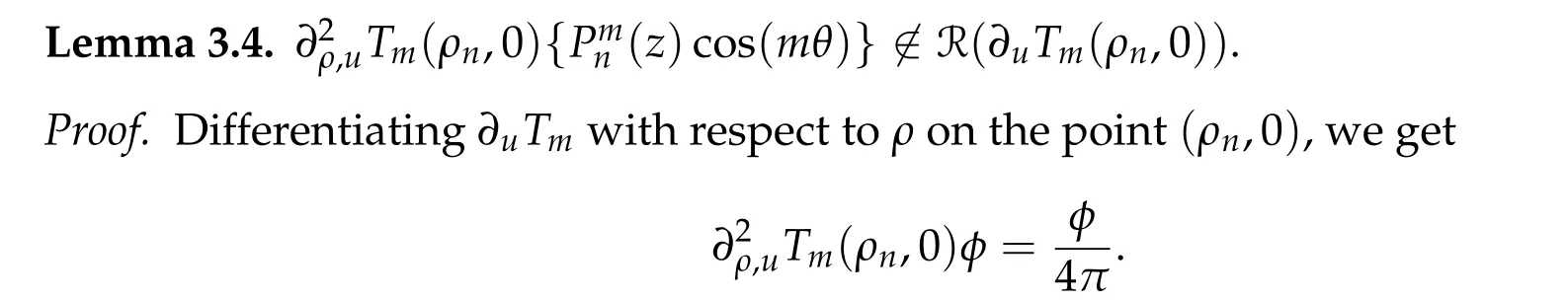
we know that

where we used the results in Lemmas 3.2 and 3.3.

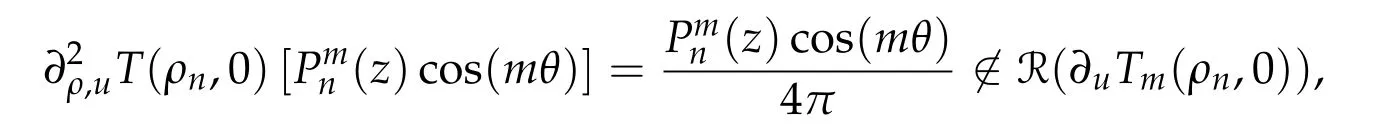
Proof of Theorem 1.1. We apply Proposition 2.2 with Tm: R×Xm→Ym. Then the existence of a local branch follows from Lemmas 3.2-3.4,namely there exists a branch of non-trivial solutions(ρn(ε),uε),where uεsatisfies

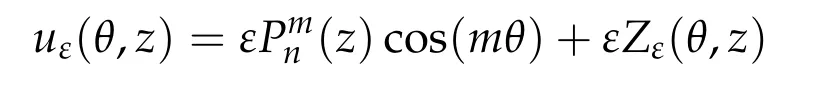
with Zεsatisfying Z0=0. Moreover,since uε∈Xm,then Zε∈Xm,so it satisfies

In order to show that the bifurcation is global we use a degree argument. We introduce operators F and G as follows

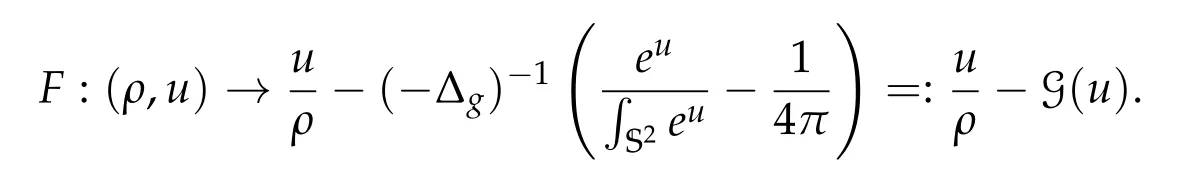
Note that F = -ρ-1(-Δg)-1T. Then it is immediate to check that Lemma 3.2 holds true for the operator F,namely 0 is the simple eigenvalue of the operator

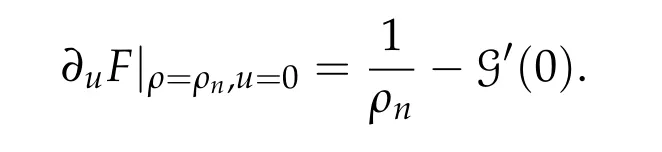
Note that the operator G is a compact operator from H to itself. Hence classical results in bifurcation theory(see[22]or[23])ensure the existence of a global continuum of solutions to(1.1)satisfying the Rabinowitz alternative,i.e.,a global continuum of solutions to(1.1)either goes to infinity or meets the trivial solution curve(ρ,0)at ρ = ρk,k /= n. We note that it is a challenging task to exclude the second possibility here.□

To prove Theorem 1.2, we need to introduce the following lemma, which is slightly different from Lemma A.3 in[2].

Lemma 3.5. For any ζ ∈R(∂uT(ρn,0)),the only solution φ ∈ker(∂uT(ρn,0))⊥of

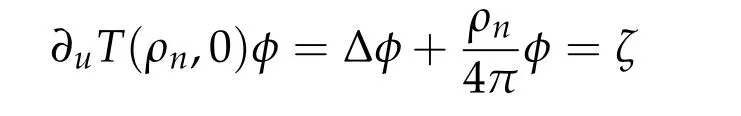
is given by

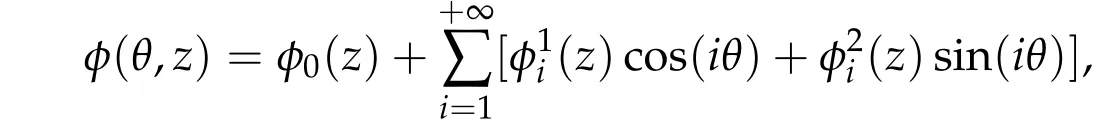
where

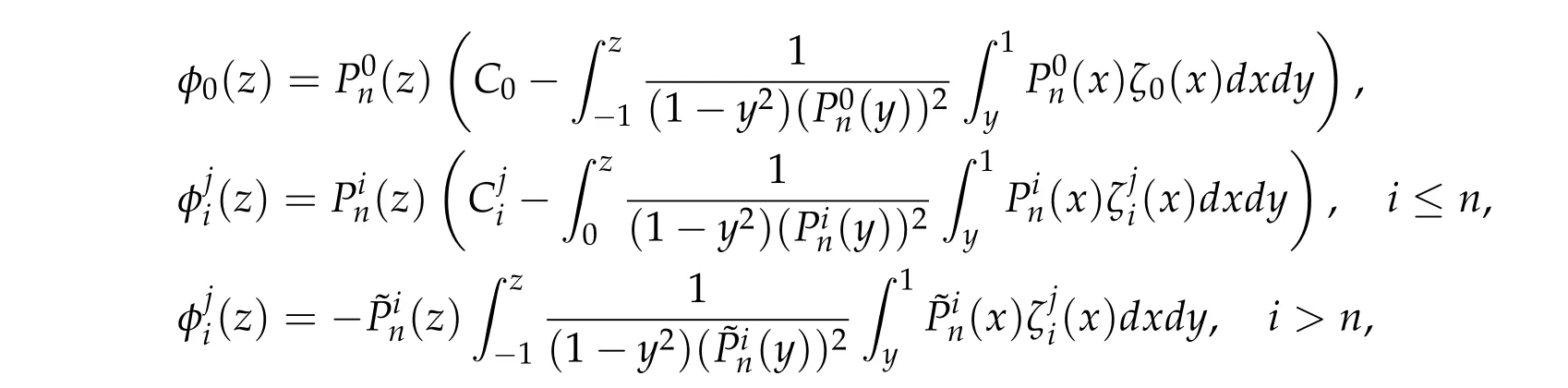
with C0,Ciuniquely determined by

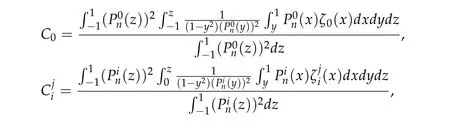
and ζ0,ζidefined by the Fourier decomposition in θ

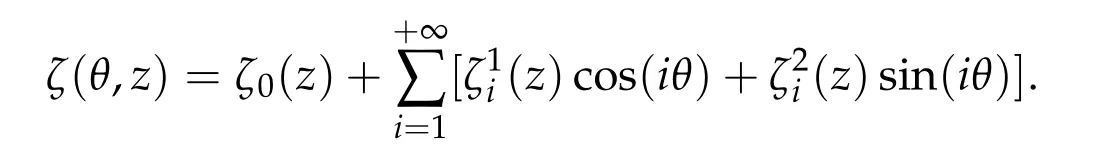
Proof of Theorem 1.2.

From Proposition 2.3 we have

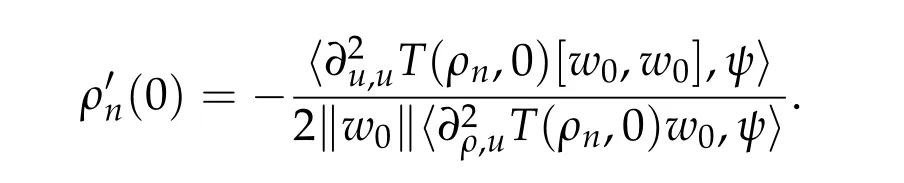
Simple computation shows that

which follows from that

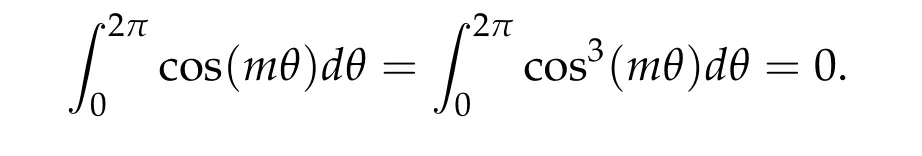
We have

It is not difficult to compute that

?

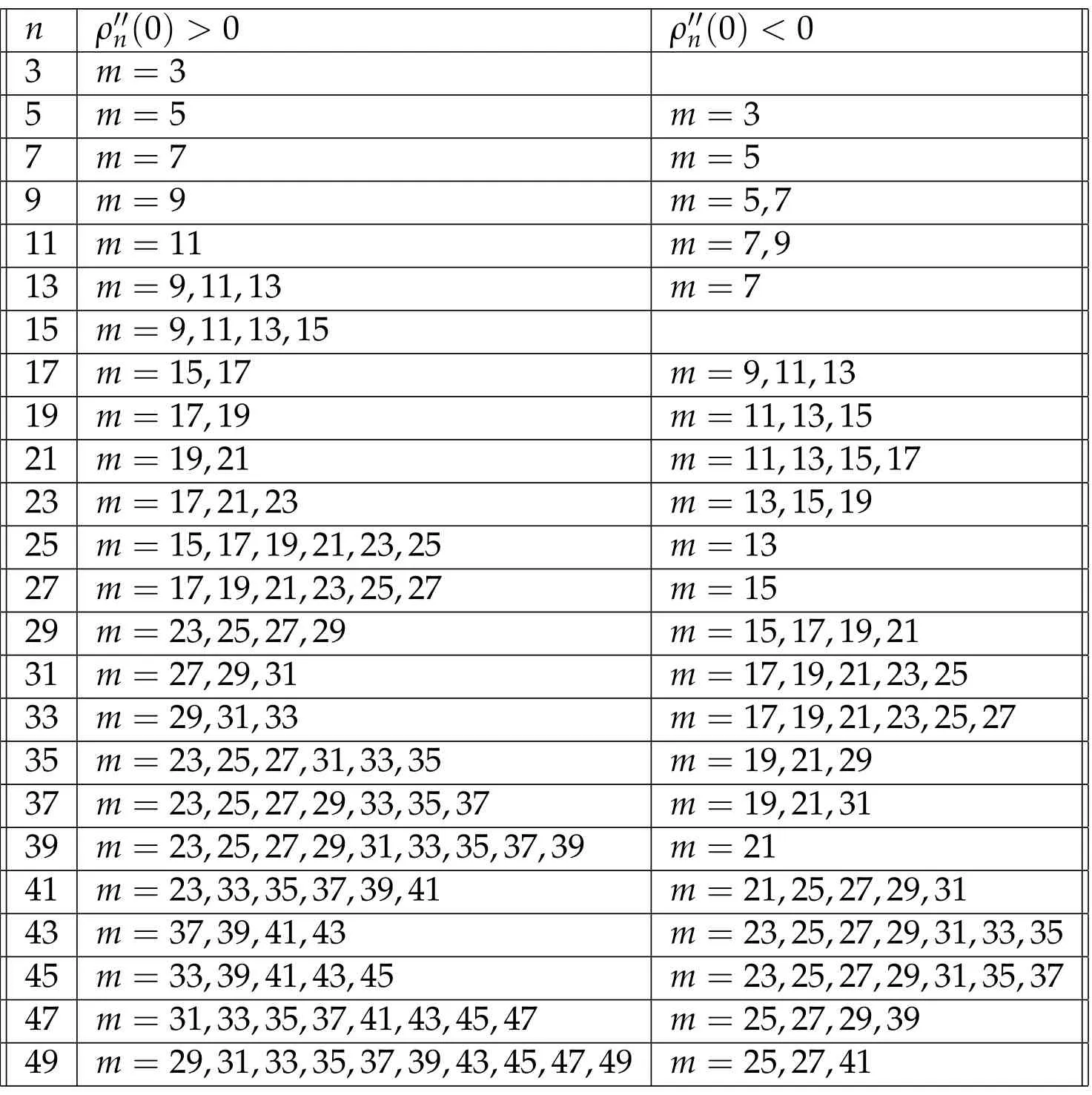
Acknowledgements

The authors would like to thank the anonymous referee for the comments which are helpful for the revision of the paper. The first author is supported by the Natural Science Foundation of Hunan Province,China(Grant No.2016JJ2018). The second author is partially supported by NSF grants DMS-1601885 and DMS-1901914 and Simons Foundation Award 617072.