基于STEM教育理念的《曲边梯形的面积》教学及启示

竺屹　袁智强

摘要：基于STEM教育理念，以“6E”教学模式为框架，融入工程问题和物理知识以及数学史，运用GeoGebra软件，设计和实施了《曲边梯形的面积》一课教学，引导学生从实际问题出發探究知识本质，从“割圆术”出发探究曲边梯形面积的计算方法，并通过技术的运用体会“以直代曲”“无限逼近”的数学思想，再利用知识迁移启发思考、拓展应用。得到的教学启示有：寻找实际问题，凸显STEM教育应用价值;重视技术应用，体现STEM教育时代特征;实现交叉融合，达成STEM教育培养目标。

关键词：STEM教育“6E”教学模式GeoGebra《曲边梯形的面积》

进入21世纪，我国的综合实力日益强盛，但核心技术受制于人的局面没有得到根本性改变。2018年1月，《国务院关于全面加强基础科学研究的若干意见》印发，指出要加强基础科学研究，促进自然科学、人文社会科学等不同学科间的交叉融合。2018年9月，《教育部等六部门关于实施基础学科拔尖学生培养计划2.0的意见》印发，要求促进学科交叉、科教融合。2020年1月，《教育部关于在部分高校开展基础学科招生改革试点工作的意见》印发，决定自2020年起，在部分高校开展基础学科招生改革试点，这就是“强基计划”。“强基计划”主要选拔培养有志于服务国家重大战略需求且综合素质优秀或基础学科拔尖的学生;聚焦高端芯片与软件、智能科技、新材料、先进制造和国家安全等关键领域以及国家人才紧缺的人文社会科学领域，由有关高校结合自身办学特色，合理安排招生专业;要突出基础学科的支撑引领作用，重点在数学、物理、化学、生物以及历史、哲学、古文字学等相关专业招生。可见，在中小学渗透以科学（Science）、技术（Technology）、工程（Engineering）和数学（Mathematics）为主的学科交叉融合教育（即STEM教育）理念变得越来越重要了。

目前，我国中小学开展STEM教育还面临着很多困难，不少学校的STEM课程是不加修改直接引自国外的。然而，我国的教学模式和国外的教学模式有着较大的差别，生搬硬套国外的教学模式未必能起到较好的效果。因此，在开发STEM课程的同时，更应该寻找国外STEM教学模式与我国分科式教学模式的“中间地带”，在常规课程（如中学数学课程）中融入跨学科的STEM教育理念，培养学生的理工科综合思维。

根据上述想法，笔者基于STEM教育理念，以“6E”教学模式为框架，融入工程问题和物理知识以及数学史，运用GeoGebra软件，设计和实施了《曲边梯形的面积》一课教学，引导学生从实际问题出发探究知识本质，从“割圆术”出发探究曲边梯形面积的计算方法，并通过技术的运用体会“以直代曲”“无限逼近”的数学思想，再利用知识迁移启发思考、拓展应用。

一、设计思路

“6E”教学模式是在“5E”教学模式的基础上修改与拓展建立的，教学过程主要包括情境引入（Engage）、科学探究（Explore）、原理解释（Explain）、数学实验（Experiment）、模型精致（Elaborate）和总结评价（Evaluate）六个环节。基于这一模式，本节课的教学分为六步：

（1）介绍大桥侧截面面积对侧面抗风能力的影响，提出实际问题，让学生对曲边梯形有一个初步的认识，激发学生的好奇心。

（2）让学生通过小组合作的方式初步探索曲边梯形面积的求解方法，培养学生的合作学习能力;然后由学生分享探究结果，培养学生的语言表达能力。

（3）通过GeoGebra软件展示“割圆术”，总结思想方法，引导学生类比归纳出曲边梯形面积的求解方法。

（4）引导学生利用GeoGebra软件求解曲边梯形的面积，感受不足近似值与过剩近似值之间的关系，力图对逼近过程有更直观的理解。

（5）引导学生利用获得的数学模型，通过GeoGebra软件解决课始提出的问题;然后介绍曲边梯形面积的求解方法在其他领域的应用，促进学生迁移知识，对定积分形成初步认识。

（6）进行总结性评价，使教师与学生分别对各自的教与学有清晰的认识，促进教学与学习能力的发展。

二、实施过程

（一）视频赏析，情境引入

教师带领学生观看视频，了解创造了四项世界纪录的湘西矮寨大桥（图1为大桥侧面照片）。

然后，用问题驱动法引入曲边梯形概念——

师如果用一个平行于桥侧面的平面去截大桥，会得到什么样的平面图形呢？哪位同学能上台把图形画在黑板上？

（一位学生上台在黑板上画出图2。）

师非常好！这就是我们今天要学习的曲边梯形。（出示图3）把这个图形放到平面直角坐标系中，就可以得到曲边梯形的解析定义：由直线x=a、x=b（a≠b）、y=0和曲线y=f（x）所围成的图形。

接着，提出求曲边梯形面积的实际问题——

已知悬索桥侧截面的上边界是抛物线，由于侧截面面积对侧面抗风能力有一定的影响，所以，工程师需要算出大桥的侧截面面积。湘西矮寨大桥全长1176米，高度330米，悬索最低点与桥面的距离为2米，你能帮助工程师算出矮寨大桥的侧截面面积吗？

（二）小组合作，科学探究

学生以小组为单位合作探究如何计算矮寨大桥的侧截面面积。小组讨论后，全班分享各组的方法——

生（出示图4）可以连接曲边梯形的两个上端点，用梯形的面积代替曲边梯形的面积。

师这位同学想到了用梯形的面积来代替曲边梯形的面积，可是误差是不是有些大了？其他同学有没有能使误差更小的方法？

生（出示图5）我们认为，可以将整体面积分为一个矩形和另一个特殊的曲边梯形（曲边三角形）。矩形的面积可以求出，但是特殊曲边梯形面积的求解有些困难，我们还无从下手。

师这位同学将面积分为了两部分，其中一部分容易求解，另一部分较难求解。

生老师，我们有好方法。（出示图6）我们可以先将曲边梯形一分为二，再用梯形来代替每一个小曲边梯形，这样就可以减小误差了。如果分得更细，则误差会更小。

师这位同学为我们提供了非常好的思路。我们可以先分割，再近似代替，这样就可以减小误差了。

（三）历史介绍，原理解释

教师引领学生走进历史，回顾古人的思想方法——

师其实，这位同学的思路和我国魏晋时期的数学家刘徽的思想如出一辙。哪位同学还记得刘徽计算的是哪种图形的面积？

生圆。

师他使用的是什么方法？

生（迟疑）割圆术。

师没错，我国古代数学家刘徽用“割圆术”求出了圆的面积。

然后，带领学生回顾“割圆术”的步骤：（1）将圆等分成n个小扇形;（2）用小三角形的面积近似代替小扇形的面积;（3）求小三角形的面积之和（即正多边形的面积）;（4）随着n的不断增大，正多边形的面积不断逼近圆的面积。其中，用圆内接正n边形的面积代替圆的面积，称作“不足近似值”;用圆外切正n边形的面积代替圆的面积，称作“过剩近似值”。

接着，用GeoGebra软件演示“割圆术”中随着n的增大，圆内接和外切正n边形面积逐渐逼近圆面积的过程（如图7）。

最后，引导学生总结出刘徽的“割圆术”体现的“以直代曲”“无限逼近”的数学思想后，利用这一思想，从特殊的情况出发，探究直线x=0、x=1、y=0和抛物线y=x2所围成的曲边梯形的面积的求法——

1.分割。

师采用什么方式分割？

生可以在x轴上将[0，1]等分为n个小区间。

生也可以在y轴上将[0，1]等分为n个小区间。

师非常好！我们不妨以x轴为例来分割。（出示下页图8）分割后的n个小区间分别是——

师你发现了什么？

生两种近似值的极限相同。

师这就说明了，无论采用小矩形、大矩形还是梯形来近似代替曲边梯形，最终得出的面积都是一样的。通过上述方法，我们得到了曲边梯形的面积。这一方法的核心是四个步骤：分割、近似代替、求和、取极限。

（四）技术整合，数学实验

教师引导学生利用GeoGebra软件，体会动态逼近的过程，验证上述结论的正确性——

首先，在指令栏中输入“x^2”，并设置页面属性使绘图区只显示函数自变量取值在0—1的部分。

然后，点击“滑动条”，并在绘图区单击创建滑动条，在弹出的对话框中设置名称为“a”，类型为“整数”，区间为1到500，增量为1。

接着，在指令栏中输入求下和（不足近似值）指令“Lower Sum（f，0，1，a）”。拖动滑动条逐渐增加a的取值，记录下不足近似值随矩形个数增加的变化趋势（如表1）。

最后，在代数区隐藏不足近似值，并在指令栏中输入求上和（过剩近似值）指令“Upper Sum（f，0，1，a）”。拖动滑动条逐渐增加a的取值，记录下过剩近似值随矩形个数增加的变化趋势（如表2）。

（五）迁移启思，模型精致

教师对“分割—近似代替—求和—取极限”的模型加以拓展，指出此模型是求不规则图形面积的一般方法。

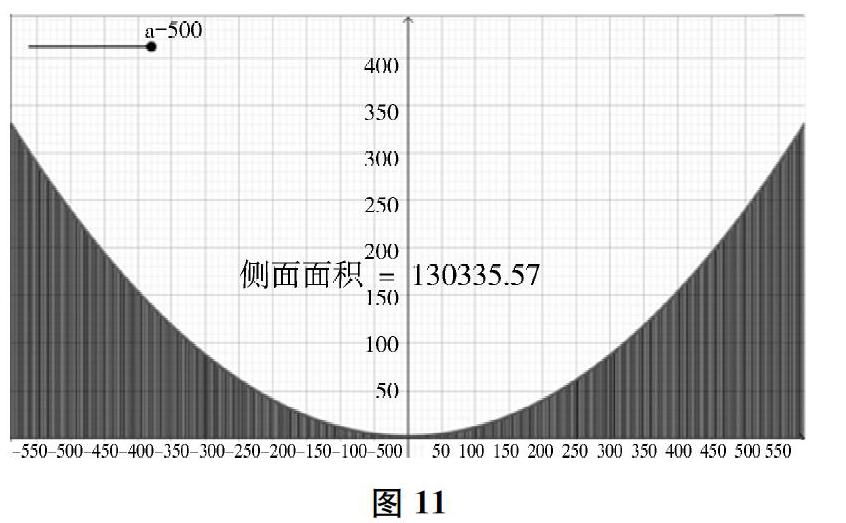
然后，回到课始的实际问题，请学生运用这一方法，利用GeoGebra软件，计算矮寨大桥的侧截面面积：首先，以桥中心为原点建立直角坐标系，由已知条件可以求出矮寨大桥悬索上边界的函数表达式为y=0.00095x2+2;其次，在GeoGebra软件中，运用不足近似值计算得到矮寨大桥的侧截面面积约为130335.57平方米（如图11）。

接着，引导学生思考计算曲边梯形面积的数学模型在其他领域的应用——

师大家现在都知道了计算曲边梯形面积的方法，那么，这种方法还可以运用在哪些实际问题中呢？

生可以计算变速运动中的位移，只需要画出vt图。

生还可以求变力做功。

师非常好！那老师就给大家布置一道课后作业题。

（出示作业题：某汽车在道路上直线行驶，前8秒钟的vt图如图12所示，已知两段曲线都为抛物线，求在这8秒中汽车开了多远？答案保留整数。）

师其实，农业生产中常用的土地面积测量仪也是以计算曲边梯形面积的方法为原理进行工作的。而且，牛顿和莱布尼兹利用计算曲边梯形面积的思想方法创立了微积分，极大地推动了数学的发展，也推动了力学、工程等学科的发展。

（六）自我反思，总结评价

教师带领学生回顾本节课学习的主要内容，并且再次归纳求曲边梯形面积的四个步骤：（1）分割——化整为零;（2）近似代替——以直代曲;（3）求和——积零为整;（4）取极限——无限逼近。同时，再次明确其中蕴含的重要数学思想就是“以直代曲”“无限逼近”。

最后，教师与学生对整个探究过程的各个环节提出修改意见，并对各个环节表现比较好的小组给予积极的评价——当然，评价贯穿于整节课，即在每个环节都给出阶段性评价，最后再给出总结性评价。

三、教学启示

（一）寻找实际问题，凸显STEM教育应用价值

本节课的教学由实际的工程情境引入，并将数学知识迁移运用到物理领域的位移计算和生活中的土地测量中，可以有效引导学生认识数学在科学技术和社会发展中的作用，感悟数学的价值，提升学生的科学精神、人文素养和应用意识。要自然地将STEM教育的理念融入常规课堂，还需尽可能地挖掘各种素材，将工程、科学与数学知识融为一体，在实际问题的解决中培养学生的数学建模素养，凸显STEM教育的应用价值。

（二）重视技术应用，体现STEM教育时代特征

通过本课例不难看出，GeoGebra等软件能帮助学生感受无限分割与无限逼近的动态过程，使数学知识达到“可视化”的效果。也就是说，教育技术深入到学科中可以帮助学生更加深刻地理解学科内涵。在当今“互联网+”时代，信息化教学技能是教师必须掌握的核心技能之一。学校应当以教育技术培训为依托，培养教师实施信息技术与学科教学深度融合的信息化教学能力。在教学设计中，教师要以信息技术支持的跨学科教育为切入点，培养学生的创新精神和实践能力，体现STEM教育的时代特征。

（三）实现交叉融合，达成STEM教育培养目标

学科交叉融合已经成为科技和教育发展的重要趋势。STEM教育能够为学生提供充分的机会，有效地发展多元的思维方式。因此，学校和教师应当正确认识STEM教育的内涵与意义，结合我国国情，寻找数学与工程、科學知识的整合点，系统地进行课程开发与研究;在教学设计中，既保留传统教学内容，又结合科学与工程知识，并且运用信息技术，搭建起各学科之间的桥梁，实现多学科的交叉融合;同时，着力建设STEM教育的评价体系，从而达成STEM教育的培养目标——通过跨学科的教学培养具备理工科综合思维的创新型人才。

参考文献：

[1] 袁智强.交叉融合的STEM教育：背景、内涵与展望[J].教育研究与评论（中学教育教学），2019（3）.

[2] 王诗瑶，王永红.跨学科STEM教育的思辨、现状与应用[J].教学与管理，2018（33）.

[3] 梅浩，袁智强，郑柯.基于数学实验的STEM教育——以“探究金属的冷却模型”为例[J].教育研究与评论（中学教育教学），2019（3）.

[4] 张景中，葛强，彭翕成.教育技术研究要深入学科[J].电化教育研究，2010（2）.