近场动力学框架下的键基对应模型
陈 壮,万 冀,楚锡华*,2
(1.武汉大学 土木建筑工程学院,武汉 430072;2.大连理工大学 工业装备结构分析国家重点实验室,大连 116023)
1 引 言
近场动力学PD(Peridynamics)是一种基于非局部思想对传统连续介质理论进行重构的物理模型,最早由Silling提出[1]。该方法将微分形式的平衡方程用积分形式进行改写,使得平衡方程在裂纹等空间不连续处也可以成立。根据PD理论建立的数值模型可以有效地模拟动态裂纹的扩展现象。裂纹的产生、发展和分叉等现象在模拟时都不需要外部判断条件。目前,PD由于其模拟动态破坏现象的能力,受到研究者们的关注[2-4]。
PD理论目前主要分为键基PD(bond-based PD)[1]和态基PD(state-based PD)[5]两种,键基PD的局部相互作用机制比较简单,可以模拟裂纹的动态扩展现象,但是键基PD存在泊松比限制问题(三维及平面应变问题,泊松比μ=1/4;平面应力问题,泊松比μ=1/3),无法区分体积变形和偏变形,这给键基PD的应用带来了一定的限制。态基PD是一种更加一般的PD模型,分为常规态(ordinary state-based PD)和非常规态(non-ordinary state-based PD)两种,键基PD是态基模型的一种特例。态基PD虽然没有泊松比取值的问题,但是基于态基PD发展的数值模型比键基PD要复杂,计算规模较大。此外,非常规态基PD中物质点的变形也存在零能模式的问题[6]。许多学者采用修正键基PD的方式解决泊松比限制的问题。Gerstle等[7]提出了微极PD模型,在键基PD中引入新的微观弹性常数,使得键基PD独立的微观材料参数在各向同性线弹性体中变成两个;Zhu等[8]提出了考虑键转角的键基PD模型,该模型可以很好地模拟泊松比取其他值时材料的力学行为;Zhou等[9]提出了考虑键间转角的共轭键线弹性模型,并且修正了键断裂的模型;Hu等[10]考虑键的法向和切向作用,从而解决了键的泊松比限制。
本文提出了一种键基对应PD模型,通过定义单根键的变形梯度来计算应变,进而计算应力和物质点间的近场力。键变形梯度的定义在小变形与键长趋近无穷小时可以退化为经典的变形梯度张量。在键对应PD模型中不需要对PD微观弹性常数进行计算,直接采用物理方程求应力以及近场力。数值算例模拟了准静态平板受拉和Kalthoff-Winkler板冲击试验。平板受拉算例对比键基对应PD和传统键基PD的结果,验证了键基对应PD在解决泊松比限制的有效性;对Kalthoff-Winkler板冲击试验的数值模拟,验证了键基对应PD在模拟动态裂纹扩展上的有效性。
2 近场动力学简介
考虑占据一定空间Ω的物体B,B中某一点x受到周围一定区域Hx内点x′的作用,如图1所示,根据牛顿第二定律,得到PD的动力学方程为
(1)
键基PD中定义键的伸长率s为
s=(‖ξ+η‖-‖ξ‖)/‖ξ‖
(2)
式中ξ=x′-x为相对位置,η=u′-u表示相对位移。
在键基PD中,通过键传递的近场力f的大小和伸长率成正比,方向沿着键的方向:
(3)
c为PD微观弹性参数,通过对比键基PD的应变能密度和传统连续介质力学的应变能密度得到[11]
c=18κ/πδ4
(4)
式中κ为体积模量,δ为近场范围尺寸,关于c取值的相关讨论可以参考文献[12]。
键基PD模拟各向同性线弹性的材料时,独立的材料参数只有一个,这和传统理论中各向同性线弹性体应该有两个独立的材料参数有差别,而且键基PD无法区分体积变形和偏变形,这些问题导致了键基PD只能正确模拟泊松比取限制值的材料。
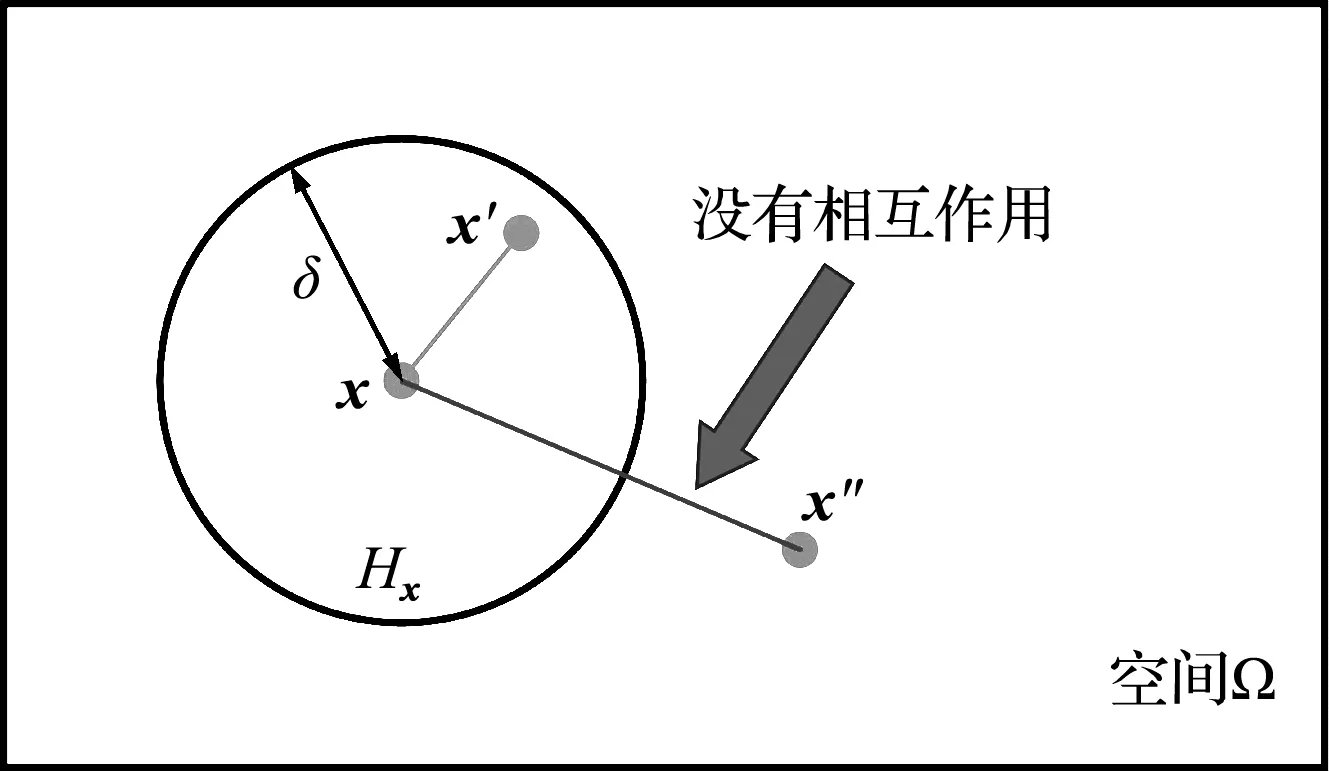
图1 PD中物质点的非局部相互作用
Fig.1 Interaction of material points
(5)
在键基PD中,s0的取值和极限能量释放率Gc、键基PD微观弹性参数c以及近场范围尺寸δ有关
(6)
(7)
损伤值越大,表明连接点x的键断裂的数目越多,点x附近的损伤越严重。
3 键变形定义
fx x′=RU
(8)
在二维问题中
(9)
(10)
在三维问题中,为简化表述只画出Δα的变化情况,其余两个平面类似,如图3所示。
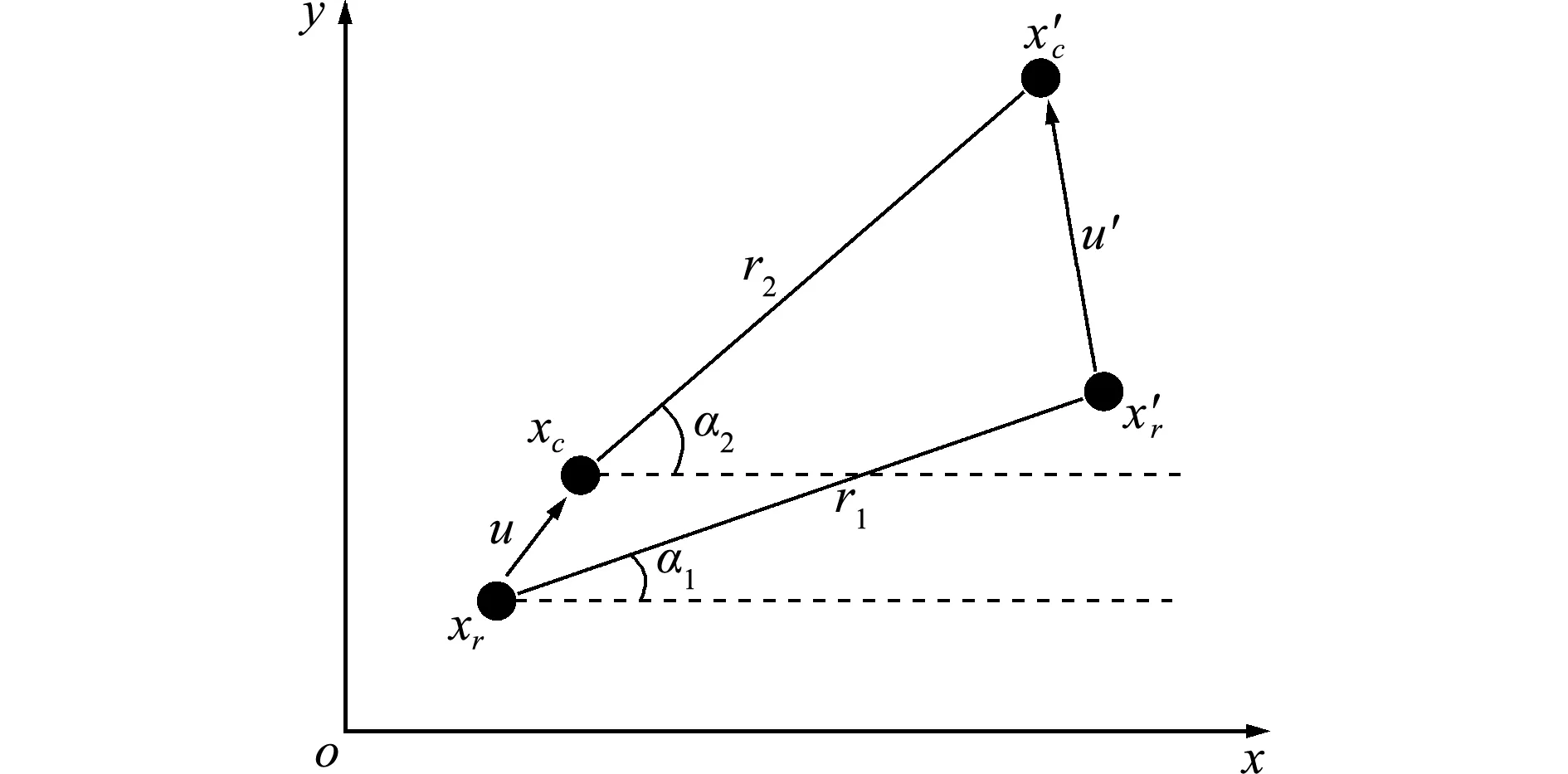
图2 二维情况下键变形的定义
Fig.2 Deformation of bond in 2D problems
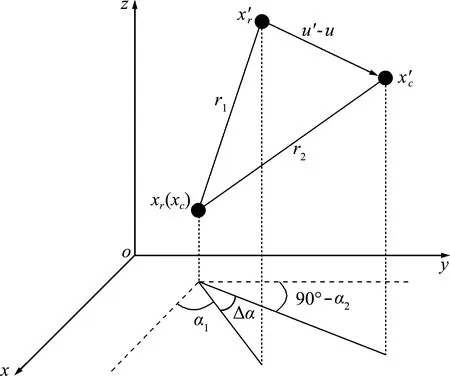
图3 三维情况下键角度变化在x-y平面的投影
Fig.3 Bond’s projection onx,yplane
(11,12)
R各分量具体是
R11=cos(Δβ)cos(Δθ)
(13a)
R12=cos(Δβ)sin(Δθ)
(13b)
R13=-sin(Δβ)
(13c)
R21=-cos(Δα)sin(Δθ)+
sin(Δα)sin(Δβ)cos(Δθ)
(13d)
R22=-cos(Δα)cos(Δθ)+
sin(Δα)sin(Δβ)sin(Δθ)
(13e)
R23=sin(Δα)cos(Δβ)
(13f)
R31=sin(Δα)sin(Δθ)+
cos(Δα)sin(Δβ)cos(Δθ)
(13g)
R32=-sin(Δα)cos(Δθ)+
cos(Δα)sin(Δβ)sin(Δθ)
(13h)
R33=cos(Δα)cos(Δβ)
(13i)
(14)
式中R为键的刚体转动,U为键的伸长,r1为变形前的键长,r2是变形后的键长,假设垂直于键方向没有发生变形。fx x′反映了键在局部坐标系下的变形情况,这种变形定义的合理性证明如下。
设物体受到外力作用后产生的变形张量场为F0(x,y,z),对于该物体内部任意一条键lM N,点的坐标M(x1,y1,z1)和N(x2,y2,z2),在小变形假设下有R≈I,I为单位矩阵,键lM N的变形根据式(8)计算:
(15)
假设键的长度极小,点M和N无限接近,键lM N的局部变形张量F0(x1,y1,z1)≈F0(x2,y2,z2),实际上键lM N在小变形以及键长无限小的情况下就等同于过点M或N的线元。根据变形张量的定义,在局部坐标下,键lM N的变形张量为
(16)
可以发现,在键长趋近无穷小以及小变形的情况下,键的变形张量定义和经典连续介质力学中变形张量的定义是一致的。
接下来通过键的变形张量计算应变和应力,在应力的基础上计算近场力。首先进行坐标转换,将局部坐标系转换到全局坐标系中,T为坐标转换矩阵,
(17)
计算位移梯度张量
(18)
在小应变下的应变定义为
(19)
线弹性条件下的应力
σx x′=Dεx x′
(20)
定义局部作用面积Sx x′来描述通过键传递应力的作用面积,Sx x′的取值和网格划分的尺寸Δx有关,本文取Sx x′=(Δx)2为物质点的截面积。根据键传递应力来计算近场力,考虑到键长和物质点体积对近场力作用的影响,引入影响函数ω=ω(ξ,Vx′),其中ξ为点x和x′的相对位置矢量,Vx′为点x′的体积,本文忽略距离的影响,只考虑物质点体积的影响
ω(ξ,Vx′)=Vx′/VH
(21)
式中VH为近场域的体积。
通过键传递应力计算近场力
(22)
式中nx x′为键的方向,
nx x′=ξ/‖ξ‖
(23)
将式(22)代入式(1)
(24)
采用了这种近场力计算方法的PD模型称为键基对应PD,在键基对应PD中,不需要计算传统键基PD的微观材料常数,直接利用物理方程求应力,进而计算近场力。
4 数值算例
4.1 准静态平板拉伸
考虑受到单轴拉伸的正方形板,如图4所示,板边长为7 m,厚度为0.175 m,上下边界加上固定位移ub=0.001 m,材料参数列入表1。采用显式积分算法计算方程(24),根据文献[11]计算临界的时间步长为Δtc=8.1×10-5s,考虑加入的人工阻尼项对计算的影响,取小于限制值的时间步长为Δt=1×10-7s。
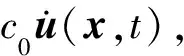
对比键基PD和键基对应PD的计算结果,y向位移和x向位移分布如图5所示。两种PD模型计算的y方向位移分布均匀,但是x方向位移受到边界效应的影响,存在一定的误差。考虑到键基泊松比限制的问题,将键基PD和键基对应PD在y=-0.4375 m的x方向位移与理论解(u*=-νεyx,εy是施加边界荷载后y方向产生的应变,ν为泊松比)进行对比,如图6所示,相对误差计算公式为‖uP D-u*‖/‖u*‖×100%。可以看出,键基对应PD比键基PD更接近于理论解,验证了键基对应PD解决泊松比限制问题的有效性。
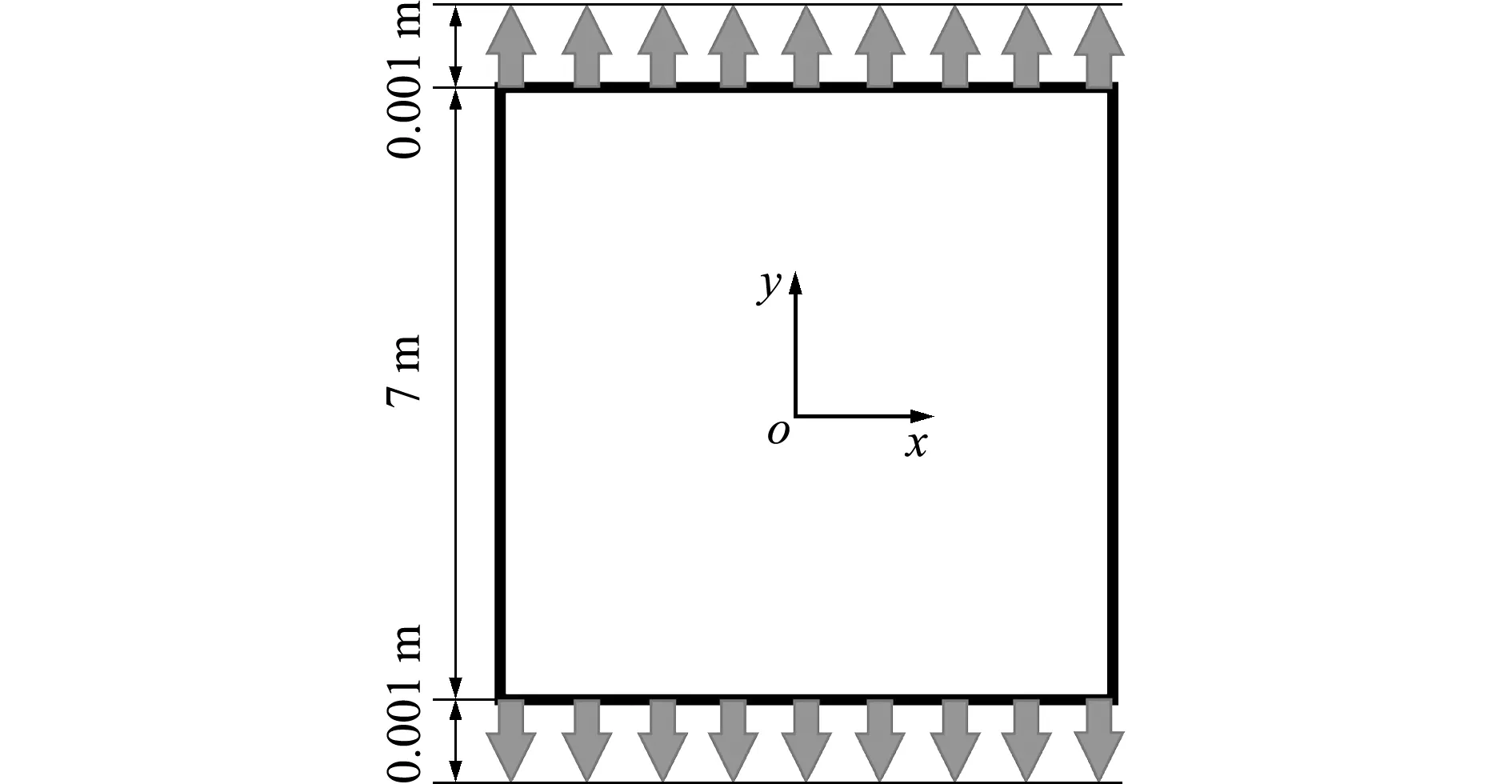
图4 平板拉伸
Fig.4 Geometry and boundary conditions of the plate
表1 平板拉伸计算参数
Tab.1 Mechanical parameters
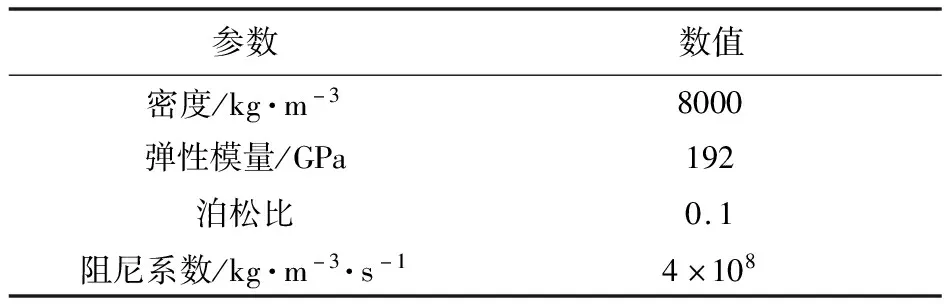
参数数值密度/kg·m-38000弹性模量/GPa192泊松比0.1阻尼系数/kg·m-3·s-14×108

图5 平板拉伸位移分布云图(单位:m)
Fig.5 Displacements of bond-based PD and bond-based corresponding PD(unit:m)
4.2 Kalthoff-Winkler板冲击试验
为验证键基对应PD模拟动态裂纹扩展的能力,进行Kalthoff-Winkler板冲击试验的数值模拟[13],考虑到原试验冲击块形状对平板动态裂纹扩展影响较小,将问题简化为二维,计算模型尺寸如 图7 所示。根据文献[14],采用对称化建模,提高计算效率。材料参数和计算参数列入表2,网格划分尺寸Δx=0.001 m,近场范围尺寸δ=3.015Δx。PD断裂准则采用键断裂准则,模拟板受冲击作用发生脆性破坏的现象。
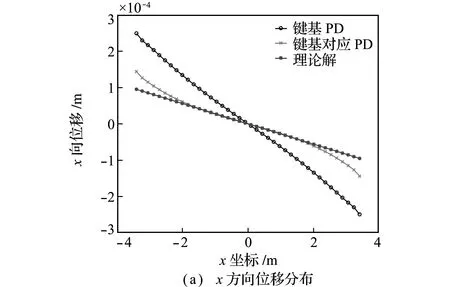
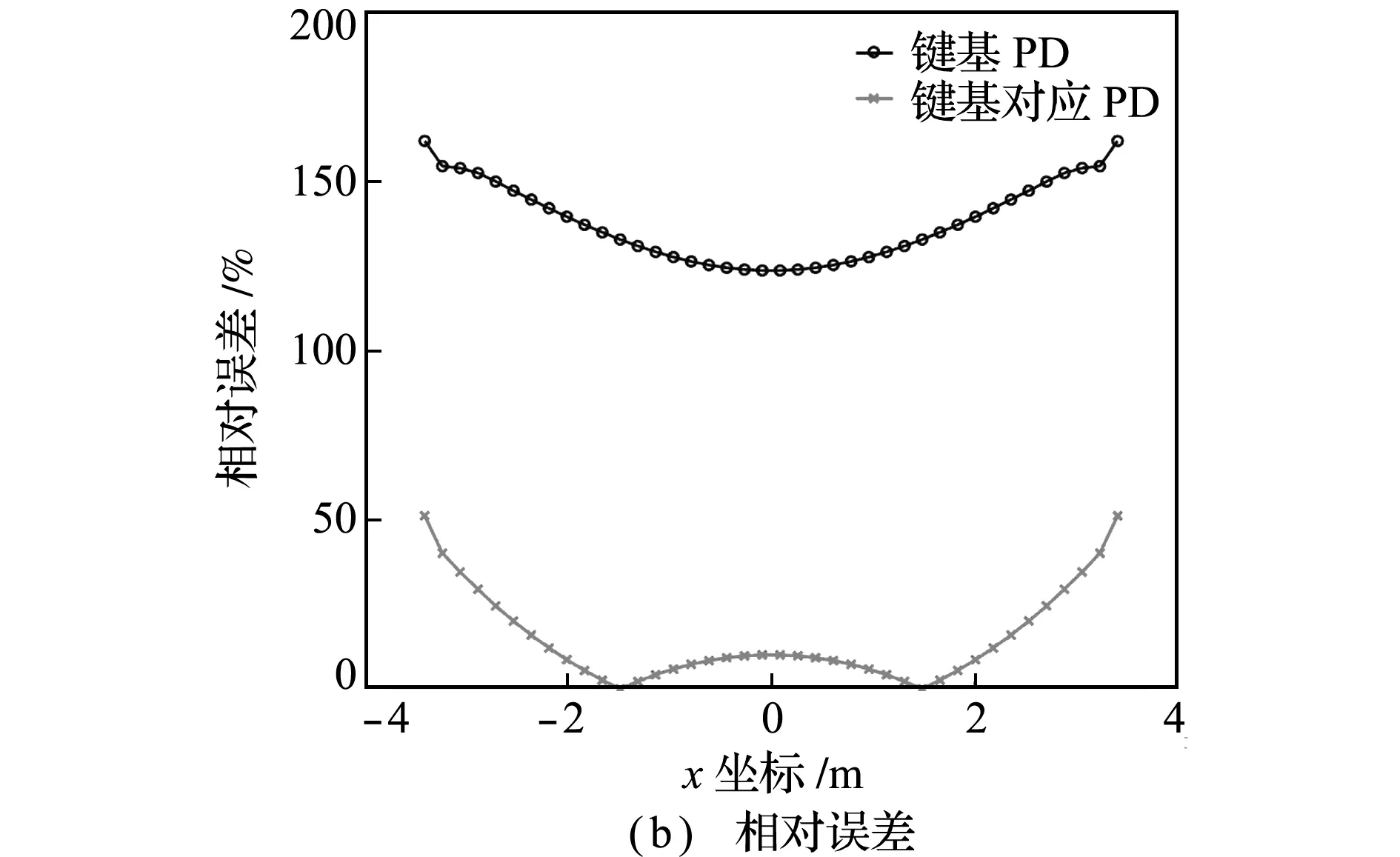
图6 键基PD与键基对应PD沿着y=-0.4375 m上x方向位移分布与理论解的对比
Fig.6xdisplacements alongy=-0.4375 m and comparison with the theoretical solution
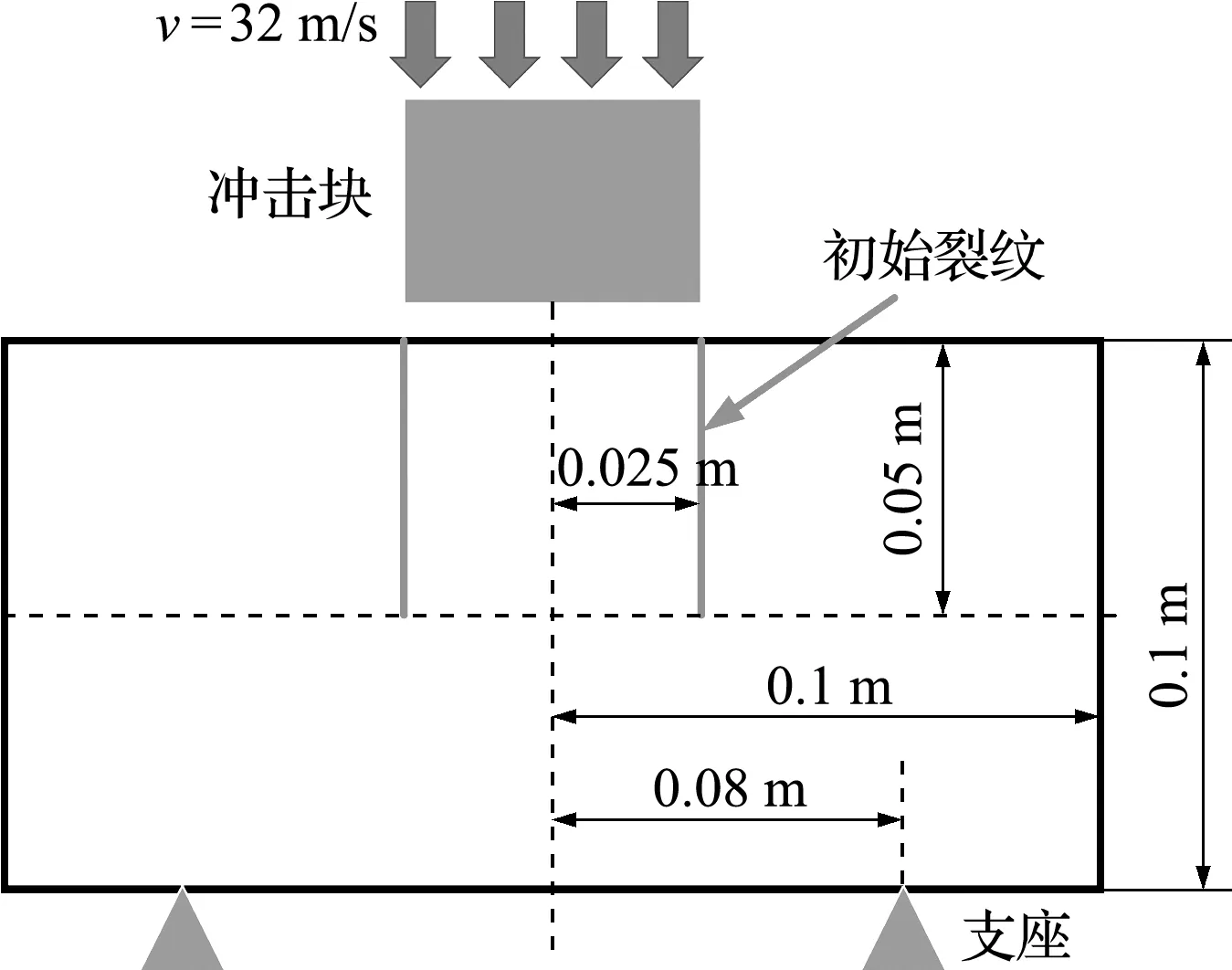
图7 Kalthoff-Winkler板冲击试验建模
Fig.7 Geometric condition of the Kalthoff-Winkler plate
裂纹扩展的模拟结果如图8所示,裂纹在初始裂纹尖端附近开始扩展,之后裂纹会先沿着与荷载呈41°夹角的方向进行扩展,随后沿着与荷载呈67°夹角的方向进行扩展,同时有裂纹分叉的现象出现。这与已有的数值模拟结果[14,16](70°)以及实验结果[15](70°)比较接近。随着荷载向下传递,损伤开始在梁的下端产生,之后向着预制裂纹所在的方向发展,这和文献[14]的现象一致。
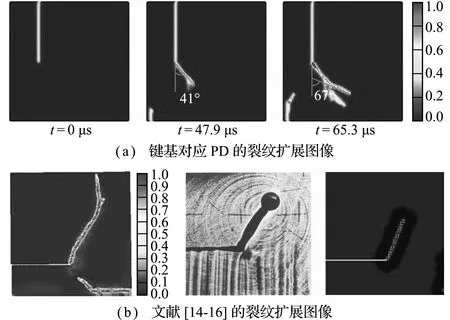
图8 Kalthoff-Winkler板冲击试验裂纹扩展随时间变化
Fig.8 Crack path of Kalthoff-Winkler plate
5 结 论
本文结合键基PD和态基PD的优点,提出了键基PD对应模型,解决了键基PD泊松比限制的问题。新的键张量变形张量在小变形以及键长趋近无限小的条件下可以退化为经典的变形张量。在此基础上利用物理方程计算应力,再通过应力来计算近场力,建立了经典连续介质力学与键基PD的联系。数值算例验证了当泊松比不取限制值时,键基对应PD相对于传统键基PD在预测平板x方向位移的正确性。对Kalthoff-Winkler板冲击试验的模拟验证了键基对应PD模拟动态裂纹扩展的有效性。
键基对应模型相比于传统键基模型,计算成本稍高,对于三维问题中对键变形梯度的描述本文也只给出了公式而没有作进一步的讨论,同时对于键变形的定义与传统变形梯度定义之间的关系还有待进一步的理论证明。

