振型归一化对梁结构柔度曲率损伤指标的影响

唐盛华, 罗承芳, 方 志, 张学兵, 楚加庆

(1.湘潭大学 土木工程与力学学院 工程结构动力学与可靠性分析湖南省高等学校重点实验室，湘潭 411105；2.湖南大学 土木工程学院，长沙 410082)

1 引 言

至2017年末，我国公路桥梁总数已达 83.25万座。由于桥梁交通量增长、材料自身性能退化以及外界复杂环境、地质灾害和疲劳等因素共同作用，为防止在役桥梁突发安全事故，降低维修成本，延长使用寿命，有必要获得准确、实时的结构状态信息，因此桥梁结构健康监测备受关注[1-3]。

结构损伤识别是健康监测的重要内容之一，近30年来，基于动力特性的损伤检测方法有了重大发展，如频率、振型和柔度矩阵等，其优势在于仅需使用相对较少的传感器测试且不影响桥梁的正常使用[4,5]。其中，由低阶频率和振型得到的柔度动力指纹指标，对结构损伤具有较高的敏感性，故基于动力参数的柔度矩阵广泛应用于结构损伤识别。文献[6,7]利用柔度矩阵得到均匀荷载面ULS(the uniform load surface)和ULS曲率,ULS对截断效应影响较小且试验误差敏感性小。唐小兵等[8]利用损伤结构的柔度矩阵各列最大值元素一次差分得到柔度曲率法指标。Wu等[9]将ULS曲率用于板结构进行损伤检测和定量，ULS曲率由切比雪夫多项式逼近法求得。曹晖等[10]提出柔度曲率差指标，对判定结构的损伤位置效果较好。Wang等[11]在ULS基础上提出广义分形维数和简化间隙平滑两种方法，用于碳/环氧复合材料梁的损伤检测。李永梅等[12]对结构柔度矩阵行列差分，取每列绝对最大值或对角元素作为损伤指标检测结构损伤。Sung等[13]提出归一化ULS曲率损伤识别方法，数值研究表明该方法优于ULS曲率法和振型曲率法。Liu等[14]提出一种损伤区域模态频率改变率和ULS曲率差，结合FCM-PSO算法两阶段损伤识别方法，能有效识别异形桥梁的损伤。唐盛华等[15]提出适用于连续梁的改进ULS曲率指标。

由于柔度类损伤识别方法的模态振型均需质量矩阵归一化，而对于实际土木工程结构，由于结构尺寸、刚度和质量巨大，难以施加人为可控激励，一般采用环境激励法进行模态测试[3,16]，无法实测出结构的质量归一化振型，使得柔度曲率类损伤识别方法在实际工程中的应用受到限制，故利用环境激励下的模态数据进行柔度曲率类损伤识别是一个重要的研究方向。针对此问题，Duan等[17,18]提出比例柔度矩阵来解决环境激励下的损伤问题，比例柔度矩阵与柔度矩阵仅相差一个比例系数，但其计算过程复杂。杨秋伟等[19，20]分别通过环境激励下检测损伤的灵敏度方法和广义柔度扰动方程结合矩阵拉直和广义逆技术，均可求出振型归一化系数。林贤坤等[21]探讨了基于附加质量的试验模态振型质量归一化方法，可实现各阶试验模态振型较高精度的质量归一化。Jung等[22]根据环境激励下加速度响应获得的模态柔度矩阵，通过实验验证了归一化ULS曲率方法，结果表明该方法抗噪声能力好且灵敏度高。

综上所述，目前学者着重研究如何将环境激励的模态振型质量矩阵归一化，不同振型归一化方法对柔度曲率类指标损伤识别的影响鲜有研究报道，而且现有柔度曲率的结构损伤识别方法大多集中在损伤定位方面，不能有效地进行损伤程度识别。本文根据位移曲率与结构刚度的关系，提出利用梁结构损伤前后的ULS曲率计算结构损伤程度的方法。并针对环境激励下的振型归一化问题，提出P-范数振型归一化方法，通过ULS曲率指标讨论不同振型归一化方法对梁结构损伤识别的影响。

2 梁结构损伤识别理论

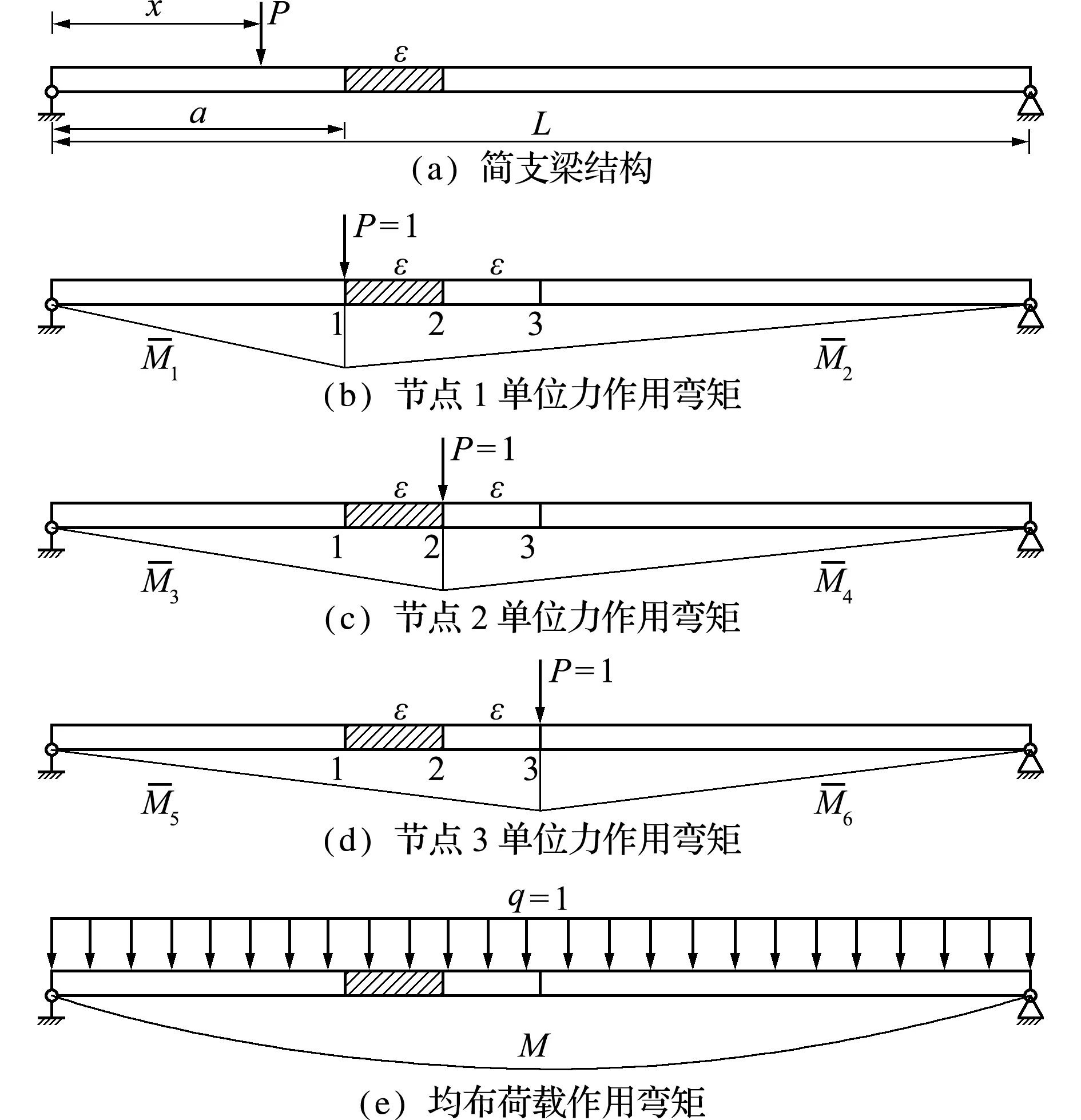
图1 简支梁结构

Fig.1 A simply-supported beam structure

(i=1,2,3)

(1)

(2)

根据结构力学可得均布荷载q=1作用下，未损伤时各节点的位移分别为

2L[a+(i-1)ε]2+L3}

(i=1,2,3)

(3)

损伤时各节点的位移分别为

(4)

(5)

(6)

式中下标u和d分别表示结构未损伤和损伤。

由中心差分法可知，节点2损伤前后的位移曲率分别为

6a2+6Lε-12aε-7ε2)

(7)

6a2+8Lε-16aε-11ε2)-

(8)

2.1 损伤定位

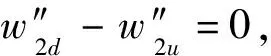
DI=[DI1DI2…DIn]

(9)

(10)

式中n为测点数目。

2.2 损伤程度定量

节点2在均布荷载q=1作用下的弯矩为

(11)

由材料力学可知，结构刚度、弯矩和位移曲率存在如下关系：

(12)

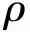
节点2损伤前后的曲率理论值为

(13)

(14)

局部损伤程度较小时，由式(8)可得

(15)

进一步计算得

(16)

联立式(13,14)可求得损伤程度为

(17)

3 振型归一化方法

由于采用环境激励获取的各阶振型振幅大小不确定，因此需要对振型进行归一化处理。除了质量矩阵振型归一化，常用的振型归一化方法还有单位矩阵振型归一化和最大绝对值振型归一化。

3.1 P-范数振型归一化

引入P-范数振型归一化的概念，对振型进行范数归一化处理，由范数定义，具体过程如下，

(18)

(19)

式中φi,n为P-范数归一化的振型，‖·‖P为向量的P-范数(P=1,2,3,…)。

特别地，当P=2时，实质上为单位矩阵振型归一化；当P=∞时，实质上为最大绝对值振型归一化。即该两种常用的振型归一化方法实则是P-范数振型归一化的两种特殊形式，因此，本文采用P-范数振型归一化进一步分析振型归一化方法对梁式结构损伤识别的影响。

3.2 振型归一化方法对损伤程度定量的影响

由频率和质量矩阵归一化的振型可以得到结构的柔度矩阵为

(20)

第i阶频率和振型计算的柔度矩阵Fi为

(21)

(22)

均布荷载作用下结构的位移曲线为ULS[6]，即将模态柔度矩阵按行(或列)加起来。第i阶柔度矩阵Fi得到的ULSi为

(23)

ULSi的第k测点曲率值采用中心差分法计算得到，

(24)

式中dl为测点k-1到测点k与测点k到测点k+1距离的平均值。

假设由某种范数归一化方法获得的实测振型为Φ=[φ1,φ2,…,φn]，结构的质量矩阵为Mr,则

(25，26)

(27)

式中αi为振型质量矩阵归一化系数。

由实测振型Φ构造的结构损伤前后第k测点的ULS曲率值分别为

(28)

(29)

根据静力平衡方程，柔度矩阵F、均匀荷载面曲率ULS ″和位移曲率w″的关系为

(30)

式中q为单位均布荷载。

将ULS ″代替式(17)的w″，故损伤程度De为

(31)

(32)

(33)

为反映损伤前后振型质量矩阵归一化系数的相对变化，定义振型质量矩阵归一化系数差为

xα=(αd 1-αu 1)/αu 1

(34)

式(32)化简为

(35)

式中无损伤时，Γr k=1；有损伤时，Γr k>1。

将式(35)代入式(31)得

(36)

由式(36)可知Γr k越大，De越大。将式(36)变形并采用泰勒公式展开：

(37)

由于损伤前后的同阶振型非常接近，即同阶的αd和αu的值接近，故xα较小。由式(37)可知损伤程度De与xα近似呈线性关系。

(38)

dDe(k)/dxα为关于Γr k的减函数，即损伤程度越大，Γr k越大，dDe(k)/dxα的变化越小，其最大值为

(39)

4 三跨连续梁算例

三跨连续梁的计算跨径为18 m+30 m+18 m，1.5 m划分一个单元，共44个单元，45个节点，材料弹性模量为E=3.25×104MPa，密度为 2550 kg/m3，泊松比υ=0.2。截面尺寸如图2所示，其中两端3 m为等截面，中间变截面梁高变化采用二次抛物线，有限元模型如图3所示。

假设损伤不引起结构质量的改变，通过弹性模量的降低来模拟单元损伤，考虑中小损伤情况，损伤工况列入表1。

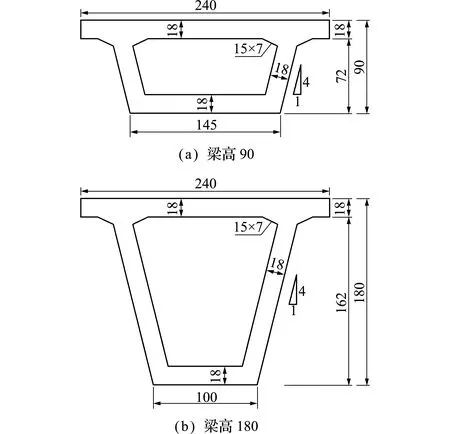
图2 箱梁截面尺寸(单位：cm)

Fig.2 Section size of box girder(unit:cm)

表1 三跨连续梁损伤工况

Tab.1 Damage cases of three span continuous beam

工况损伤单元刚度下降/%单元12单元23单元381—10—22020—3303010

图3 连续梁有限元模型(单位：cm)

Fig.3 Finite element model of a continuous beam(unit:cm)

4.1 逐跨均匀荷载面曲率差

对于多跨连续梁，采用均匀荷载q=1加载时，位移曲线将会存在拐点[15]，即存在w″=0，故相应弯矩也为0。此时，无论EI如何取值，式(12)恒成立。因此，在拐点处无法判断损伤前后结构刚度的变化，即该处无法识别其损伤。以三跨连续梁为例，均布荷载满布时有4个拐点，位置如图4所示，采用ULSC指标计算本算例工况3，结果如图5所示，单元38在拐点位置而无法识别损伤位置，损伤程度识别在4个拐点位置均有不同程度的峰值，易造成误判。

故考虑对多跨连续梁采用逐跨加载，如图6和图7所示，每种荷载情况下均只有两个拐点，并且各荷载作用下的拐点位置不同，故考虑对每跨加载后挠度曲率指标进行绝对值叠加，避免其拐点位置无法识别损伤的问题。

该指标具体实现为，对于N跨连续梁，按跨取N个均匀荷载向量，对其中任意均匀荷载qi,结构损伤前后的位移差曲率为

图4 均布荷载q作用下的结构位移

Fig.4 Structural displacement diagram under uniform distributed loadq

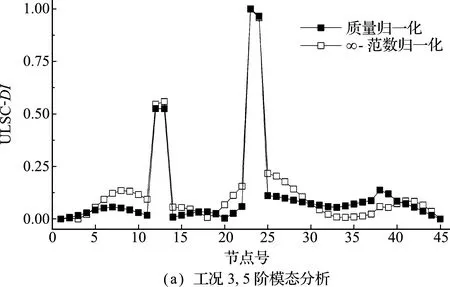
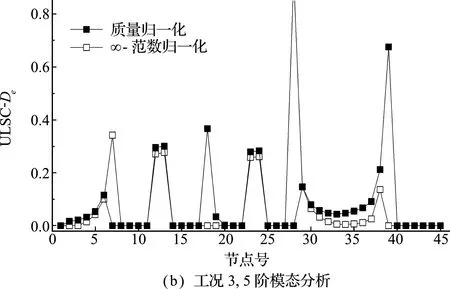
图5 指标损伤识别结果

Fig.5 Damage index identification results

(40)

最终指标取为各指标的绝对值的叠加为

(41)

故损伤程度为

(42)

4.2 损伤前后柔度矩阵差比较

以质量矩阵归一化的振型为基础，进行P-范数归一化处理，当P=0时，不作处理；当P=∞时，归一化后各阶振型的最大值均为1。因不同方法振型归一化后幅值不同，导致不同振型归一化方法计算的损伤前后的柔度矩阵差不具有可比性。为比较各振型归一化方法引起的损伤前后柔度矩阵的变化情况，对按某种范数归一化振型得到的柔度矩阵差dFP乘以一个待定系数ζ,通过ζ的调整，使ζdFP与dF0具有可比性，待定系数ζ通过式(43，44)进行求解。

min.‖ζdFP-dF0‖f ro

(43)

(44)

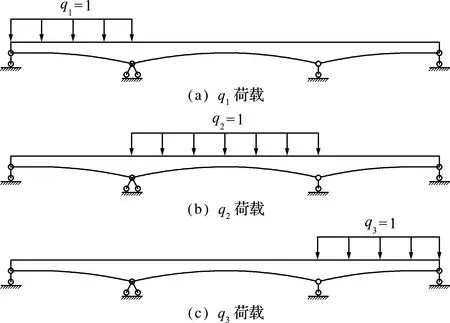
图6 均布荷载qi

Fig.6 Uniform distributed loadqi

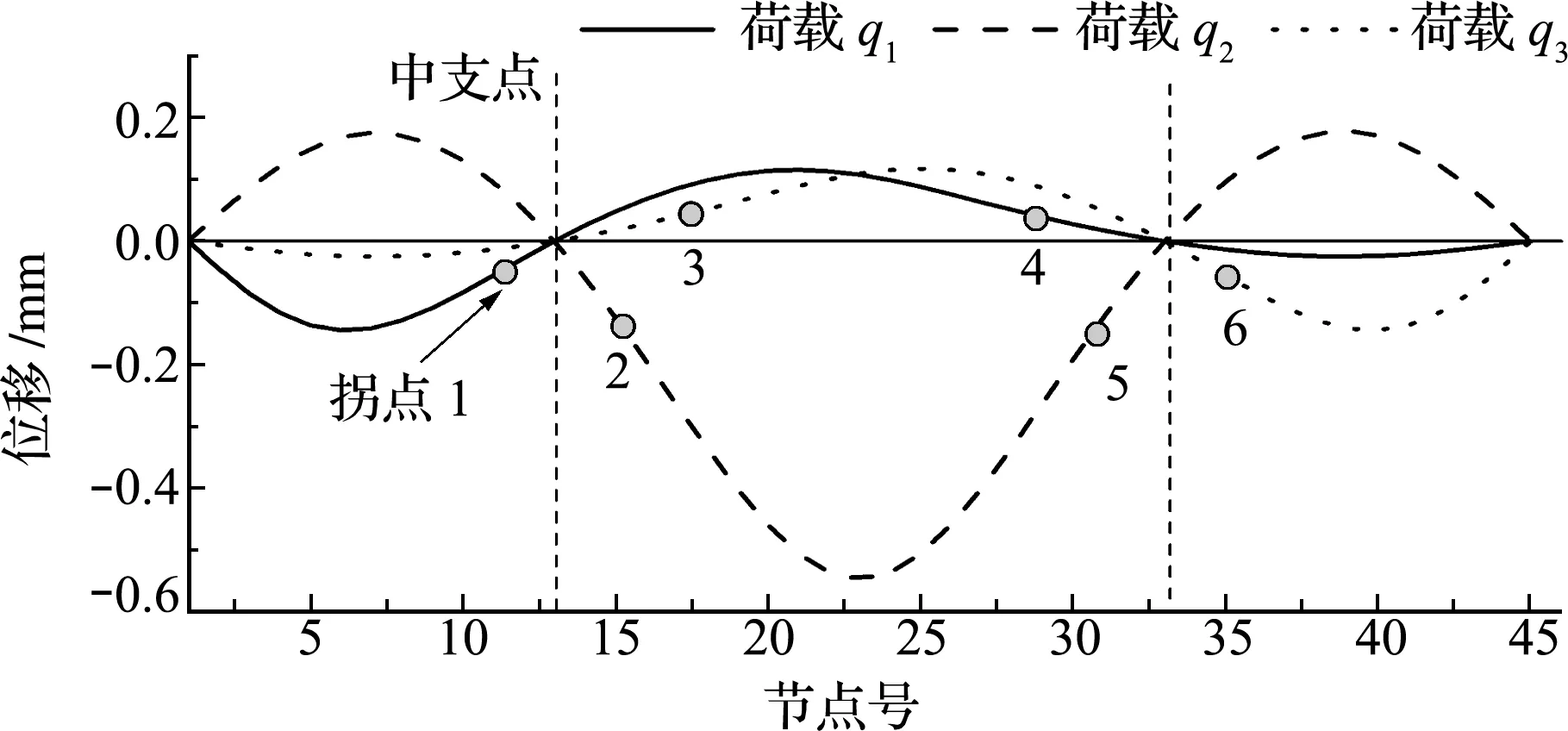
图7 均布荷载qi结构位移

Fig.7 Structural displacement diagram under uniform distributed loadqi

式中dFP=Fd-Fu为范数归一化振型损伤前后的柔度矩阵差；dF0=F0 d-F0 u为质量矩阵归一化振型损伤前后的柔度矩阵差，‖X‖f r o表示方阵X的Frobenius矩阵范数。

定义柔度差相对变化指标rdF如式(45)，用来反应不同振型归一化方法对柔度差的影响。

rdF=‖ζdFP-dF0‖f r o/‖F0 u‖f r o

(45)

为了比较所取模态阶数与柔度矩阵精度的关系，在Frobenius矩阵范数意义下定义误差指标为

δ=‖F-Ft‖f r o/‖Ft‖f ro

(46)

式中Ft为柔度矩阵理论值，通过计算结构上各点影响线构造得到。

显然，该误差指标为模态阶数的函数，绘制三跨连续梁柔度矩阵误差指标δ与所取模态阶数的关系曲线，如图8所示，1阶柔度矩阵误差为27.22%，2阶误差为15.35%，3阶误差为6.64%，5阶误差为 1.92%，之后很快收敛。因此，三跨连续梁选取误差最大的1阶和误差较小的5阶模态分析。

分析不同方法振型归一化下，三跨连续梁各损伤工况rdF与P范数的关系，如图9所示，1范数与3范数rdF的误差较为接近；2范数rdF误差最小；当P≥ 2时，rdF增速由大变小，最终趋于平缓；不同模态阶数的rdF有较小偏差。说明2-范数归一化振型计算的柔度矩阵与质量矩阵归一化振型的柔度矩阵最接近。

图8 柔度矩阵误差与模态阶数关系

Fig.8 Relationship between modal flexibility error and modal order

图9rdF与范数P关系

Fig.9 Relationship betweenrdFand normP

4.3 系数差xα和损伤程度De的关系

损伤识别方法采用逐跨均匀荷载面曲率差SULSC(the span-by-span uniform load surface curvature difference)指标，取P=0,1,2,3,5,10,30,80,150,300和∞。1阶和5阶模态分析结果如图10所示，其中损伤程度De取损伤单元左右节点的平均值，可见，系数差xα与De均近似呈线性关系，设拟合函数为De=kxα+b，De是关于xα的增函数，损伤程度10%的斜率基本在1.6～1.9，损伤程度20%的斜率基本在1.3～1.6，损伤程度30%的斜率基本在1.3及以下；不同工况比较发现，De越大，斜率k越小；各工况斜率k均小于2，故可根据xα和最大斜率2估算损伤程度的偏差。

连续梁在相同损伤程度下，不同位置单元损伤时，系数差xα与损伤程度De的关系均较为相似；不同损伤程度时，随着损伤程度的增加，系数差xα与损伤程度De的斜率减小，说明振型归一化方法对损伤程度的影响减小。

图10 系数差xα与损伤程度De的关系

Fig.10 Relationship betweenxαandDe

4.4 损伤识别

各损伤工况以5阶模态计算，得到不同P范数振型归一化损伤识别结果，取P=0，10和∞(对应rdF分别为最小、居中和最大)的结果如图11所示。工况1的rdFmax=0.006，P取任何值rdF都较小，定位精确且接近质量归一化，如图11(a)所示(图中定位指标DI最大值化为1)；工况2和工况3的rdFmax分别为0.017和0.022，相比质量矩阵振型归一化，10和∞-范数振型归一化在未损伤处有多个连续变化峰值，随着rdF增大，其干扰峰值越大，如图11(c，e)所示。三工况的损伤程度定量在不同振型归一化下有明显偏差，虽然单元30附近有较小峰值干扰，结合损伤定位指标可排除。

考虑柔度曲率指标的差异性，采用模态柔度曲率差MFC(the modal flexibility curvature difference)指标[10]对三跨连续梁进行对比分析，该指标先计算损伤前后柔度矩阵的曲率矩阵，

(47)

(48)

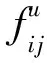
然后计算损伤前后柔度曲率矩阵的差值，并取各列的绝对最大值作为损伤识别指标MFC，即

MFC=max.|CFu-CFd|

(49)

以工况3为例，结果如图12所示。相比质量矩阵振型归一化，∞-范数振型归一化在单元38处无法识别损伤位置，在未损伤处有多个连续变化峰值易造成干扰，随着rdF增大，其干扰峰值越大，故不同振型归一化方法对MFC指标有较大影响。相比SULSC指标(图11(e))，在不同振型归一化方法下，MFC指标的损伤定位在损伤位置单元12和38的峰值较小，干扰峰值更容易影响损伤定位。

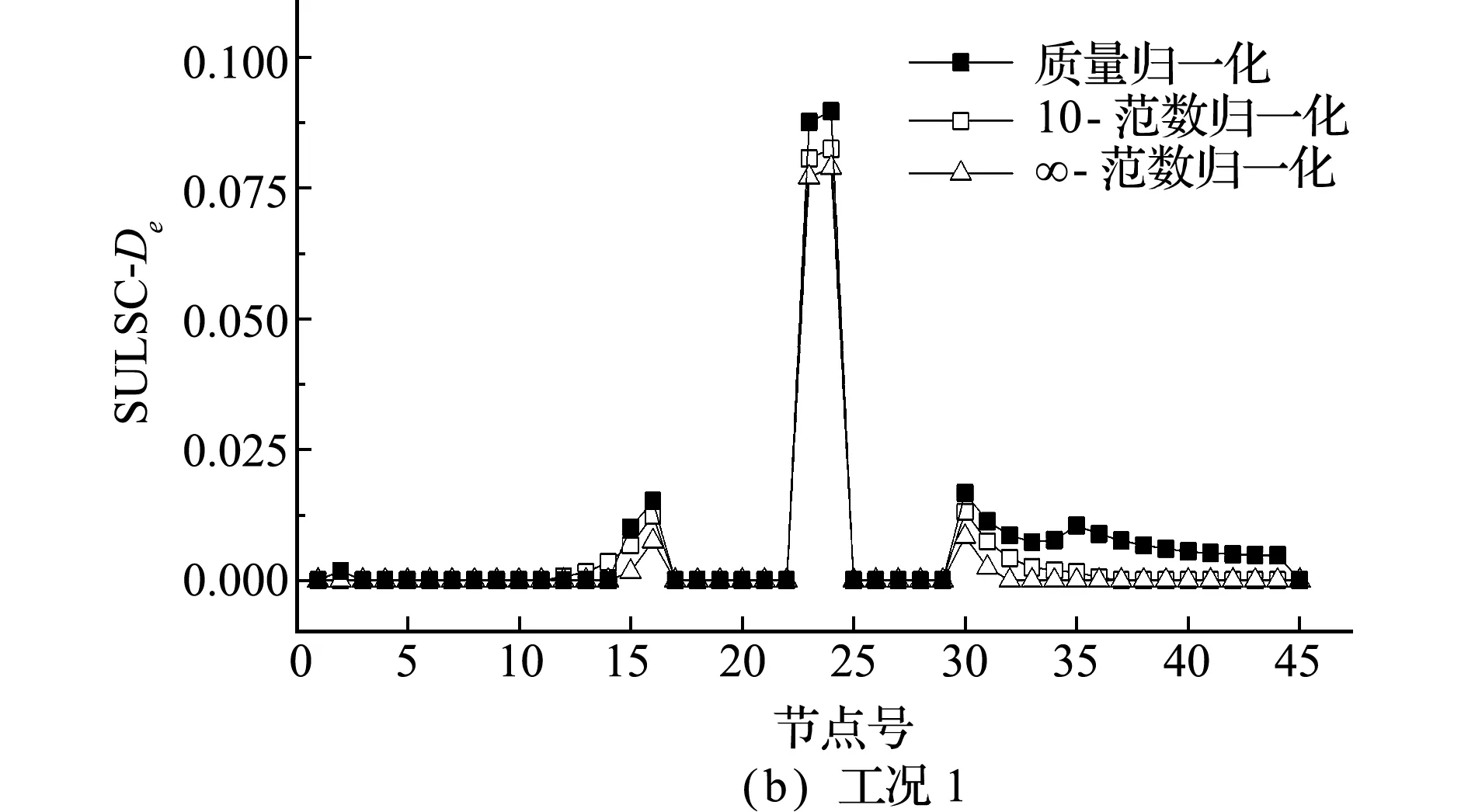
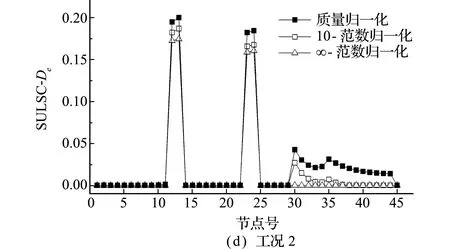
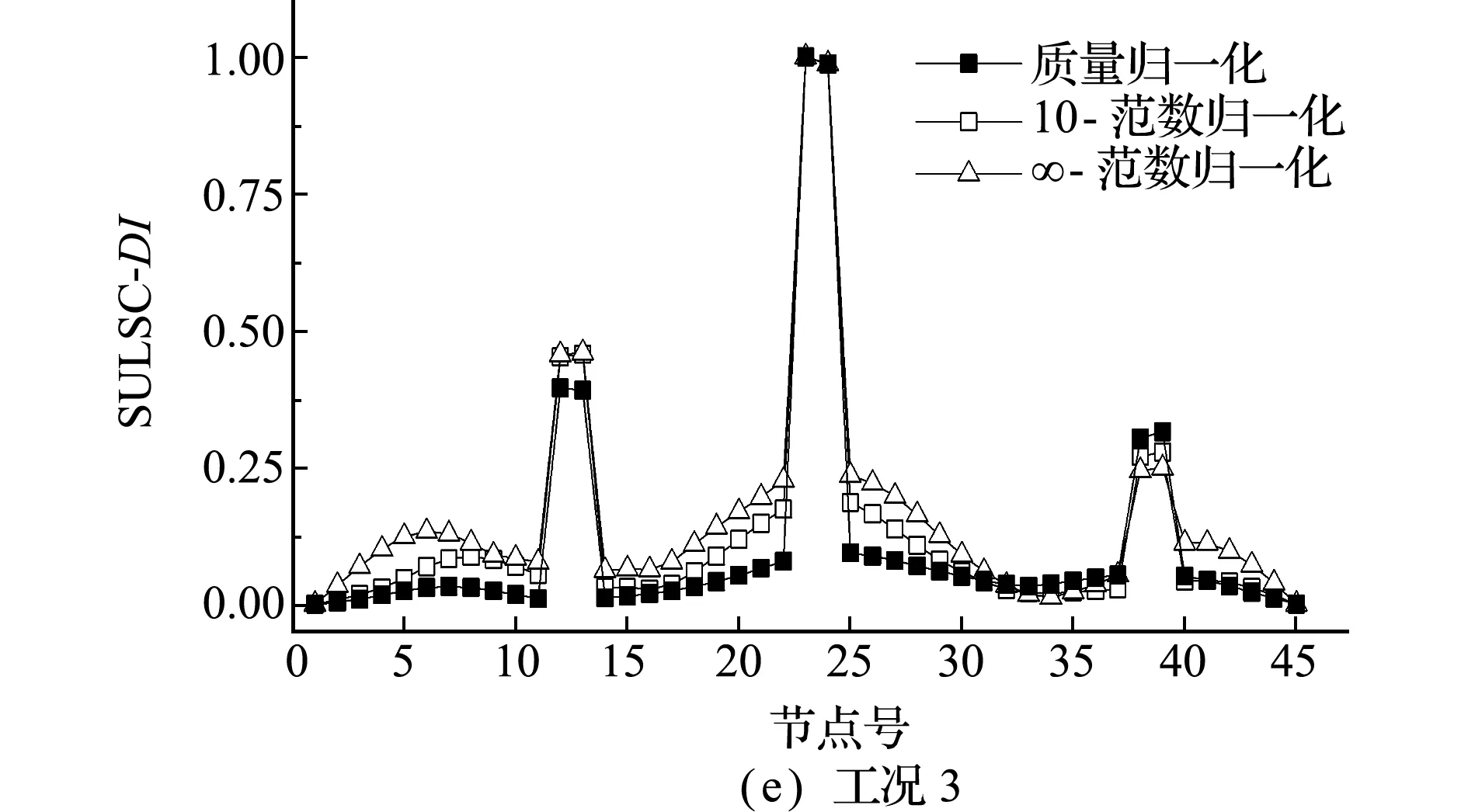
图11 指标损伤识别结果

Fig.11 Damage index identification results

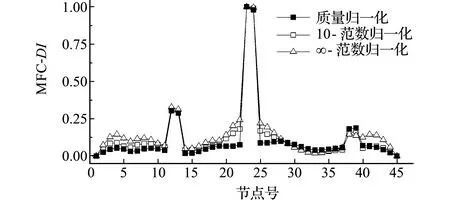
图12 工况3指标损伤识别结果

Fig.12 Damage index identification results under condition 3

5 结 语

(1)通过梁结构损伤前后均布荷载作用下的位移曲线，证明了位移曲率差指标可用于结构损伤定位；根据结构刚度、弯矩和位移曲率的关系，建立了由损伤前后位移曲率计算结构损伤程度的理论公式。由于ULS近似等于均布荷载作用的位移曲线，因此，采用模态类参数ULS代替静力位移曲线进行损伤识别，得到ULSC损伤定位和定量指标。对连续梁，由于位移曲线存在拐点，提出逐跨ULS曲率差损伤指标SULSC避免拐点影响。

(2)针对土木工程结构环境激励模态测试难以获得质量矩阵归一化振型，提出范数振型归一化方法。建立了ULSC指标在不同振型归一化方法下系数差xα与结构损伤程度De的关系，定量分析振型归一化方法对损伤程度识别的影响。

(3)对三跨连续梁，不同振型归一化下，系数差xα与SULSC指标损伤程度De呈线性关系，xα变化范围较小；当P取值较大时，柔度差相对变化rdF较大，结构损伤定位干扰变大；损伤程度定量偏差可由2xα估算。相比SULSC指标，不同振型归一化方法对MFC指标影响更大。

(4)梁式结构损伤识别使用柔度矩阵曲率类损伤指标时，若无法获得质量矩阵归一化振型，可采用2-范数归一化振型代替，其损伤识别结果与质量矩阵归一化振型结果最接近，这将有利于柔度曲率类损伤指标的实际应用。