网纹红土分数阶应力松弛模型
汪明武,徐新宇,周天龙,董景铨
(合肥工业大学 土木与水利工程学院,合肥 230009)
1 引 言
土体应力松弛特性与岩土工程的长期稳定性问题紧密相关,是岩土材料的重要流变特性之一,但基于已有文献报导[1],关于土体的松弛试验和模型的研究较蠕变本构关系研究要少的多。已有的土体松弛模型主要有经验模型[2]和元件模型,如西原模型[3,4]、Burgers模型[5,6]和广义Maxwell模型[7]等,但这些模型为整数阶模型,仅能描述线性粘弹性能,描述土体非线性流变行为存在局限性[8,9],且适用性较差[10],故为更真实准确反映土体的松弛时效特性,有必要进一步深入开展土体应力松弛模型的研究。而近期发展起来的分数阶微积分理论是整数阶微积分向任意阶的推广[11,12],并具有全局相关性好,物理意义明确,能更好描述岩土非线性力学行为的优点[13],为网纹红土松弛本构研究提供了新思路。学者将分数阶微积分理论应用于岩土体流变非线性的描述[14-20],取得了有效成果,如于怀昌等[10]建立了岩石分数阶Poynting-Thomson松弛模型;张春晓等[21]构建了膨胀土的三元件分数阶松弛模型;Liu等[22]推导了高阶分数导数本构模型,但至今罕有应用分数阶微积分理论针对网纹红土非线性松弛模型的研究。
本文基于分数阶微积分理论,推导了网纹红土的分数阶FVMS(Fractional Voigt and Maxwell model in series)松弛模型和分数阶FVMP(Fractional Voigt and Maxwell model in parallel)松弛模型,进而结合网纹红土的三轴松弛试验数据验证模型的适用性,为网纹红土的非线性松弛特性分析和长期稳定性评价提供依据。
2 分数阶应力松弛模型
2.1 分数阶微积分理论简介
分数阶微积分是指微分的阶数或积分的阶数不是整数,而是任意的实数或者复数,相对于整数阶微积分,可描述复杂的时效力学过程,刻画时间上的记忆性和空间上的路径依赖性。分数阶微积分的定义有多种形式[11],本文采用Riemann-Liouville 型分数阶微积分算子理论定义函数f(t)的分数,
(1)

(Re(β)>0)
(2)
分数阶的微积分Laplace公式为
(3)
式中s是变换参量,F(s)是f(t)的拉普拉斯变化。
基于Riemann-Liouville型分数阶微积分理论的软体元件本构模型方程为
σ(t)=ξdβε(t)/dtβ
(4)
式中σ(t)为应力,ε(t)为应变,t为时间,ξ为类粘滞系数。显然,当β=0,1时,软体元件退化成理想的弹塑性体和理想的流体。当ε(t)为常数,分数阶元件所描述的是松弛现象。
2.2 基于分数阶微积分的应力松弛模型
以往的非线性粘弹性本构关系大多是由弹性元件和粘性元件串联或并联来描述,基于分数阶的简单流变模型常用Maxwell模型和Kelvin模型,是时间的一个指数函数,而网纹红土成分复杂,且运动单元具有多重性,仅用一个松弛时间关系描述已不能满足实际要求,需发展拟合精度更高的多元件广义分数阶模型来描述[22]。为此,本文探讨了黏弹性四元件的FVMS模型和FVMP模型,如 图1 所示。


图1 四元件分数阶松弛模型
Fig.1 Fractional relaxation model of four elements
从图1(a)可以看出,根据元件的串并联法则可得
σ=σ1=σ2=σ3,ε=ε1+ε2+ε3
(5)
σ1=(E1+ξ1D1)ε1,σ2=ξ2D2ε2,σ3=E2ε3
(6)
式中σ为总应力;ε为总应变;σ1和ε1分别是分数阶Kelvin-Voigt模型中总应力和应变;σ2和σ3与ε2和ε3分别是分数阶Maxwell模型中分数阶元件和弹簧元件的应力和应变;E1和E2分别是两个弹簧的弹性模量;ξ1和ξ2为类粘滞系数;D1和D2是分数阶算子,D1=dβ1/dtβ1,D2=dβ2/dtβ2;β1和β2为分数阶阶数。联立式(5,6),可得
σ=G(t)ε
(7)
(8)
式中G(t)为松弛模量。令
(9)
(10)
对式(10)第一项进行级数变换,可得
(11)
对式(10)中各项进行拉普拉斯逆变化可得
(12)
(13,14)
将式(12~14)代入式(10),并结合式(9)可得FVMS模型的松弛模量为
(15)
从图1(b)可以看出,根据元件的串并联法则可得
σ=σ1=σ2+σ3,ε=ε1=ε2+ε3
(16)
σ1=(E1+ξ1D1)ε1,σ2=ξ2D2ε2,σ3=E2ε3
(17)
联立式(16,17),可得
(18)
对式(18)进行拉普拉斯变换,并令ε0(t)=ε0H(t), 则式(18)可变形为
(19)
式中ε0为初始应变,在应力松弛过程中为一恒定值。根据式(19)可得松弛模量的拉普拉斯逆变换式为
(20)
为得到式(20)的拉普拉斯逆变换,引入Mittag-Leffler(简称M-L)函数来完成。广义M-L函数的定义如下[11]。
M-L函数的拉普拉斯变换为

(22)
将式(20)与式(22)的第三部分进行对比,将式(20)第三部分中各参数取为k=0,v=1,u=β2,n=E2/ξ2,可得FVMP模型的松弛模量为
(23)
3 模型验证及参数识别
为验证本文提出的松弛模型的适用性和正确性。首先,采用基于GDS非饱和土三轴仪对网纹红土进行了不同应变条件下的应力松弛试验,并用上述的应力松弛模型对试验结果进行反演,确定了相关的模型参数。
3.1 三轴应力松弛试验
松弛试验用土取自安徽宣城地区,土体呈淡红色,物理性质指标列入表1。在围压σ3=300 kPa和吸力ua-uw=100 kPa的条件下,开展了应变水平分别为0.5%,0.75%,1.0%,1.45%,2.0%和4.0%的应力松弛试验。应力松弛试验主要由吸力平衡、等吸力固结、剪切及松弛阶段构成,不同应变水平下,网纹红土应力松弛试验的实测曲线如图2所示。
3.2 模型验证
本文选取L-M(Levenberg-Marquardt)算法确定模型的参数取值,可避免最小二乘法通常存在初始值选取不当的问题,根据式(15,23),采用L-M算法对图2的实验数据结果进行非线性拟合,模型参数结果列入表2和表3,拟合曲线如图3所示。
4 讨 论
由表2和表3可知,在不同加载条件下的应力松弛试验中,尽管分数阶FVMS模型和分数阶FVMP模型中的弹性模量E1和E2以及类粘滞系数ξ1和ξ2有一定的差异,但总体变化不大,而且拟合系数R2在0.989以上,最高达到 0.998,说明与实测数据误差较小。从图3可以看出,用FVMS松弛模型和FVMP松弛模型拟合试验数据可以得到较好的效果,且两者的分数阶模型都能很好地反映网纹红土松弛的应力快速下降和应力缓速下降两个阶段。同时可以看到,两个分数阶模型中的分数阶阶数β基本保持不变,限于篇幅,这里仅考虑分数阶阶数β的敏感性分析。在保持其他参数不变的条件下,如E1=3 kPa,E2=4 kPa,ξ1=5 kPa·d,ξ2=6 kPa·d,改变分数阶阶数β的数值,可以得到分数阶阶数β对本文提出模型在描述应力松弛行为时的影响,如图4所示。可以看出,分数阶数β的不同值主要影响FVMP模型松弛量的大小,对松弛速率影响较小;对FVMS模型松弛速率和松弛大小都影响较大。
表1 网纹红土的物理性质指标
Tab.1 Physical properties of net-like red soil

最大干密度/g·cm-3含水率/%液限/%塑限/%塑性指数最优含水率/%1.8123.648.528.220.017.9
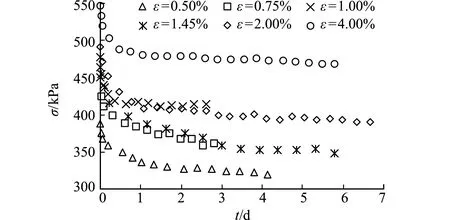
图2 网纹红土应力松弛实测曲线
Fig.2 Stress relaxation measured curve of net-like red soil
表2 FVMS模型参数拟合值
Tab.2 Fitted values of FVMS model parameters

ε/%E1/kPaE2/kPaξ1/kPa·dξ2/kPa·dβ1β2R20.50908.45306.202437.9855309.440.8510.580.9900.75563.26350.122648.2426957.480.8020.600.9971.00261.15398.034861.8236802.250.740.600.9911.45519.83346.681609.3221302.660.8330.610.9952.001374.07395.292335.4827596.270.8290.590.9974.00169.54453.303777.7823768.210.7500.620.996
表3 FVMP模型参数拟合值
Tab.3 Fitted values of FVMP model parameters

ε/%E1/kPaE2/kPaξ1/kPa·dξ2/kPa·dβ1β2R20.50311.5858.913.3662.090.7500.210.9890.75304.2581.5812.40328.230.7450.200.9941.00404.6035.335.9914.640.7420.200.9981.45336.46108.297.01119.670.7510.220.9952.00385.1983.496.4364.840.7670.240.9904.00462.5744.989.3135.160.7610.210.994
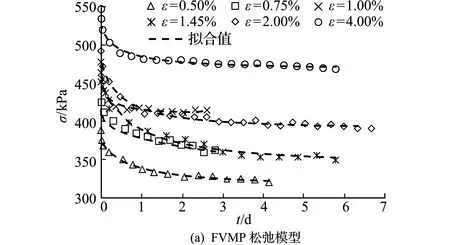

图3 FVMP松弛模型和FVMS松弛模型计算值和试验曲线实际值对比
Fig.3 Comparison of the calculated datas of FVMP model and FVMS model with the measured datas
为了定量描述本文提出的分数阶松弛模型反映网纹红土松弛时效特性的优越性,用应变为4%条件下的网纹红土应力松弛数据,分别对西原模型、Burgers模型以及本文提出的FVMS模型和FVMP模型进行拟合,并选取均方差(RMSE)、残差平方和(SSE)、相关系数(R2)、卡方系数以及F统计值作为定量的指标,结果列入表4。由表4可知,由于RMSE,SSE和卡方系数在描述拟合效果时,数值越小表示拟合精度越高,而R2和F统计值则是越大表示拟合效果更好,故综合五个指标值,本文提出的FVMS松弛模型和FVMP松弛模型拟合效果均优于西原模型及Burgers模型,也表明本文模型能较好地反映网纹红土应力松弛的全过程,拟合精度较高。
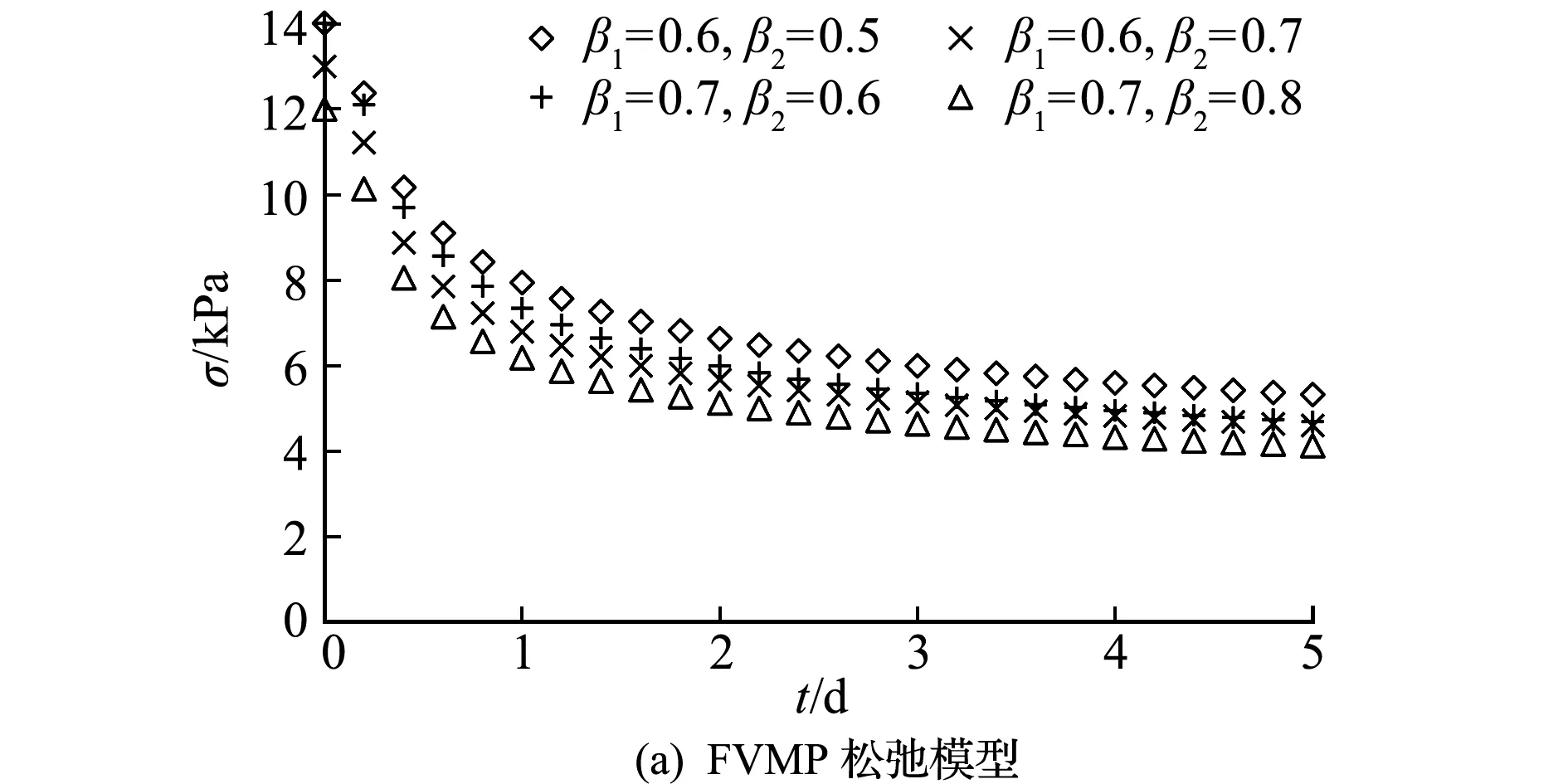

图4 不同分数阶阶数β下的FVMP模型和FVMS模型松弛曲线
Fig.4 Stress relaxation curve of various fractional orders of FVMP model and FVMS model
表4 模型拟合评价
Tab.4 Evaluation of fitting effects of various models

松弛模型RMSESSER2卡方系数F统计值西原模型2.32237.230.9860.233006.84Burgers模型2.43260.120.9900.252735.03FVMS模型1.65121.010.9960.125924.21FVMP模型2.05185.030.9940.183861.52
5 结 论
网纹红土是一种黏性土,应用整数阶模型很难刻画其松弛非线性特性和松弛全过程。本文基于分数阶微积分理论,探讨了网纹红土分数阶应力松弛模型,进而应用模型反演了实测三轴松弛数据,并与其他模型进行对比分析,得到如下结论。
(1)利用分数阶微积分理论,推导了网纹红土的FVMS松弛模型和FVMP松弛模型。构建模型公式推导严格,且具有明确物理意义,可实现网纹红土非线性松弛时效特性的准确描述。
(2)实测数据的模拟结果表明,本文的分数阶应力松弛模型模拟结果与试验实测结果吻合,并能有效模拟网纹红土的松弛全过程。
(3)对比西原模型和Burgers模型与FVMS松弛模型和FVMP松弛模型的拟合结果表明,本文推导的四元件分数阶应力松弛模型具有更高的可靠性和拟合精度,且参数较少,便于实际应用。同时,在讨论分数阶阶数敏感性时发现,分数阶阶数对两个分数阶模型的应力松弛量影响大,但对FVMS模型的松弛速率影响较小,而对FVMP模型的松弛速率影响则较大。

