高中数学分层教学研究——以试题分层解答为例

洪晓敏

(浙江省台州市天台平桥二中 317203)

新课程更加注重学生的差异性，提倡教师因材施教，以学生为本，遵循最近发展区理论，让学生都能够在自己能力的范围内进行学习和探究，从而提高学生的数学知识学习热情，不断提升学生的数学综合水平.教师可以根据班级学生的实际情况，采取分层练习、分层合作学习等策略，为不同层次的学生进行学习、提问、练习提供适合的习题，从而满足各个层次学生的需求.

一、类比变式，满足不同学生的思维

针对不同层次的学生，教师可以设置不同层次的问题，以便学生更好地探究.

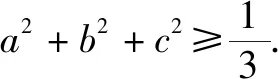
证明由已知得(a+b+c)2=1，

则a2+b2+c2+2ab+2ac+2bc=1.

由(a-b)2=a2-2ab+b2≥0得a2+b2≥2ab，同理得a2+c2≥2ac，c2+b2≥2bc.

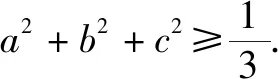
本题比较简单，适合数学基础能力弱的学生，可以帮助学生树立学习的信心，对于中等层次的学生，教师可以进行变式：

例题2 已知a+b+c=1(a,b,c∈R+)，那么a2+b2+c2是否有最小值?如果有，请求出其最值；没有请说明理由.

解题步骤和例题1比较类似，需要学生通过思考来得出答案，对于学生的能力进一步提升，适合中等层次的学生.对于思维能力强的学生，教师可以将试题的已知条件隐藏到题干中，以便学生进行探究.

本题对学生的能力要求较高，需要学生能够灵活运用换元思想，并能够发现题目中的隐含条件：logabca+logabcb+logabcc=logabcabc=1，这样，可以令logabca=m，logabcb=n，logabcc=k，这样试题又转化成例题1，从而有效地解决.

二、逐步递进，设计符合学生层次的问题

根据学生的实际水平，教师可以设计具有层次性的试题，以便所有学生都能够参与到实际的问题分析和解决中.

例题4 求等比数列2，4，8，16，…，2n的和Sn.

分析本题考查等比数列求和公式的运用，适合基础较差的学生，学生将数列中的数据代入即可.

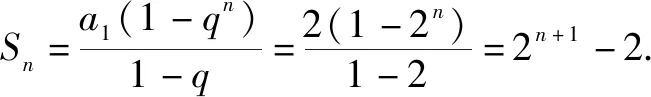
例题5 已知一个等比数列的前n项和Sn=48，前2n项和S2n=60，求此数列的前3n项和S3n.

分析看到试题，学生通常会进行联想，对比类似的问题，诸如等差数列{an}的前n项和Sn、n+1项至2n项之和Sn1，2n+1项至3n项之和Sn2，也成等差数列.然而，本题中的前2n项、前3n项与上述的问题还有区别，即问题中的S2n=Sn+Sn1，S3n=Sn+Sn1+Sn2.这样就需要学生进行具体分析，采用从一般到特殊的方法，有效地解决问题.

解得Sn2=3，S3n=S2n+Sn2=63.

分析本题的数列既不是等差数列，也不是等比数列，根据观察发现，数列的分子是首项为1，公差为2的等差数列，而分母则是首项为2，公比为2的等比数列，因此不能直接运用公式进行直接求解，需要学生将其进行转化，变为标准的数列，从而求解，对学生的思维能力和数学思想都有很高的要求，适合学生进行探究.

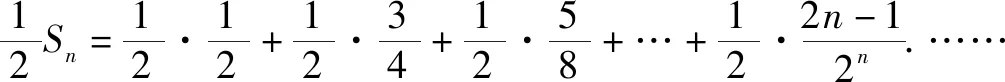
用①同分母减去②得：

三、因材施教，设计不同层次的习题

以往统一的习题模式，常常导致基础差的学生做不了，思维能力强的学生不够做.因此，高中数学要设计不同层次的习题，让所有学生都能够在课下进行探究，促进学生的发展.比如学习了古典概率以后，教师就可以设计以下三个层次的问题.

层次一，例题7 随机投一枚一元的硬币，能够出现“反面”的概率是多少？

例题8 随机将一枚骰子抛出，其出现“6”点的概率是多少？如果随机将2枚骰子抛出，出现点数和为奇数的概率是多少？

例题9 从1-5五个数字中随机取出两个数字，则所取出数字中含有“3”的概率是多少？

层次二，例题10 随机将2枚骰子抛出，则出现两个骰子点数相加大于7个概率是多少？

例题11 从1-5张扑克牌中依次取出2张，则第一张扑克的点数大于第二张点数的概率是多少？

层次三，例题12 我国古代典籍《周易》用“卦”描述万物的变化．每一“重卦”由从下到上排列的6个爻组成，爻分为阳爻“——”和阴爻“— —”，如图就是一重卦．在所有重卦中随机取一重卦，则该重卦恰有3个阳爻的概率是( ).

例题13 已知一只袋子中有黑色卡片a张，有白色卡片b张，卡片除了颜色不同外，其余没有差别，现在随机将卡片从袋子中一张一张地摸出来，求第n次摸出的卡片是白色卡片的概率(1≤n≤a+b).

总之，在高中数学分层教学中，教师要在课堂中和习题中进行分层，为学生布置适合学生层次的问题，这样才能让学生在已有的数学基础上进一步提升，提高学生的学习兴趣，满足学生的个性化、差异化学习需求，有效提高数学教学质量，落实核心素养的培养需求.