基于多目标优化算法的船舶微电网重构

苏丽，王锡淮，肖健梅

上海海事大学物流工程学院，上海201306

0 引 言

随着船舶大型化和自动化的发展趋势，其电力系统容量也在不断增加。一旦电力系统出现故障，一般可以采用粒子群［1-5］、遗传［6-9］、克隆［10］和差分［11-12］进化等算法对船舶微电网故障进行重构，从而迅速恢复重要负载的正常供电。然而，目前鲜有采用约束多目标优化算法进行船舶微电网重构方面的研究成果，这主要是因为多目标优化算法存在多个问题并行寻优、计算量大、操作困难等缺点。因此，寻求一种能够满足约束条件，同时令Pareto 解集收敛于最优非支配前沿且均匀分布的算法［13］是当前需要突破的难点之一。

近年来，已有学者开始尝试采用多目标优化算法来解决船舶微电网的重构问题。基于传统的非支配排序遗传算法（non-dominated sorting genetic algorithm，NSGA），张涛［9］提出了一种考虑精英选择策略和拥挤度的NSGA-II 算法，虽然其收敛性有所提高，收敛时间也大为缩短，但其没有充分地考虑约束条件。马理胜等［14］提出了一种基于混沌迁移及无参变异的差分进化算法，该算法结构简单，有效避免了早熟现象，但其淘汰了优秀不可行解，从而导致寻找最优非劣解的收敛性和分布性不佳。通过改进文献［14］的选择策略，马理胜等［15］将不可行解的优秀信息保存下来，从而提高了收敛性，但分布性差、收敛速度慢的问题尚待解决。

基于此，在重构微电网之前，本文将通过负载支路相关矩阵法［4］来确定部分负载的供电路径并计算支路负载的功率总和，这不仅可以减少数据分析量，还能为约束条件的建立奠定基础。约束多目标优化算法的优劣与约束条件的处理、进化算法的选取有很大关系［13］，所以本文拟提出一种两阶段差分进化（two-stage differential evolution，TSDE）算法：第1 阶段采用双种群混合法来处理约束优化问题，第2 阶段采用改进可行性法则来求解约束问题。同时，还将采用Tent映射混沌序列、改进的无参数变异算子和精英选择策略来进一步优化差分进化算法。最后，为了验证TSDE 算法的可行性及有效性，将与基于混沌迁移及无参数变异差分进化（chaotic migration and parameterless mutation differential evolution，CMPMDE）算法［14］、基于环境Pareto 支配选择差分进化（environment Pareto dominated selection differential evolution，EPDSDE）算法［15］的仿真结果进行对比，用以为船舶微电网故障重构设计提供参考。

1 船舶微电网重构的数学模型

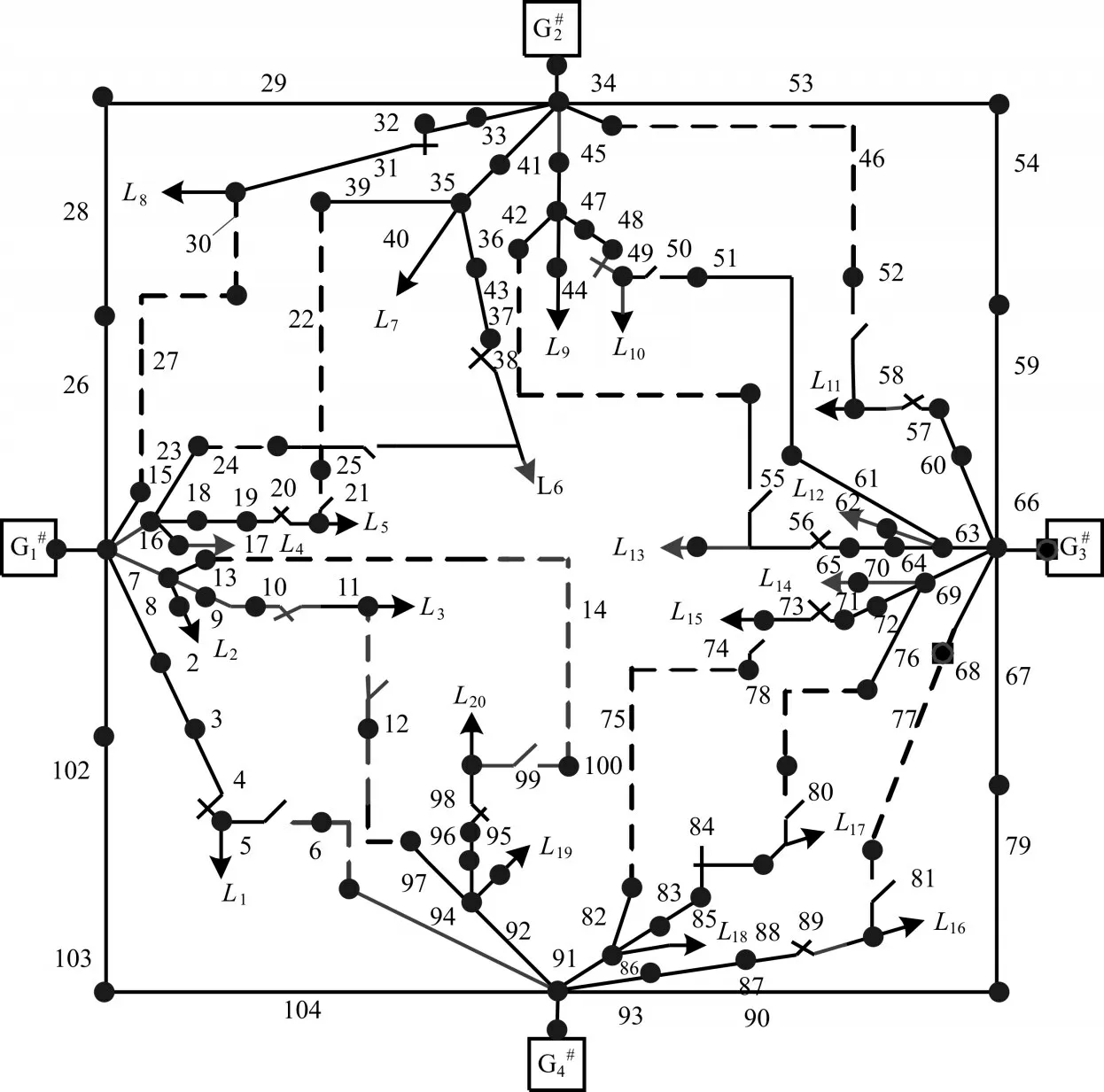
图1 供电系统结构示意图Fig.1 Schematic diagram of power supply system

3）若G≤S，进入第4）步；否则进入第5）步。

4）第1 阶段：首先，采用式（7）和式（8）分别产生初始化第1 种群P1和第2 种群P2，采用式（9）和式（10）分别对P1和P2的个体进行离散化操作，并采用式（1）、式（2）、式（4）、式（5）和式（6）分别计算第1 种群的目标函数值和第2 种群的目标函数值、约束程度；然后，对P1和P2中的父代个体分别进行变异和交叉操作，从而产生子代种群Q1和Q2；最后，根据2.4.1 节的选择策略，分别选出P1和P2的N*个优秀个体。

5）第2 阶段：首先，将第1 阶段进化之后的第1 种群和第2 种群合并为1 个种群，将其作为第2阶段的父代种群P，并根据式（1）、式（2）、式（4）和式（6）计算父代种群的目标函数值和约束程度；然后，对父代种群P 进行变异和交叉操作，从而产生子代种群Q；最后，根据2.4.2 节的选择策略，选出优秀的可行解集Z1和不可行解集Z2。

6）判断终止条件，如果G＜Gmax，即返回第3步；否则终止算法，输出可行解集。

4 实验仿真分析

本文将采用环型船舶电网拓扑结构作为仿真模型（图1），其负载属性如表1 所示。为了将本文提出的TSDE 算法与CMPMDE 算法［14］、EPDSDE 算法［15］进行对比，在仿真环节设置了相同的参数和故障，具体如下：

1）参数设置。将初始化开关状态设为负载编码值等于1，第1 种群和第2 种群的规模设为N=50，可行解集和不可行解集分别设为N1=50 和N2=25，平衡系数λ=0.2，交叉因子初始值CR0=0.85，最大迭代次数Gmax=50，而S 的取值则可以根据实际故障情况确定。

2）故障1。假设支路B10，B63遭到破坏，导致负载L12卸载，负载L3，L13的正常供电路径损坏，负载L10的备用供电路径损坏。

3）故障2。假设1 号发电机G1#因故障停止供电，导致负载L2，L4卸载，负载L1，L3，L5的正常供电路径损坏，负载L6，L8，L20的备用供电路径损坏。

将3 种算法独立运行50 次，并随机选择一次运行结果。为了减少人为选择时间，提高微电网重构效率，本文将TSDE 算法的多个解择优为一个最优非支配解，其中最少负荷失电量是主要的考量因素。3 种算法在故障1 和故障2 工况下的仿真对比结果分别如表2 和表3 所示。

由表2 和表3 可知：在故障1 工况下，TSDE 算法所得最优非劣解的最小负荷失电量比CMPMDE 算法和EPDSDE 算法小185 A，其最小开关操作数比CMPMDE 算法多1 次，与EPDSDE 算法相同；在故障2 工况下，TSDE 算法的最小负荷失电量比CMPMDE 算法和EPDSDE 算法小940 A，其最小开关操作数比CMPMDE 算法和EPDSDE 算法少1 次。根据Pareto 支配和Pareto 最优解的定义可知：在故障1 工况下，TSDE 算法与CMPMDE算法的最优非劣解互不支配，但TSDE 算法获得的最优非劣解支配EPDSDE 算法，即TSDE 算法的最优非劣解优于EPDSDE 算法；在故障2 工况下，TSDE 算法获得的最优非劣解均可支配CMPMDE算法和EPDSDE 算法，即TSDE 算法的最优非劣解优于CMPMDE 算法和EPDSDE 算法。综上所述，TSDE 算法的收敛性明显优于CMPMDE 算法和EPDSDE 算法。

表2 在故障1 工况下，不同算法的重构结果对比Table 2 Comparison of different methods for reconfiguration results under fault 1

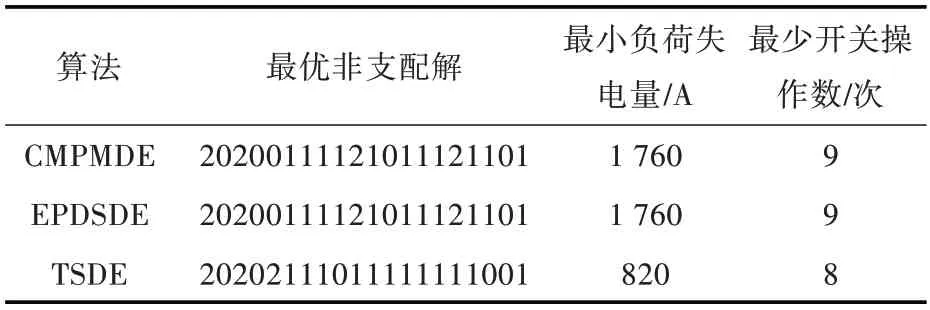
表3 在故障2 工况下，不同算法的重构结果对比Table 3 Comparison of different methods for reconfiguration results under fault 2

一旦船舶出现故障，应在满足约束条件的前提下立即恢复无故障负载，所以重构时间是一项非常重要的性能指标。将TSDE 算法独立运行50次之后，统计其最佳收敛代数GENbest、平均收敛代数GENavr、最佳收敛时间Tbest和平均收敛时间Tavr，并与文献［14］和文献［15］的记录数据进行对比，其结果如表4 和表5 所示。由于文献［14］和文献［15］中没有CMPMDE 算法和EPDSDE 算法的运行时间数据，故表4 和表5 对应位置为空白。

由表4 可知，在故障1 工况下，TSDE 算法收敛至最优非劣解集的最佳迭代次数比CMPMDE 算法和EPDSDE 算法大19 次，其平均迭代次数则大17.8 次。由表5 可知，在故障2 工况下，TSDE 算法收敛至最优非劣解集的最佳迭代次数比CMPMDE算法和EPDSDE 算法分别大25 次和24 次，其平均迭代次数则分别大25次和24.5次。由此可见，表4和表5 中的最佳迭代次数和平均迭代次数均大于CMPMDE 算法和EPDSDE 算法，这是因为在第一阶段采用了双种群混合法（即自适应罚函数法和可行性法则）来处理约束优化问题，并采用改进的选择策略同时对可行解和不可行解进行选择，所以增加了种群的多样性并扩大了种群规模，从而导致了收敛速度相对较慢。但根据表4 和表5 的仿真结果，TSDE 算法的最优收敛时间和平均收敛时间都控制在10 s 以内，可以满足船舶微电网的重构时间要求。

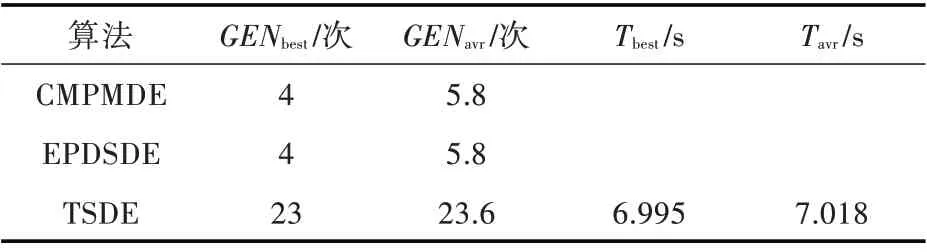
表4 在故障1 工况下，不同算法的重构时间对比Table 4 Comparison of different methods for reconfiguration time under fault 1

表5 在故障2 工况下，不同算法的重构时间对比Table 5 Comparison of different methods forreconfiguration times under fault 2

为了对比3 种算法Pareto 最优解集的均匀性与逼近性，将3 种算法独立运行50 次，并随机选择一次运行结果，如图2 和图3 所示。根据仿真结果，TSDE 算法的Pareto 前沿在均匀性和逼近性方面均优于CMPMDE 算法和EPDSDE 算法。

综上所述，虽然TSDE 算法的收敛速度略逊于其他2 种算法，但其可调参数更少、收敛性和分布性更优，更适用于实际工程需求，可以保证船舶电力系统的安全稳定运行。

图2 在故障1 工况下，不同算法的多目标函数值Fig.2 Multi-objective function values of different algorithms under fault 1

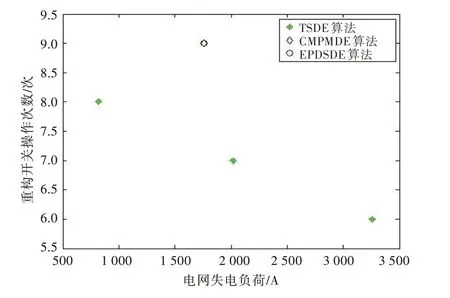
图3 在故障2 工况下，不同算法的多目标函数值Fig.3 Multi-objective function values of different algorithms under fault 2

5 结 语

为了求解船舶微电网的重构问题，本文提出了一种基于两阶段差分进化算法的约束多目标优化方法。在第1 阶段，利用双种群混合法求解约束优化问题，再将优化后的第1 种群和第2 种群合并为1 个种群。这不仅可以让自适应罚函数法和可行性法则进行优劣互补，还增加了种群多样性，从而提高了寻找最优非劣解的收敛性和分布性。在第2 阶段，采用改进的可行性法则处理约束优化问题，并采用一种基于环境Pareto 支配选择策略来保留可行解和不可行解的优秀信息。经过第2 阶段的优化处理，进一步改善了TSDE 算法的收敛性和分布性。除此之外，本文还引入了Tent映射混沌序列、改进无参数变异算子、自适应交叉因子和改进的精英选择策略，从而进一步改善了差分进化算法的重构性能。

根据2 种故障工况下的仿真对比结果，TSDE算法的非支配解分布更为均匀，同时更接近真实的Pareto 前沿，故其更适用于处理船舶微电网故障重构方面的问题。