三体船屈服强度的可靠性研究

周渝航，冯国庆，张旭辉

哈尔滨工程大学船舶工程学院，黑龙江哈尔滨150001

0 引 言

屈服破坏是船体结构多种失效模式中最主要的失效模式之一，而对新型船舶进行屈服强度评估尤为必要。高速三体船作为近年来的新型高技术船舶，以甲板空间大、平稳性能好、航行阻力小、耐波性良好等特点被广泛使用。三体船具有独特的连接桥结构，两侧片体和船中主体共享一个主甲板，因此上层建筑面积大。在三体船的结构强度评估中，上述结构部位都需要被重点关注。目前，船体结构屈服强度直接计算主要采用基于等效设计波法的确定性方法，其中许用应力标准主要采用第四强度理论von Mises 应力标准。但因作用在船体上的载荷、结构形式和材料性能等这些随机变量具有不确定性，所以采用可靠性方法进行强度评估更为科学。

结构可靠性分析方法在船舶与海洋工程领域中的应用起步于20 世纪70 年代。 Nordenstram［1］认为波浪弯矩服从Weibull 分布，利用全概率法分析了船体失效概率。Faulkner 等［2］论述了结构可靠性分析中局部安全因子法和安全指数法的基本原理，并应用到了船体甲板屈曲失效模式的总纵强度分析设计中。冯国庆等［3］通过建立船体结构屈服强度衡准的极限状态方程，对一艘散货船屈服强度的可靠性进行了分析。Paik［4］分别采用船体梁的中心安全因子法和一次二阶矩法对双层底油船进行了可靠性评估。目前，对于三体船这类新型高技术船舶，还没有充分的强度可靠性研究。

本文将基于第四强度理论［5］的von Mises 应力，采用直接计算方法，建立屈服强度衡准的极限状态方程，对某三体船船体结构的屈服强度进行评估。通过模拟真实海况，得到作用于船体上的波浪载荷，进而得到船体结构的von Mises 应力，通过组合各短期海况的单元应力分布，得到应力长期分布和极值分布，并由极限状态方程和均值一次二阶矩法得到失效概率、可靠性指标和安全系数。同时，分析随机因素对可靠性分析的影响。

1 屈服强度可靠性分析基本原理

短期海况不规则波作用下的船体结构单元应力是通过线性叠加多个规则波得到的。通过对时域分析得到各短期海况下应力分布的概率密度函数进行加权组合，得到船体结构单元应力的长期分布，再结合序列统计学原理，得到应力的极值分布函数；然后根据第四强度理论和均值一次二阶矩法得到失效概率与安全系数，对船体屈服强度可靠性进行分析。

屈服强度可靠性分析的流程如图1 所示。

图1 屈服强度可靠性分析流程图Fig.1 Flow chart of yield strength reliability analysis

1.1 船体结构单元短期应力分布

为了获得结构单元的von Mises 应力短期分布，根据海浪谱（采用皮尔逊-莫斯科维奇谱）对短期海况下的不规则波进行模拟。本文将短期海况对应的有效频段分成若干份（29 个频率数），不规则波是由其叠加而来。

依据能量关系，各规则波波幅ai为［6］

式中：Δωi为各规则波的频率间距，rad/s；S(ωi)为相对应的海浪谱密度。

船体结构应力响应幅值的正应力σmn和剪应力τmn（m，n 分别代表x或y方向）可通过将单位波幅规则波的波浪载荷分解为实部及虚部，分别进行加载，求解得到应力响应的实部σR和虚部σI，从而获得的应力响应幅值σ和相位ξ为［7］：

由规则波中的应力响应可知：对于波幅为ai，频率为ωi，初相位为εi的余弦规则波，其应力各分量也为余弦波形，则可采用式（4）进行线性叠加，得到不规则波下应力的时间历程σn(t)。

式中：σn(t)为所选取计算单元中心点中面的正应力及梁单元的轴向应力，MPa；σn0为各个方向静水载荷下的正应力及梁单元轴向应力，MPa。

根据式（1）～式（4），得到各短期海况下结构单元的合成von Mises 应力时间历程：

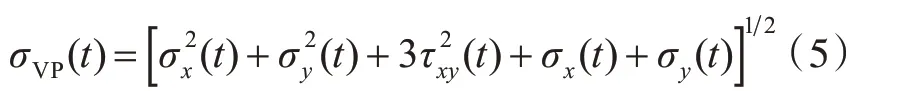
依据所得的短期海况下板单元和梁单元的von Mises 应力时间历程，可得到应力峰值的短期分布概率密度函数f0(x)。

1.2 船体结构单元应力长期分布与极值分布

由时域分析得到的各短期概率密度函数f0(x)，加权组合得到von Mises 应力峰值的长期概率密度函数f(x)［8］，即

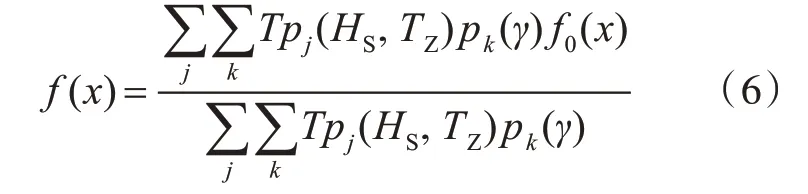
式中：pj(HS，TZ)为某一种海况出现的概率，其中HS，TZ分别为某一种海浪谱表达式中对应的有义波高和波浪跨0 周期；pk(γ)为航向角k出现的概率；j代表海况；T为单位时间内的载荷循环次数。

根据概率密度函数f(x)及其分布函数F(x)，并以yN为单元von Mises 应力峰值在波浪中遭遇的最大值，则根据序列统计学原理［9］，极值分布函数G(yN)为

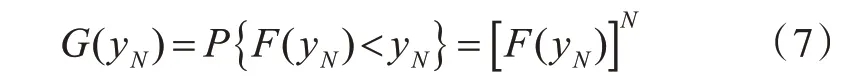
则极值分布概率密度函数g(yN)为

根据第四强度理论，单元屈服失效概率［10］

式中：C 为结构极限强度；D 为载荷；σs为屈服强度；φ为计算结构形式的变异系数。

按照可靠性指标β的定义，可得

式中，Φ为一种分布函数。

本文采用安全系数法对结构进行评估，根据均值一次二阶矩法，得到安全系数K0如下［11］：

式中：μf，μC，μD分别为极限状态方程f=C-D，C和D 的均值；σf，σC，σD分别为f，C 和D 的标准差；δC，δD分别为C 和D 的变异系数。

2 实船计算参数

2.1 实船主尺度及模型

本研究涉及的实船主尺度参数及有限元模型分别如表1 和图2 所示。

2.2 波浪载荷参数

作用在船体上的波浪载荷参数如表2 所示。

表1 三体船主尺度参数Table 1 Principle dimensions of trimaran

图2 三体船有限元模型Fig.2 Finite element model of trimaran

表2 波浪载荷参数Table 2 Wave load parameters

2.3 有限元计算单元及编号

选取三体船特有结构的4 个板单元和3 个梁单元为研究对象，单元位置及编号如图3 所示。

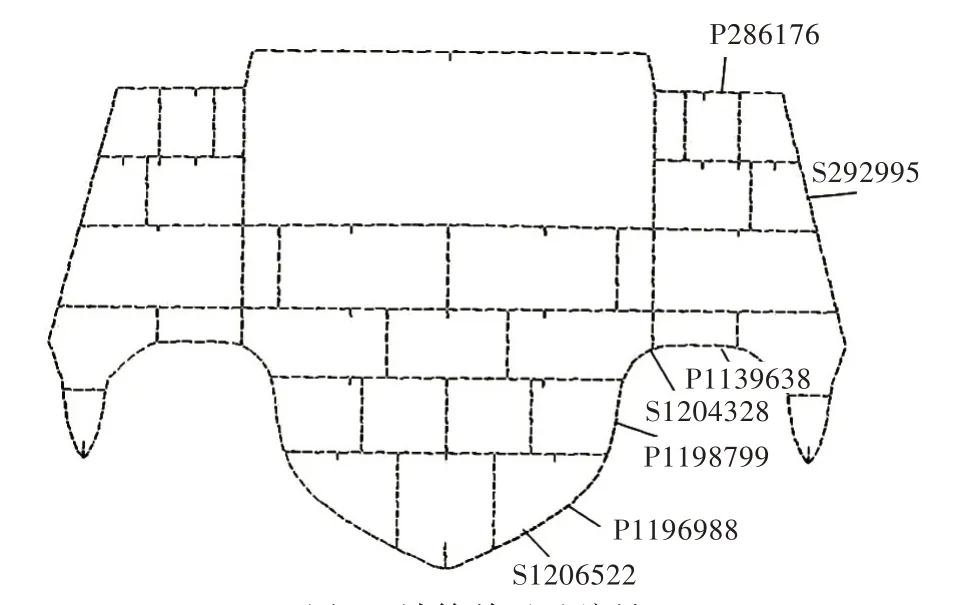
图3 计算单元及编号Fig.3 Calculation unit and numbers

3 屈服强度可靠性分析

3.1 单元应力短期分布

根据本研究所选取的浪向和频率，通过波浪载荷计算软件得到每个单位波幅规则子波作用下船体所受载荷的实部和虚部，将实部和虚部分别加载到有限元模型上，再由式（2）和式（3）得到各浪向角、各频率的单位波幅规则波下板单元中面中心点x，y方向的正应力及剪应力，进而根据式（4）和式（5）得到短期应力时历曲线。

在短期海况HS=12.5 m，TZ=8.5 s，浪向角为150°时，板单元P1139638 的von Mises 应力时历曲线如图4 所示，梁单元S1204328 的von Mises 应力时历曲线如图5 所示。

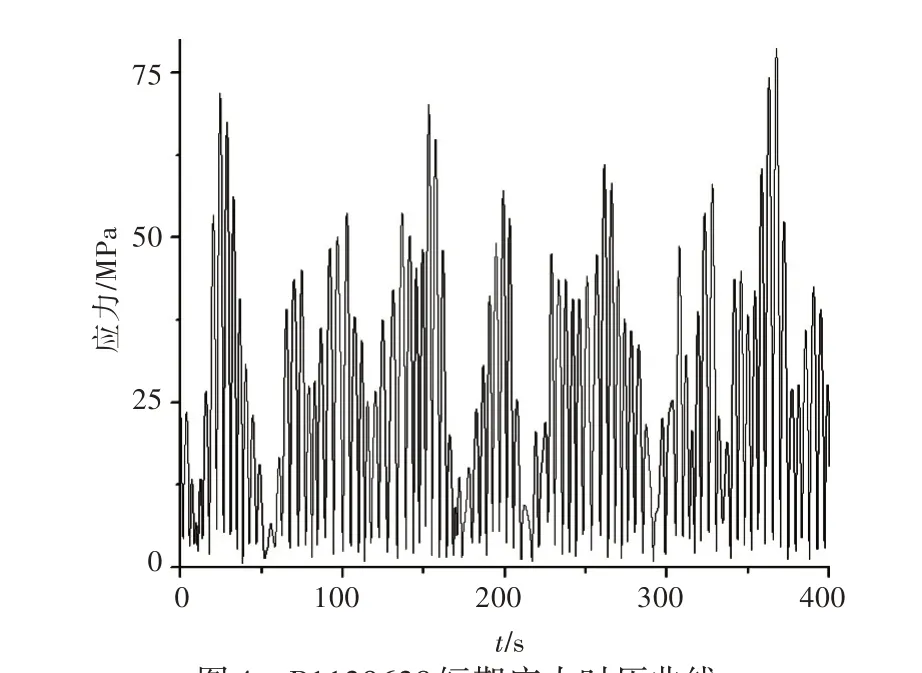
图4 P1139638 短期应力时历曲线Fig.4 Short-term stress time history curve for P1139638

图5 S1204328 短期应力时历曲线Fig.5 Short-term stress time history curve for S1204328

经研究发现，该三体船短期应力分布的概率密度拟合曲线与双参数的Weibull 分布曲线吻合度较高，因此推断该三体船的短期应力分布概率密度函数为

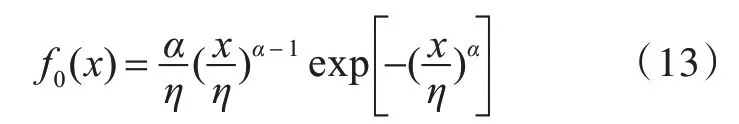
式中：α为Weibull 分布的形状参数；η为威布尔分布的尺度参数，MPa；x为x轴的坐标值。

通过拟合曲线，得出选取的7 个单元的双参数如表3 所示。

由表3 可以看出：板单元P286176 的尺度参数较小，即应力概率分布函数离散度较小，经分析，这与三体船中和轴较高、甲板部分承受总纵弯曲应力小有关。 板单元P1139638 及梁单元S1204328 的尺度参数要大于其他单元，即应力概率分布的离散度较大，经分析，这是由于这2 个单元位于三体船连接桥的结构部位。该处的应力分布符合三体船的结构特点。

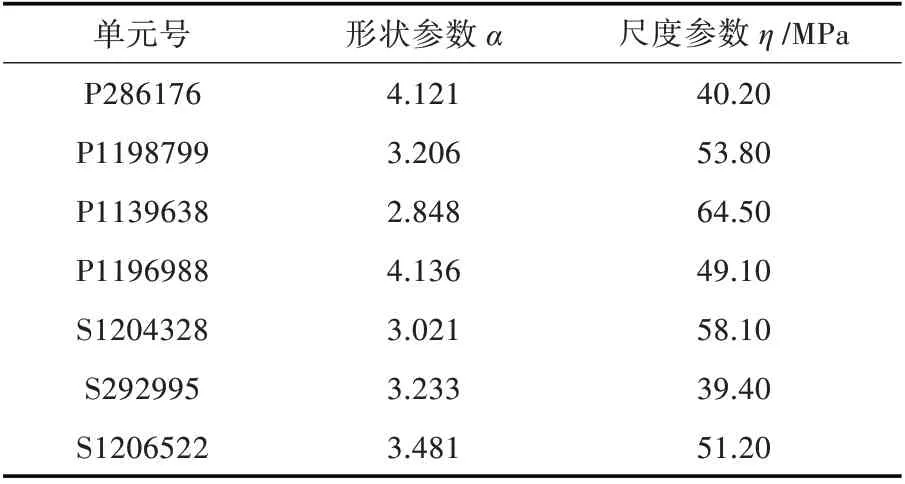
表3 短期应力概率密度函数双参数Table 3 Probability density function of double parameters for short-term stress

3.2 单元应力长期分布和极值分布

通过各短期概率密度函数f0(x)，根据式（6）得到单元von Mises 应力的长期分布，进而根据式（8）可算得基于序列统计学原理的极值分布概率密度函数。 板单元P1139638 及梁单元S1204328 的极值概率密度拟合曲线g0(x)分别如图6 及图7 所示。

图6 P1139638 极值概率密度拟合曲线Fig.6 Extreme probability density fitting curve of P1139638

图7 S1204328 极值概率密度拟合曲线Fig.7 Extreme probability density fitting curve of S1204328

经拟合发现，三体船单元应力极值分布同样符合对数正态分布，其概率密度函数可表示为

式中：λ为对数应力极值的标准差；h 为对数应力极值的平均值。通过计算分析，本文计算的船体单元的双参数值如表4 所示。

表4 极值分布双参数拟合值Table 4 Two-parameters fitted values of extreme value distribution

3.3 单元屈服可靠性分析

假设本文所考虑的结构形式不确定性的分布为正态分布［12］，其均值为1，变异系数φ=0.1，0.3，0.4；材料屈服极限服从对数正态分布，其均值为310 MPa，变异系数δC=0.06，0.07。由船体结构的von Mises应力的极值分布，根据式（9）～式（12），计算得到4 个板单元及3 个梁单元的β，Pf及K0。当φ=0.1，δC=0.07 时，结果如表5 所示。

表5 单元可靠性计算结果（φ=0.1，δC=0.07）Tab.5 Calculation results of elements reliability（φ=0.1，δC=0.07）

分析表5 可知：

1）对于屈服应力与屈服极限比值较大的结构，可靠性指标β较小，失效概率Pf较大，安全因子K0较小。通过对表5 中板单元P1198799 和P1139638 与其他板单元进行比较，可以看出这一趋势。另由图2 可以看出，上述2 个板单元位于三体船连接桥部位，且此处为整船较危险的部位。

2）对比文献［3］可知，本文所选取的三体船与常规油船、散货船等船型相比，失效概率较大，可靠性指标较低。

3）由表中数据与文献［3］中有限元屈服衡准对比，本文所得结果符合船体强度的分布规律，故可以认为从概率角度研究船体屈服失效同样适用于三体船，且所述三体船的特殊部位结构的失效概率较大。

3.4 屈服可靠性影响因素分析

为了分析船体可靠性的影响因素，根据本研究中所涉及到的可能因素，分别针对φ及δc做了进一步分析，以连接桥部位的板单元P1139638 为例，分析结果如表6 所示。

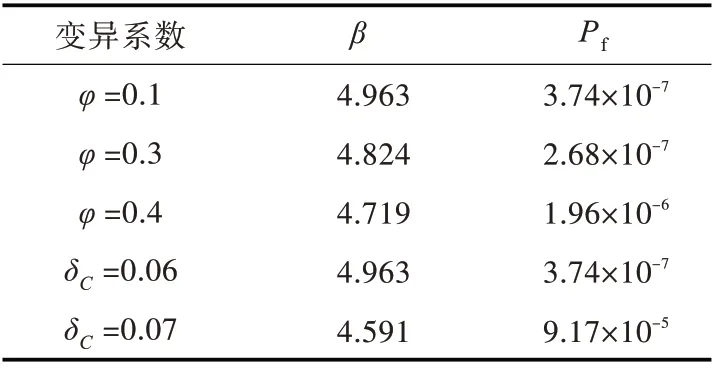
表6 对比分析计算结果Table 6 Calculation results of comparing analysis

由表6 可知：

1）对于结构形式的不确定性，变异系数φ越小，校核单元的可靠性指标越好，失效概率越低。

2）对于材料不确定性，变异系数δC越小，校核单元的可靠性指标越好，失效概率越低，并且从表中数据可知，材料不确定性对可靠性指标的影响比模型不确定性大。

4 结 论

本研究充分考虑了船体上变量和作用载荷的随机性，运用概率的思想对一艘三体船的屈服强度进行了可靠性分析，得到的结论如下：

1）三体船短期von Mises 应力时历分布可以拟合为双参数的威布尔分布，应力长期分布可拟合为对数正态分布。通过拟合曲线可知，三体船连接桥处及附近位置应力较大，因三体船上层建筑大，导致中和轴较高，故甲板处应力较低。

2）在三体船连接桥的位置，可靠性指标较低，失效概率较高。通过可靠性分析的方法得到的结论与传统确定性方法大体一致，即屈服因子较大处失效概率较大，安全因子较低。

3）模型不确定性和材料不确定性对可靠性指标有影响，变异系数越低，可靠性指标越高。材料的不确定性是较大的影响因素。