带保护区和比率依赖响应函数的Lesile模型的正解的局部分支分析
2020-06-28 07:46施越曾宪忠
河西学院学报 2020年2期
施 越 曾 宪 忠
(湖南科技大学数学与计算科学学院,湖南 湘潭 411201)
1 引言
生物数学模型的研究最早可以追溯到20 世纪20 年代由Lotka 和Volterra 建立的经典的捕食模型.Lotka和Volterra建立的模型只考虑物种数量(或密度)随时间的变化,没有考虑捕食者和食饵对空间变量的依赖,因而,建立的模型是常微分方程组动力系统.实际情况下物种的分布是依赖于空间的,它们有一种自扩散运动,即物种由种群密度高的地方向种群密度低的运动.此外该模型也没有考虑捕食者消化食饵的时间,食饵和捕食者相互制约的问题.如考虑上述问题,则可以建立比率依赖的食饵捕食者模型.对于濒危物种而言,由于其自然增长率较低,如果捕食者对它的捕食量较大,那将会造成濒危物种灭绝,因此,有必要建立一个保护区来保护濒危物种.
本文研究下列捕食模型[1-3]相应的稳态问题的正稳解的局部存在性
对于生物保护区,尽管已有部分研究,但是由于各类问题的复杂性和对象的多样性,因而仍有许多问题需要解决,例如有些物种的增长不是Logistic型[2],捕食者容量与食饵密切相关的.上述问题不仅有明确的实际意义和广阔的应用前景,而且具有一定的研究难度,因此对这类问题研究是非常有必要的.
显然,(1.1)有一个奇异的平凡解(0,0)和一个半平凡解(λ,0).本文使用比较原理和极值原理得到解的基本估计,再利用局部分支定理得到(1.1)解的局部存在性.
2 预备知识
由文献[2-6]可知有引理

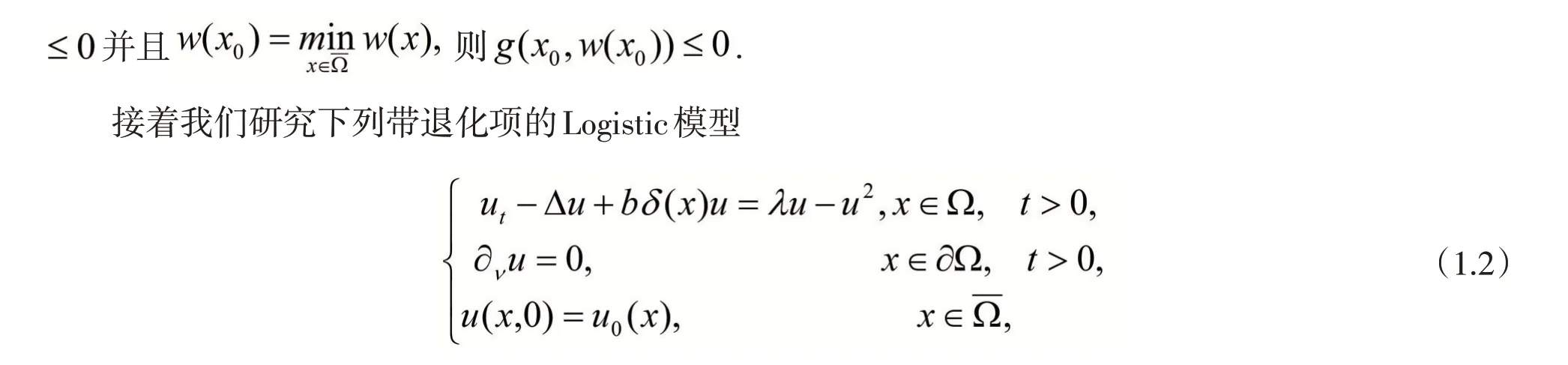
相应的稳态问题为

3 (1.1)解的估计
该部分首先利用极值原理[6]对(1.1)正解及参数进行估计,然后利用Crandall-Rabinowitz局部分支定理[7-9]对问题(1.1)的局部正解进行讨论.


4 (1.1)解的局部存在性


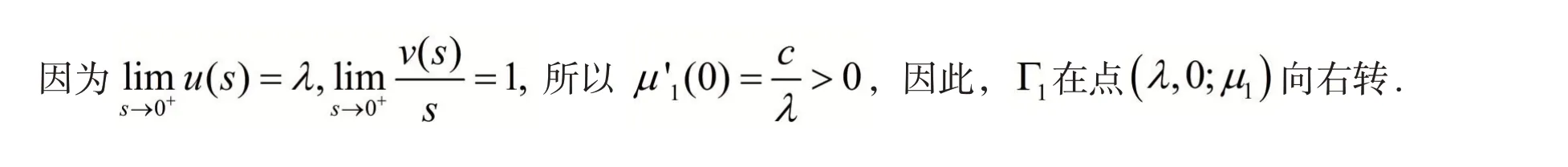
猜你喜欢
数学物理学报(2022年5期)2022-10-09
延边大学学报(自然科学版)(2022年2期)2022-09-13
黑龙江大学自然科学学报(2022年1期)2022-03-29
六盘水师范学院学报(2021年6期)2022-01-09
计算机系统应用(2021年10期)2022-01-06
百科探秘·海底世界(2020年11期)2020-12-31
数学大世界(2020年23期)2020-09-14
学生天地(2019年28期)2019-08-25
动漫星空(兴趣英语)(2018年4期)2018-10-30
上海师范大学学报·自然科学版(2018年3期)2018-05-14

