基于模糊控制技术的磨机控制系统设计应用研究

樊 毅 冯兴隆 管孝强 王 剑 王 平 石 峰

(1.云南迪庆有色金属有限责任公司，云南 香格里拉 674400；2.北京矿冶科技集团有限公司，北京 100160；3.金属矿山智能开采技术北京市重点实验室，北京 102628)

目前，国内日处理万吨级以上的铜矿山磨机润滑控制系统设计理念比较陈旧和传统，它绝大部分是应用理想环境状态下的信号检测与控制进行设计[1-3]。未能解决电磁干扰、粉尘、油污、振动等恶劣环境影响故障停车频发问题。不能进行磨机机械病态预测，一旦发生故障，机械损伤将扩大。而且不可以通过在线运行故障处理的办法，减少磨机非计划停车频次。同时，磨机停车后，会发生再启动开车困难的问题。

究其根源，此类超大型重点设备控制系统存在如下缺陷：1)无外围传感器信号失真与否的甄别判断和分类推送控制功能；2)无对机械性能的预测性控制功能；3)无在线运行故障处理功能。据不完全统计，磨机故障停车将造成重大的经济损失。此外，大量的停车善后处理，额外增加员工的高强度体力劳动，增加安全风险。运用模糊控制技术，探寻一种最佳的适用值，通过外围传感器失真与否甄别有效信号，通过处理有效信号，避免假性报警造成的频繁停车。基于模糊控制技术的磨机控制系统设计成功运用于普朗铜矿中，并产生了极大的经济效益，对其他矿山建设及未来智能化矿山自动化技术应用具有一定的借鉴意义。

1 优化控制策略

甄别控制处理单元获取小齿轮红外温差、小齿轮红外温度、油流、油压、轴承温度以及振动范围，通过模糊控制[3-4]判断失真情况。判断为失真信号，则不参与逻辑连锁控制，进入历史数据记录单元储存，仅供查询使用。判断为真实信号，则将数据传送给逻辑连锁控制单元，参与运行连锁控制[1-2]。

逻辑连锁控制单元接收到甄别控制处理单元的数据信号后，对信号进行分析，判断故障问题，利用模糊控制[3-4]寻找最佳使用值得设定值：根据矿山实际情况，每个温度传感器设定-200 ℃的断线温度，检测到该温度时，直接将信息传输至在线故障处理单元，并发出报警信号；设定正常使用温度值为60 ℃，超高温度90 ℃，超出超高温度值时，发出该检测点的故障停机指令，并发出报警信息；对小齿轮小端的温差范围，根据红外温度传感器的信息，设定两端温差值正常范围为15 ℃，超大温差值为30 ℃，温差值超过15 ℃时，发出报警信号，超过30 ℃时，则发出故障停机指令。对供油管道的油压，设定正常使用范围的低压为40 kg/cm3、超低压为15 kg/cm3的预设值，当信号达到该值时输出相应检测点的报警信息或故障停机指令。

在线故障处理单元主要针对两类故障处理，分别是润滑油故障处理和温度检测故障处理，具体处理方式为：润滑油故障进行不停机在线处理，包括润滑油故障处理等待间歇和计时置零两个功能，润滑油喷射周期结束后预设等待间歇时间，等待间歇时间功能中加入计时置零功能，在等待间歇时间内进行润滑油系统的故障处理，等待间歇时间中启动计时置零功能，令等待间歇时间重新开始计时，保证故障处理具有充分时间，在机械润滑允许的情况下，可以无限次使用，直到问题解决完成，之后再进行大小齿轮的甘油喷射润滑。温度检测故障处理，对每个温度传感器的线路和探头进行监测，任意一个温度传感器发出断线故障时，显示断线信息，提示维护人员针对性检查和处理，避免因高温产生故障，导致停车。

预测控制处理单元，根据实时检测数据和历史数据在线趋势记录，结合设备性能的正常使用范围指标值域，设定正常运行的超出区域界限值，检测数据超出区域界限值时，提前预警，通知维护人员提前对设备的轴承、轴瓦、齿轮等机械结构进行性能分析和保养维护。

2 模糊控制策略、规则

2.1 模糊控制判断失真情况步骤

1)确定模糊控制器模型及输入语言(误差、误差变化率)、输出语言的变量，本模糊控制模型采用双输入单输出(单输入单输出寻找结果过于理想化、简单化，不适用)的二维模糊控制器[4-5]：

输入变量：偏差变量为e，偏差变化率ec；

偏差e=r-y，r为失真度设定值，y为失真度测试值；

偏差变化率ec(k)=e(k)-e(k-1)，(k=0，1，2，……)；

2)输入语言变量偏差e、偏差变化ec和输出语言变量控制量变化U的语言值的确定：

偏差e的基本论域：[-20次，+20次]；

输出语言变量：失真度测试过程中控制滤波时间长度的变化量U；

偏差语言值e的离散论域：

X={-6，…，0，…，+6}；

则偏差e的量化因子为：

Ke=2×6/[20-(-20)]=0.3；

偏差E的语言值选为：PB，PM，PS，PO，NO，NS，NM，NB共8个值；

确定在X论域上模糊子集PB，PM，PS，PO，NO，NS，NM，NB的隶属度函数μ(x)，并建立语言变量E的赋值表；

偏差变化率ec的基本论域：[-15，+15]；

偏差变化率语言值ec的离散论域：

Y={-6，-5，…，0 …，+5，+6}；

则偏差变化率ec的量化因子为：

Kec=2×6/[15-(-15)]=0.4；

语言变量偏差ec的语言值选为：PB，PM，PS，ZO，NS，NM，NB共7个值；

确定在论域X上用以描述模糊子集PB，…，NB的隶属度函数u(y)，并建立语言变量ec的赋值表，参考表1的e建立ec赋值表。

控制量变化u的基本论域：[-10 s，+10 s]；

控制量变化语言值U的离散论域：

Z={-7，-6，…，0，…，+6，+7}；

则控制量变化u的比例因子为：

Ku=[10-(-10)]/2×7=10/7；

语言变量控制量变化U的语言值选为：PB，PM，PS，ZO，NS，NM，NB7个语言值；

通过长期应用总结，确定在论域Z上用以描述模糊子集PB，…，NB的隶属函数μ(z)，并据此建立语言变量U的赋值表，参考表1的e建立U赋值表。

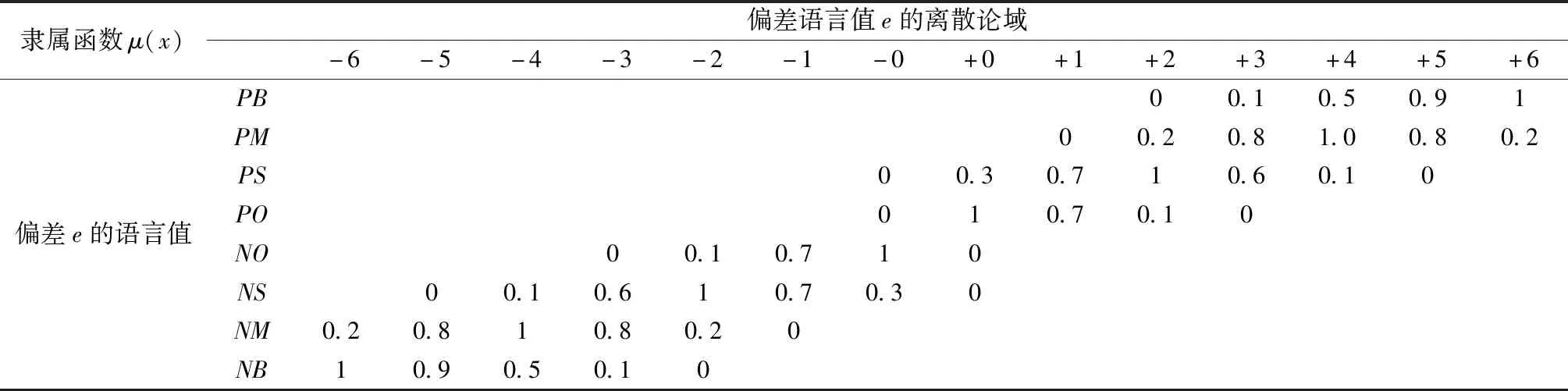
表1 语言变量e的赋值表(省略值为0)Table 1 Assignment table of language variable e

3)模糊控制规则的确定：

当误差e较大时，选择控制量u以尽快消除误差为主；当误差e较小时，选择控制量u要注意防止超调，根据上述规则，得到以下模糊控制表：

表2 模糊控制规则表Table 2 Fuzzy control rules

得到该失真度偏差、偏差变化率与滤波时间长度之间的模糊关系R：

R=(E×U)(EC×U)=E×EC×U

=(NBE×NBEC×PBU)∪(NME×NBEC×PBU)∪(NSE×NBEC×PMU)∪……

其中规则内的模糊集取交集运算，规则间的模糊集取并集运算；

4)模糊化与模糊推理：

设实测偏差为e(k)，ec(k)=e(k)-e(k-1)，(k=0，1，2，……)

量化后得e*，ec*

且e*∈X={-6，-5，…，-0，+0，…，+5，+6}，ec*∈Y={-6，-5，…，0，…，+5，+6}

将e*、ec*模糊化得模糊子集E*、EC*

则U*=(E*×EC*)R，即模糊控制器的输出为误差向量、误差变化率向量与模糊关系的合成；

5)控制量的反模糊化：

解模糊与模糊控制表的生成，采用最大隶属度法对模糊控制增量进行解模糊，得到在论域Z={-7，…，0，…，+7}上取值的控制增量u*，对论域X(X={-6，…，-0，+0，…，+6})和论域Y(Y={-6，…，0，…，+6})的全部元素所有组合进行上述模糊化、模糊推理及模糊判决运算，均能得到论域Z(Z={-7，…，0，…，+7})上的元素与之一一对应，将这些对应关系制成表格，即得模糊控制表。

表3 模糊控制查询表Table 3 Fuzzy control query table

模糊控制表离线计算得到：根据U*=(E*×EC*)R，在E*=(PB，PM，PS，PO，NO，NS，NM，NB)，EC*=(PB，PM，PS，ZO，NS，NM，NB)时，计算控制器的输出模糊向量U*，再按照“最大隶属度法”进行反模糊化，则选择控制量为U*在(PB，PM，PS，ZO，NS，NM，NB)上计算的最大值，即为U*max值填入以上模糊控制查询表。

在线控制时，在每一控制周期将实测偏差e(k)、ec(k)，(k=0，1，2，……)分别进行量化，取得查找模糊控制表所需的e*、ec*，再从表中查出对应的控制量变化u*，与比例因子ku相乘，便得到用于被控对象的实际控制量的变化值u，即u=u*×ku。

本模糊控制的目的去掉失真度，则包含了e≤0的所有u*，另外ku=10/7；结合实际运行历史数据趋势波形图来看滤波时间的设置应不小于5 s，通过u=u*×ku≥5 s计算，得出u*≥3.5，所以，在该模糊控制器下，所有u*>3的控制量均可以达到去掉失真度的要求；但是u*选择过大，实际控制量的变化值u也会过大，即滤波时间增大，导致控制系统出现进入逻辑控制等单元的正常信号严重滞后，系统对外部正常信号处理不及时，严重超调，失去系统的优越性，所以最佳失真度的控制量u*应该满足：3

2.2 利用模糊控制寻找最佳使用值的设定值

参考失真度模糊控制设计过程对磨机控制系统最佳设定值的寻找。

1)确定模糊控制器模型及输入语言、输出语言变量，采用双输入单输出的二维模糊控制器模型：

输入语言变量：偏差语言变量为e，偏差变化率ec；

偏差e=r-y，r为各设定值的目标值，y为多次的测试值；

偏差变化率ec(k)=e(k)-e(k-1)，(k=0，1，2，……)；

输出语言变量：设定目标稳定运行过程中控制设定值长度的变化量U；

2)输入语言变量偏差e、偏差变化ec和输出语言变量控制量U变化语言值的确定；组成二维坐标系，采用三角形或半梯形的隶属度函数关系进行模糊计算；

3)确定模糊控制规则：

按上述控制规则，得到该失真度偏差、偏差变化率与滤波时间长度之间的模糊关系R：

R=(E×U)(EC×U)=E×EC×U=(NBE×NBEC×PBU)∪(NME×NBEC×PBU)∪(NSE×NBEC×PMU)∪……

4)模糊化与模糊推理：

设实测偏差为e(k)，ec(k)=e(k)-e(k-1)，(k=0，1，2，……)

量化后得e*、ec*

且e*∈X={-6，-5，…，-0，+0，…，+5，+6}

ec*∈Y={-6，-5，…，0，…，+5，+6}

将e*和ec*模糊化得模糊子集E*和EC*

则U*=(E*×EC*)R，即模糊控制器的输出为误差向量、误差变化率向量与模糊关系的合成；

5)控制量的反模糊化：

采用最大隶属度法对模糊控制增量进行解模糊，得到在论域Z={-7，…，0，…，+7}上取值的控制增量u*；对论域X(X={-6，…，-0，+0，…，+6})和论域Y(Y={-6，…，0，…，+6})的全部元素所有组合进行上述模糊化、模糊推理及模糊判决运算，得到论域Z(Z={-7，…，0，…，+7})上的元素与之一一对应，将这些对应关系制成模糊控制查询表。

模糊控制查询表离线计算得到：

根据U*=(E*×EC*)R，在E*=(PB，PM，PS，PO，NO，NS，NM，NB)，EC*=(PB，PM，PS，ZO，NS，NM，NB)时，计算控制器的输出模糊向量U*，再按照“最大隶属度法”进行反模糊化，则选择控制量为U*在(PB，PM，PS，ZO，NS，NM，NB)上计算的最大值，即为U*max值填入以上模糊控制查询表；

在线控制时，在每一控制周期将实测偏差e(k)、ec(k)，(k=0，1，2，……)分别进行量化，取得查找模糊控制表所需的e*、ec*，再从表中查出对应的控制量变化u*，与比例因子ku相乘，便得到用于被控对象的实际控制量的变化值u，即u=u*×ku；

根据上述模糊控制设计得出以下设定值控制设置结论：

(1)红外温差报警的最佳设定值寻找：

选择：报警值的控制量变化u的基本论域：[-15，+15]；

控制量变化u的比例因子为：Ku=[15-(-15)]/2×7=15/7；

由上述推导u=u*×ku计算得出，u*=7。满足最大隶属度取值原则，所以上述报警值的最佳设定为15 ℃；

(2)红外温差故障停机的最佳设定值寻找：

选择：报警值的控制量变化u的基本论域：[-30，+30]；

则控制量变化u的比例因子为：Ku=[30-(-30)]/2×7=30/7；

由上述推导u=u*×ku计算得出，u*=7，满足最大隶属度取值原则，所以上述故障停机值的最佳设定为30 ℃。

3 工业应用

该技术现已经成功运用在普朗铜矿，该设计结构简单，设计科学，使用方便，对所有外部传感器检测信号进行甄别处理，避免失真信号进入逻辑连锁控制单元，避免磨机因假性报警和故障的频繁停机；增加了机械性能预测性控制功能，有效控制轴承、轴瓦、齿轮等机械损伤程度；增加在线运行故障处理功能，实现了不需要停机就可以对齿轮润滑油润滑、温度检测等故障进行处理，减少磨机非必须停车频次。经过该项技术开发应用后，增加该矿山年度生产直接经济收益约6 000万元，提高单系列设备全年运转效率约为4.1%，在高原环境下，减少员工高强度额外体力劳动，提高员工身心健康指数，降低安全风险。

4 结论

基于模糊控制技术，通过对磨机控制系统进行优化研究并应用后，其设备的综合优越性能得以充分发挥出来，磨机运转效率全面提升、生产成本大幅度降低。该项优化控制策略对其他行业而言，仍然值得推崇，前景广阔。