1种通过声带空气动力学模型求解发声阈值压力的方法
张莉丽,王 琰,陈莉媛,肖仲喆,张晓俊,陶 智
(苏州大学 光电科学与工程学院,江苏 苏州 215000)
嗓音的产生来源于肺部气流引起的声带振动,其中发声阈值压力是嗓音功能的1个重要指标.当肺部气压达到阈值压力时,气流向声带传递足够的能量克服声带组织耗散所带来的损失,使声带产生大幅度振荡,再经过口腔辐射最终产生嗓音输出.从功能上讲,发声阈值压力是能够产生声带振动所需要的最低能量指数,在主观感受上表现为发声的力度和发声的容易程度.因此发声阈值压力的研究对于更好地理解嗓音产生机理具有重要意义.
发声阈值压力最早由Titze[1]于1988年提出.在临床上,其可作为声带功能健康的指标,也可作为量化嗓音情感和声带疲劳度的客观指标,反映了声带黏性程度的变化[2].研究人员利用物理模型[3-4]、离体喉[5]和真人测量[6]等方式来探究与发声阈值压力相关的理论和临床意义.Titze[1]根据二质量模型在发声时的声带表面压力分布推导出发声阈值压力与预发声声门直径、跨声门压系数成正比,与声带长度成反比.此外,为了测试阈值压力与声门半径的关系,Titze等[7]采用树脂玻璃搭建半喉模型,在这个模型中通过螺旋调节声门半径,并在声带表面覆盖1层薄硅胶膜,硅胶膜中可以循环不同粘度的液体来模拟声带的不同种情况,实验证实了阈值压力与预发声声门直径成正比,与声带长度成反比.但实验结果在声门直径等于零时,测得的阈值压力并不为零,与通过二质量模型得到的结果不相符.为了探究这一原因,Lucero[8]考虑在声门直径较小时增加黏性效应,对发声阈值压力表达式修正,通过泊肃叶效应求解声门直径较小时声带内的黏性效应,这种修正与Titze等[7]得到的实验结果基本吻合.后来,Chan等[9]考虑将粘膜波和声道的惯性阻抗作为自激振动的主要能量传递机制,实验得到的结果与阈值压力表达式和声门半径之间的关系在图像的上升和下降趋势上保持一致,但斜率上存在差异,推测可能是由于未考虑声门直径比较小时声带内的黏性效应所导致的,但与Lucero[8]获得的表达式在声门直径较小的情况仍然存在很大的差异.Fulcher等[10]根据入口损失系数和出口系数计算声带表面压力分布,并且将计算得到的值与实验结果进行对比,得出了这2种系数与声门直径和跨声门压之间的关系.近年来,随着数值方法的发展和计算能力的提高,数值计算模型被广泛地应用于发声过程中声门内流场变化和声带振动的分析[11-12].数值计算模型通过离散化求解流体力学中的Navier-Stokes控制方程,考虑肺部产生的动态激励源对发声的作用,将气流运动和声带振动相结合,更符合嗓音的实际产生过程[13].
现有的发声阈值压力推导出的结果并不能完全预测发声阈值压力的表达形式,与实验结果均有较大差异,因此有必要从发声原理角度研究阈值压力的具体表现形式.本文从声带振动特性的角度出发,建立声带的空气动力学模型对声门内流场进行数值求解,得出声带表面压力和声门内气流的体积流量,进而推导出声门直径与入口损失系数的关系,对发声阈值压力的表达式进行修正,并将求解出的发声阈值压力表达式与前人的实验结果拟合,验证修正后发声阈值压力表达式的准确性.
1 声带空气动力学建模的阈值压力修正
1.1 发声阈值压力表达式的求解缺陷
发声阈值压力即为能使声带产生振荡的最小肺部气压[1],根据二质量块运动的稳定性,求得发声阈值压力表达式为
(1)

Chan等[9]于2006年建立了1个半喉的硬塑模型,将阈值压力与声带振动部分的线性黏弹性剪切特性和上声道的惯性电抗联系起来,并在物理模型上进行了额外的实验,将粘弹性生物材料植入人工声道内,包括透明质酸(Hyaluronic Acid, HA)、纤维连接蛋白(Hyaluronic Acid with FibroNectin, HA with FN),对声带组织粘弹性在发声阈值压力上的效应进行评估.实验过程中,声门下压力从0开始逐渐增大,直至声带出现稳定的自激振荡.对比不同浓度的透明质酸和纤维连接蛋白添加至声带表皮得到的发声阈值压力结果,发现当预发声声门直径很小时,发声阈值压力并不为0,而式(1)的结果与实验得到的结果在预发声声门直径等于0时不一致.
上述实验结果说明仅从发声驱动力的角度并不能给发声阈值压力以很好的修正.而声带的空气动力学模型可以依据声带和声门的精确尺寸制成,并可以精确地控制声带的跨声门压和声带运动,通过声带气动仿真模型研究声带内的压力变化可以对发声阈值压力的表达式进行修正.
1.2 声带空气动力学模型和数值求解过程
根据声带的生理组织结构,以声门为基本气流通道建立声带的空气动力学模型,利用流体动力学计算软件Fluent对声门管内流场进行数值计算,得出声带表面受力和声门内气体的体积流量,以探究预发声声门直径的改变对声带受力和声门内气流分布的影响.
根据Scherer等[14]建立的M5声带模型,声门入口的形状采用以声门角度为变量的半径来定义,声门出入口曲线用直线连接起来构成声带表面.由于在刚性模型中压力剖面的经验性结果表明声门形状不会在前后逐渐变尖,相对较尖锐的声门入口与声带上皮的实际情况不太一致,因此将其改为圆形入口,以更符合声带的实际生理结构.

图1 声带的空气动力学模型图Fig.1 Aerodynamic model of the vocal cords
本文建立的声带的空气动力学模型如图1所示,声门入口半径Rin=0.15cm,出口半径Rout=0.108cm,声带轴向长度lg=0.308cm,声带宽度Lg=0.5cm,声门入口偏转角φin=50°,出口偏转角φout=90°,入口部分的轴向长度Lin=0.2cm,出口部分的轴向长度Lout=1.5cm.气流出口压力设为标准大气压,入口压力根据实验需求设置不同的数值.
流体在运动过程中遵循机械运动普遍适用的守恒定律: 质量守恒、动量守恒、能量守恒.由于本模型中气流雷诺数小于4000,可认为流体为均质、不可压缩.在忽略重力的情况下,声门内流场可由Navier-Stokes方程表示:
(2)
同时对于定常、不可压缩流体,密度ρ为常数,其质量守恒方程(连续性方程)表示为
(3)

其中:vx,vy,vz分别为x,y,z方向上的速度分量;ρ为空气密度;P为空气压力;μ为空气的黏性系数.
在求解气流控制方程时,将计算区域划分为一系列不重复的控制体积,并使每个网格点周围有1个控制体积,将待解的微分方程对每个控制体积积分,得到1组离散方程组.在对模型进行网格划分离散化后,利用SIMPLE(Semi-Implicit Method for Pressure Linked Equations)算法迭代求解压力-速度关联方程.首先给定单元面压力场的估算值,并使用此估算值求解动量方程得到该单元面的速度场,然后通过求解压力修正方程得到压力的修正值,基于压力修正值对压力场和速度场进行修正并检查结果是否收敛,若不收敛,则以修正后的压力作为新的估算值继续迭代计算,直至满足收敛条件.
1.3 发声阈值压力表达式的修正

(4)
式中:ρ=1.3×10-3g/cm3,为空气密度;v为平均速度,与体积流量U和横截面积A之间的关系为U=vA.
但是由于声门内黏性损失力的存在,实际的声带压力测量实验中Pin≠Pout[15].设声门入口处黏滞效应的损失系数为kloss,则肺部气压与声门入口之间的压力差为
(5)
式中:U是声门内气流的体积流量;lg是声带长度;d为声门直径;lg与d的乘积即为声门的横截面积A.
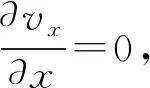
(6)
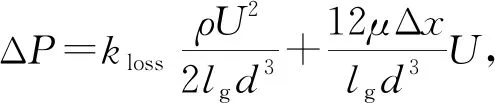
(7)
利用声带空气动力学模型对声门内流场进行数值求解,可以得到声带两侧受力和声门内气流的体积流量,同时设置不同的声门直径参数,并对其施加不同的声门下压,代入式(7)中,可得声门入口损失系数和声门直径之间的关系.对声带空气动力学模型中的d分别设置为0.005,0.0075,0.010,0.020,0.040,0.080和0.160cm,每种声门直径下均采用300,500,1000,1500Pa的声门下压作为声门入口的边界条件.图2(a)展示了不同声门下压时声门直径与入口损失系数的曲线关系.从图2(a)中可以看出,对于较低的声门下压,声门入口损失系数随着声门直径的减小有显著地增加,并且声门入口损失系数与预发声声门直径呈现出1种反比例函数的趋势,表明声门入口损失系数为非恒定数值.将入口损失系数与声门入口直径相乘,可以得到图2(b)的结果.对其中的曲线进行多项式拟合,得到声门入口损失系数与预发声声门直径之间的关系表达式,即
(8)
其中α,β,ε为由实验决定的常数.由于入口损失系数仅与声带形状相关[10],α值的选取取决于具体的声带模型尺寸.此外,对于式(7),设置不同的声门直径和声门下压,得出不同声门下压时入口损失系数和声门直径之间的曲线关系,在图2中,不同的声门下压得到的曲线关系基本是一致的,说明入口损失系数与声门直径之间的关系不取决于声门下压的改变.

图2 不同声门下压时入口损失系数和声门直径之间的关系Fig.2 The relationship between entrance loss coefficient and glottal diameter under different glottal pressures
将式(8)代入式(1)中,得到发声阈值表达式.在计算过程中,为了使参数达到最小,将其进行简化,令ε=0,最终修正后的阈值压力表达式为
(9)
通过这种形式可以直接确定发声阈值压力表达式的斜率和截距,将阈值压力表达式的斜率和截距与声带模型本身配置的参数建立联系,解决了预发声声门直径等于零时而阈值压力不为零的问题.
2 发声阈值压力表达式修正的实验验证
为了验证修正后发声阈值压力表达式的有效性,将求解出的发声阈值压力的表达式与前人的实验结果进行拟合.Chan等[9]搭建了在硅胶膜下植入生物力学材料的声带物理模型,通过在声带模型中加入不同浓度的透明质酸(HA)来改变声带黏度,以测得不同声门直径下的发声阈值压力.将修正后的发声阈值压力的表达式和Chan等的实验数据进行比较时,首先要确定入口损失参数α和β.Chan等的实验是基于半喉模型而非对称的M5模型,但声门具有较大宽度时半喉声带与对称声带的入口损失系数没有太大的区别,因此α值与Chan等的实验中的相同,考虑Chan等使用的实验装置尺寸,当α值为0.385cm时,可以较好地拟合出0.01%透明质酸(P-=12880g/s2)填充声带时的情况(其中声带宽度Lg=2.22cm,声带垂直厚度T=1.11cm,下质量块厚度d1=5T/6),同时为简化计算,将β值设为1,结果如图3所示,其中Eq.为式(9).
图4是在0.01%浓度的透明质酸中加入纤连蛋白(P-=17600g/s2),然后填充声带所得的实验结果.可以发现在相同的声门宽度下,纤连蛋白的填充会使声带发声的阈值压力增大,如图4中虚线所示.与式(9)保持一致,增大P-需要更大的截距和更陡的斜率.
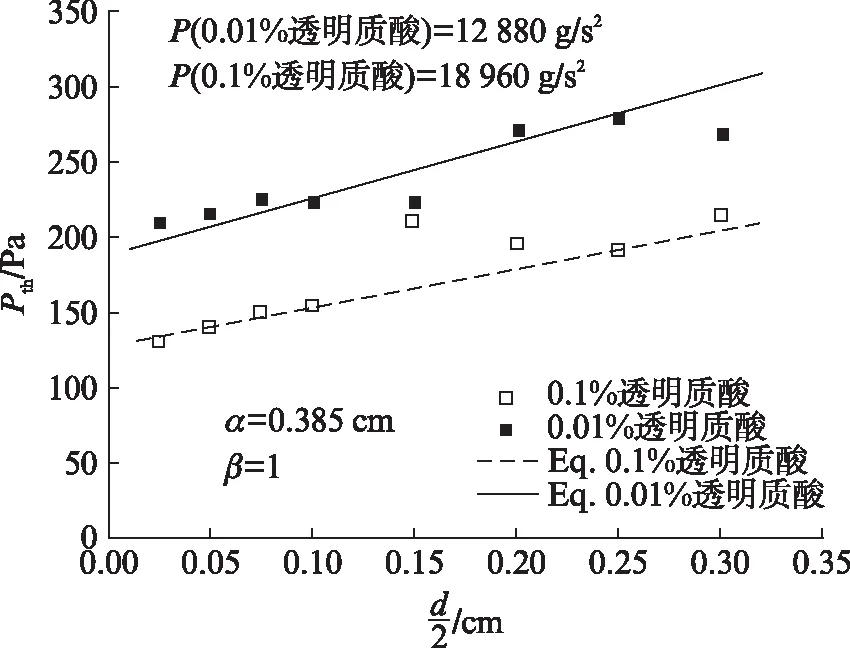
图3 2种浓度的透明质酸中发声阈值 压力与声门半径之间的关系Fig.3 The relationship between the phonation threshold pressure and glottal radius in two concentrations of hyaluronic acid
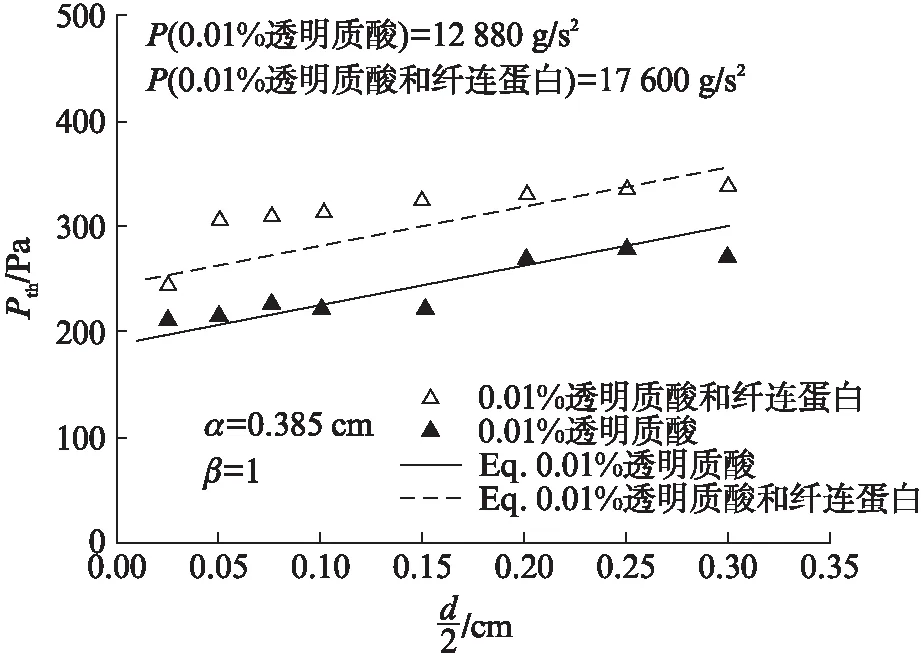
图4 加入纤连蛋白的0.01%浓度的透明质酸中发声 阈值压力与声门半径之间的关系Fig.4 The relationship between the phonation threshold pressure and glottal radius in 0.01% concentration of hyaluronic acid added to the fibronectio
表1是浓度为0.01%,0.1%的透明质酸和加入纤连蛋白的0.01%浓度的透明质酸中阈值压力的预测误差.表1中,在所有阈值压力的预测中,误差最小可以达到0.36%,最大不超过30%.上述实验结果可以验证修正后的阈值压力表达式能够较准确地预测声带发声时的阈值压力,同时能够解决当声门半径为零,发声阈值压力不为零的问题.

表1 声带模型中加入不同填充物时阈值压力计算值与 测量值的误差Tab.1 The error between the calculated value and the measured value of threshold pressure when dif- ferent fillings are added to the vocal cord model
3 结 语
为了对Titze提出的阈值压力表达式与其实验结果不相符的问题进行修正,本文从发声原理的角度建立声带的空气动力学模型,考虑声门入口损失系数与发声时的声门直径的关系,修正阈值压力的表达式,解决在声门直径较小时发声阈值压力不为零的问题.将修正后的阈值压力表达式与前人的实验结果进行对比,说明本文算法可以较准确地预测发声阈值压力的变化趋势,并且能够满足阈值压力在声门直径较小时不为零的情况,更符合实际上的嗓音的发声条件.本文主要考虑了声门半径与声门入口损失系数之间的变化关系,进一步的研究将考虑声带厚度、下质量厚度等相关因素对声门入口损失系数的影响.

