基于客观特征的民族乐器音色分析
江益靓,孙校珩,梁晓晶,李子晋,李 伟,3
(1. 复旦大学 计算机科学技术学院,上海 201023; 2. 中国音乐学院 音乐学系,北京 100101;3. 复旦大学 上海市智能信息处理重点实验室,上海 200433)
1 研究背景
不同旋律的音色可能具有不同的性格,从而表达不同的感情以及艺术风格.音色被定义为音高、响度相同条件下,能够区分不同声音的感知特征[1].而在动态的乐器演奏中,影响人们对于音色感知的因素是多方面的.基于音频特征,对音色的主观感知进行分析、建模,这对音色的感知研究和乐器的感知研究都有重要意义,是乐器识别、音乐情感分析、音乐流派分类等音乐信息检索任务的基础.
音色的感知描述较为主观,其研究需要大量的主观实验与对应乐器演奏的音频.研究大多采用多维尺度(Multidimensional Scaling, MDS)分析的方式,将乐器映射到低维空间中,进而分析乐器的音色[2].文献[3-5]研究了声学参数(起奏时间、谱质心、谱通量等)与MDS分析得到的乐器分布的关系.有关乐器感知实验的研究多针对合成或修改(变调)的声音为主[2-4,6],使用真实乐器的客观数据的研究较少,而实际上合成音色与真实音色有较大区别.相对于主观音色感知分析,基于客观特征的音色分析更加客观,可以更好地分析和理解音色本质,对于音色客观评价体系的建立有重要意义.文献[7]建立听觉感知模型,探究了同一乐器响度、音高与音色明亮度的关系.文献[8]分析了时域、频域、倒频域方面的音色特征.
民族乐器的音色感知方面的研究存在描述词选择较主观、音频数据乐器种类较单一、数据量较少的问题.文献[9]从音乐信息可视化的角度,研究了多种民族乐器的音色性格.文献[10]关注音色感知的单一方面,对中国民族乐器做了一系列主观评价实验.文献[11]建立了比较全面的民族乐器音色的主观评价数据集,并使用客观音色特征,对筛选出的16个音色描述词中的4个描述词进行回归建模.本文在文献[11]的民族乐器音色描述词的主观打分的基础上,进一步筛选出合适的描述词,然后基于客观特征,对4个音色进行分类分析.根据实验现象,本文基于客观特征进一步分析了音色的影响因素.
2 方 法
2.1 音色特征的选择
本文参考以往文献,从时域、频域以及倒谱域,选择与音色相关的特征[8,12].时域特征反映声音的动态变化.Helmholtz在1954年指出音色感知与频谱包络有关[12].在各类音色分析实验中,谱特征也是学者们研究的重点.本文采用谱质心、频谱峰态、频谱带宽、高阶谱拟合系数、频谱滚降系数、谱通量、协噪比作为频域特征.不同的谱特征表达声音不同的物理特征,其中: 谱质心主要体现了音色的明亮度;频谱滚降点表明了频谱包络开始快速下降的频率;谱通量为连续帧之间频谱的变化等.乐器发声的原理与人的发声类似,是激励和“滤波器”卷积的结果,而音色常被认为与滤波过程有较强的相关性,因此提取与人耳听觉特性相关的13维Mel频率倒谱系数(Mel Frequency Cepstrum Coefficient, MFCC)作为特征.实验中对每帧(50ms)提取上述特征值,取1段音频内的平均值作为该段音频的特征参数.
2.2 机器学习模型选择
在机器学习模型选择中,本文选择了下面几种算法.
1) 逻辑回归算法 建立代价函数,然后通过优化方法迭代求解出最优的模型参数.方法简单直观,适用于解决非线性问题.
2) 支持向量机(Support Vector Machine, SVM) 通过构造核函数,将原始数据映射到高维空间中,使得乐器演奏样本在该空间中线性可分.
3) K近邻算法 待分类样本是其临近样本的平均或投票结果,具有很强的容错性.
4) 随机森林 随机森林集成了多棵决策树,通过数据随机选取与特征集随机选取,进行分类,其最终分类结果为所有决策树投票的结果.
5) 梯度提升决策树(Gradient Boosting Decision Tree, GBDT) 在每轮迭代后,通过前项分布算法更新分类器权值.
6) Adaboost 在每轮训练结束后,Adaboost降低前1轮被正确分类的样本的权值,增加前1轮被错误分类的样本权值,对每个弱分类器的结果进行加权表决,提高误差小的弱分类器的权值.
本文使用网格搜索与五折交叉验证的方式选择机器学习模型的最佳参数.
3 实 验
3.1 数据集
3.1.1 数据集Ⅰ: 民族乐器音色主观评价数据集
本实验使用文献[11]中构建的民族乐器音色主观评价数据集.数据集包含37种民族乐器的样本数据,每种乐器包含1段3~4s的演奏片段以及1段音阶.采样率为44100Hz,采样位深为16bit.乐器按照类别可以分为拉弦乐器、簧管类吹奏乐器、边棱类吹奏乐器、弹拨乐器、打击乐器.文献[11]从调查问卷和文献中查找到329个音色描述词,通过一系列词语选择、相关性分析、聚类分析等步骤,得到16个乐器音色描述词,并让34位具有音乐专业背景的调查者听每种乐器的演奏片段,对听到的乐器音色在16个描述词上进行打分(1~9分).
3.1.2 数据集Ⅱ: 民族乐器扩充数据集
由于数据集Ⅰ中样本数据量较少,每种乐器仅有1段演奏片段,为研究民族乐器的音色特征,本文对其进行了扩充.首先,本文从视频网站上收集了37种民族乐器的独奏音频,进行去空白、归一化、剪裁等处理,获得了3933条长度为5s的样本数据.然后,本文在同种乐器的音频具有相似音色的假设前提下,认为搜集的音频与数据集Ⅰ中相应乐器演奏的音频具有同样的主观打分,并依据乐器种类对扩充的样本数据进行了标注,得到了带标签的扩充样本数据集.
3.2 实验一: 乐器描述词的选择
文献[11]挑选出可以完整描述出整个音色空间的16个描述词,分别为纤细、明亮、暗淡、尖锐、浑厚、单薄、厚实、清脆、干瘪、丰满、粗糙、纯净、嘶哑、协和、柔和、混浊.在此基础上,本实验依据37种乐器音频的主观音色打分,分析不同描述词之间的相似性,进一步简化音乐描述词.
3.2.1 多维尺度分析
首先,本实验对有效数据进行平均,计算出描述词之间的欧式距离矩阵.然后通过MDS分析将该距离矩阵转换成目标距离并进行降维,将16个描述词映射到低维空间中,使得低维空间中的距离最大程度地拟合目标距离.空间中描述词彼此之间的相对距离可反应描述词的差异程度.本实验采用应力系数作为拟合程度的衡量指标,即原始空间与构建空间距离差的平方和[13].应力系数越小,表明拟合的越好,见图1(a).
由实验可看出,维度为2时对应的应力系数为0.068,维度为3时对应的应力系数为0.046,达到“good”与“excellent”之间[13].维度更高时,应力系数的改变不大.此外,对应空间复杂度越高,计算量越大,综合空间的直观性,故选择3维空间对音色描述词进行MDS分析.MDS分析结果的可视化见图1(b).
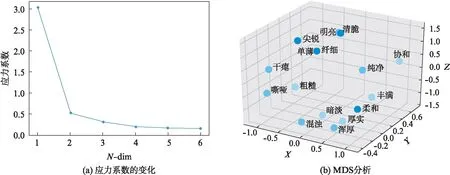
图1 应力系数的变化与MDS的分析结果Fig.1 The change of stress coefficient and the analysis results of MDS
从图1中可以看出,明亮、清脆以及纤细距离近,浑厚与厚实距离近,表示在感知上有较高的相似度.协和、纯净与粗糙、嘶哑距离远,清脆、明亮、纤细与浑厚、暗淡、厚实距离远,表示在感知上有较大的差异性.
3.2.2 聚类分析
由上节实验结果可知,部分词语距离非常接近,如明亮与纤细,浑厚与厚实,可以进一步简化.根据描述词在感知距离空间中的分布,可以将感知相近的词语聚类.本实验使用K-Means聚类算法,获得描述词在MDS3维空间中的聚类.K-Means是1种迭代求解的聚类分析算法,简化后描述词的个数就是聚类个数,与聚类中心最近的词语就是该类的中心描述词.本实验使用反映类间协方差与类内协方差的Calinski-Harabasz(CH)指标来选择聚类中心个数,该值越大表示类自身越紧密、类之间越分散,即聚类结果越好.图2(a)表示CH指标随聚类个数的变化情况.

图2 CH值的变化情况与聚类分析结果Fig.2 The change of CH value and the results of cluster analysis

表1 音色描述词的选择Tab.1 The choice of timbre descriptors
当聚类中心个数由3到4时,CH指标有1个跃升,之后略下降.当聚类个数超过8时,CH值逐渐增加,但聚类中心过多,没有起到简化的目的.因此,本实验最终选择4个聚类中心——即4组描述词来描述音频的音色.聚类的可视化效果见图2(b).本实验从聚类分析得到的每组音色描述词中,选择嘶哑、纤细、纯净、厚实这4个具有代表性且具有区分度的词语作为中心描述词,将16个音色描述词简化为4个,如表1所示.
经统计学方法验证,厚实与纤细负相关达到显著性水平(p<0.05).纯净与嘶哑在空间中距离较远,一定程度上也呈负相关.接下来,根据文献[11]中音色描述词的打分,将聚类描述词的分数取平均,得到中心描述词分数,并规定得分最高的描述词为该乐器的主导音色,结果见表2.
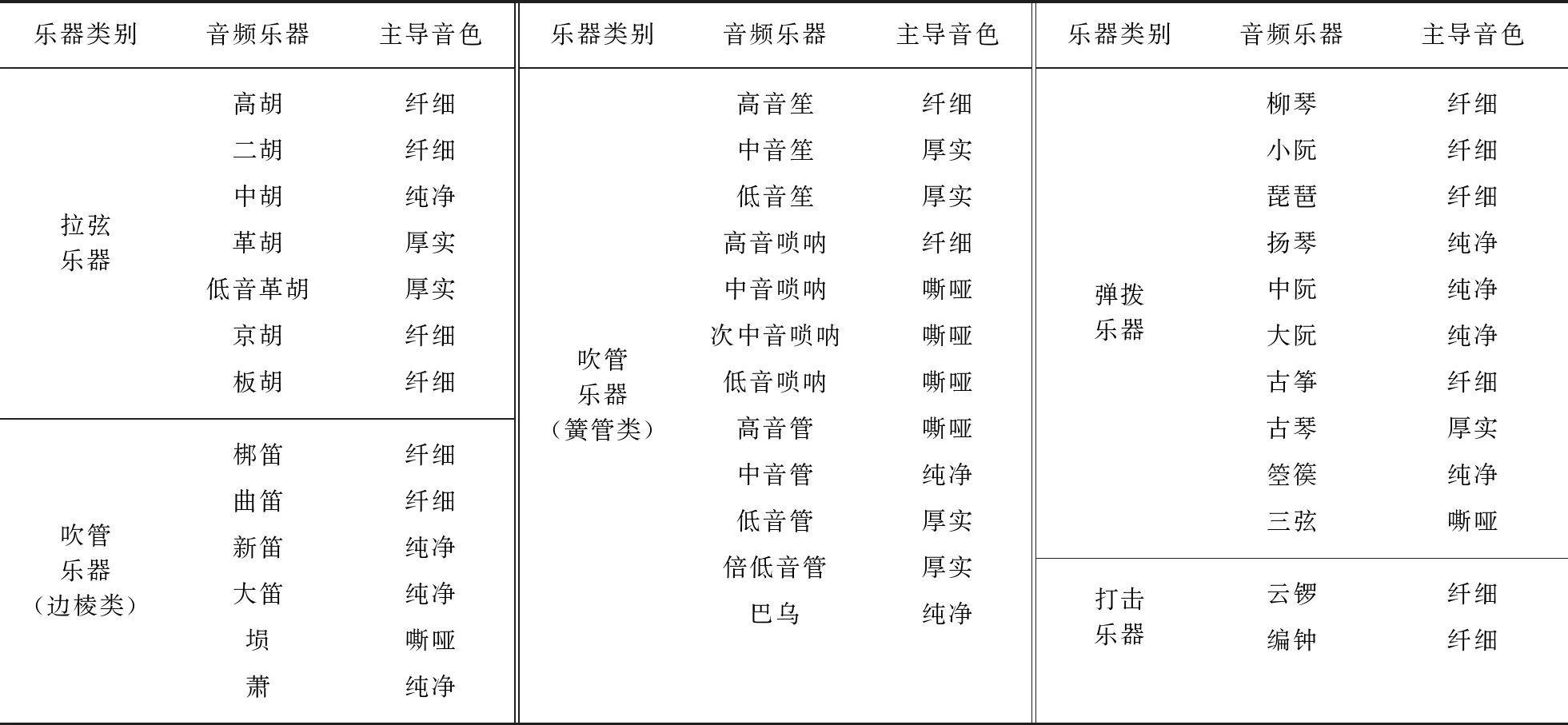
表2 民族乐器的主导音色Tab.2 Dominant timbre of Chinese musical instruments
3.3 实验二: 基于客观特征构建民族乐器的音色分类模型
本实验通过提取音频客观特征,使用机器学习方法建立民族乐器的音色分类模型.实验使用数据集Ⅱ(民族乐器扩充数据集)作为训练数据,乐器音色标签为表2所示的主导音色.首先使用网格搜索法选择各个分类器的最佳参数,再以音频片段为单位,使用五折交叉验证的方法计算出在验证集上的平均准确率.用具有准确主观打分的数据集Ⅰ(民族乐器音色主观评价数据集)作为测试集.每段音频以帧为单位提取21维音频客观特征,平均、标准化后送入分类器进行训练.实验结果如表3所示.

表3 民族乐器的音色分类模型的结果Tab.3 The results of timbre classification model of Chinese musical instruments
从表3中看出,经过参数调优后的几个模型中,带有径向基核函数的支持向量机分类模型表现最好,达到了78.38%的准确率与78.59%的F1值,计算出了较理想的分类超平面;逻辑回归结果准确率仅达到64.86%,表明音色与特征之间是非线性关系;同一乐器具有相同音色的假设会引入部分噪声,对噪声鲁棒性不强的随机森林表现稍差;而K近邻算法中,预测样本的音色为特征空间相近的样本标签投票的结果,具有较好的容错性.
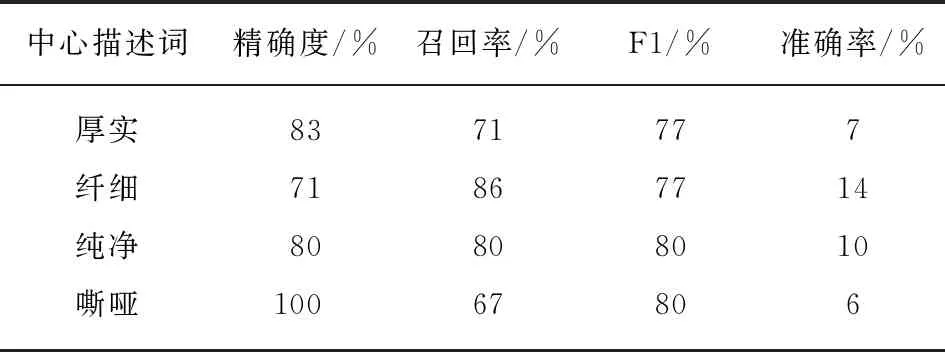
表4 SVM的分类结果Tab.4 Classification results of SVM
具体到音色,最优分类器(即SVM)的分类结果如表4所示.在训练数据中,标签为纤细的数据量较多,其中不同类型的乐器都出现了标签为纤细的样本,如数据集I中拉弦类乐器高胡、簧管类吹奏乐器高音笙、弹拨类乐器琵琶、打击类乐器编钟.然而事实上,由于乐器类别不同,这些乐器在整体音色感知上是有一定区别的,这导致纤细类别召回率最高,但精确度较低.其他3类精确度较高,但召回率较低.其中,嘶哑的精确度达到1.00,而召回率仅为0.67.音色类别为嘶哑的乐器多集中在簧管类吹奏乐器上,类型比较集中.另外,标签为嘶哑的数据量较少,且嘶哑聚类中的描述词间隔也较远,使用聚类中心词描述会引入一些偏差,使得召回率变低.具体到乐器类别,最优分类器(即SVM)的分类结果中,拉弦乐器的预测准确率达到85%,边棱类吹奏乐器准确率达到83.33%.
实验二表明: 基于客观特征构建民族乐器的音色分类模型有一定的分类效果,最好情况下达到了78.38%的准确率.由于实验基于同一乐器拥有相同音色的假设前提,使得标签中有一些噪声.训练出的模型会受到噪声的影响.针对以上分析的现象,本文从特征出发,对民族乐器音色进行进一步分析.
3.4 实验三: 基于客观特征的民族乐器的音色分析
在前面的分类实验中,分类器对不同的音色描述词进行建模时,表现差异较大.t-SNE(t-distributed Stochastic Neighbor Embedding)是1种用于挖掘高维数据的非线性降维算法,它非常适用于高维数据的可视化操作.为找到客观特征与音频音色之间的相关性,本实验将实验二中提取的音频片段的客观特征作为21维向量,通过t-SNE算法将其降维到2维空间,并对数据集Ⅱ中的3000多个音频片段在该特征空间中的位置进行可视化,观察标签为不同音色的样本数据在2维平面上的分布,对特征与音色之间的关系进行进一步分析.样本特征的可视化结果如图3所示.

图3 样本特征的可视化分析Fig.3 Visual analysis of sample features
首先可以看出,图3中相同标签(颜色)的音频有集聚现象.图中标签为纤细(黄色)的音频,有一部分明显远离其他标签的音频,另一部分零散地分布在中下部分,和纯净、嘶哑的分布较接近,加之数据量较多,出现了召回率高、精确率低的现象.标签为厚实(绿色)的音频,在图中分布较为集中,在K近邻算法中表现较好.图中标签为纯净(蓝色)的音频,整体居于平面中间靠右下的位置,但熵较大.图中标签为粗糙(红色)的音频分布最为分散,且与其他音频没有明显的分割边界.针对以上实验中观察到的现象,本文进一步分析了音色的影响因素.
3.4.1 音色与乐器类别相关性
同为弹拨类乐器,古琴、古筝与箜篌的主导音色标签分别为厚实、纤细与纯净.但在图4中,它们位置接近.这表明同一乐器类别的音频可能音色相近,例如拉弦类乐器多为纤细,簧管类吹奏乐器多为嘶哑、厚实,弹拨类乐器多为纤细、纯净.这与乐器的结构、材质、演奏方式有关.其中也有一些例外,如弹拨类乐器中,革胡与低音革胡声音厚实,这通常与乐器的演奏音域有关.

图4 同一乐器类别不同标签的音频分布Fig.4 The distribution of audio of the same instrument categorie with different labels
另外,由上述实验观察到,同一音色标签的乐器音频可能分布在特征空间上距离较远的位置.例如,在图5中,音色标签为嘶哑的乐器音频集中分布在空间的几个不同区域,而同一区域内大多是同一种乐器.如高音管在空间的右上方,埙在空间右部,三弦在空间左下部,其中高音管与标签为纤细的音频分布较近,埙与标签为厚重的音频分布较近,三弦与标签为纯净的音频分布较近.这表明即使同样是嘶哑,在主观感受上也并不完全相同,而是会受到乐器类别的影响.简单来讲,嘶哑可细分为簧管类吹奏乐器的嘶哑(高音管)、边棱类吹奏乐器的嘶哑(埙)、弹拨类乐器的嘶哑(三弦)等不同种类.

图5 不同乐器类别同一标签的音频分布Fig.5 The distribution of audio of the different instruments categories with same label
其他音色描述词也有类似结论.如拉弦类乐器的厚实(革胡)、弹拨类乐器的厚实(古琴)、吹奏类乐器的厚实(低音管)在特征分布空间上也有类间距离较远、类内距离较近的现象.综上所述,乐器音色与乐器类别有关.同一类别乐器的音色感知相近,不同类别乐器的音色感知差异较大.
3.4.2 音色的其他影响因素
通过实验可以发现,相同乐器的不同音频片段被模型预测为不同音色的情况普遍存在,这是因为音频的音色不止取决于演奏的乐器种类,还受到音频其他性质的影响,如音高等.
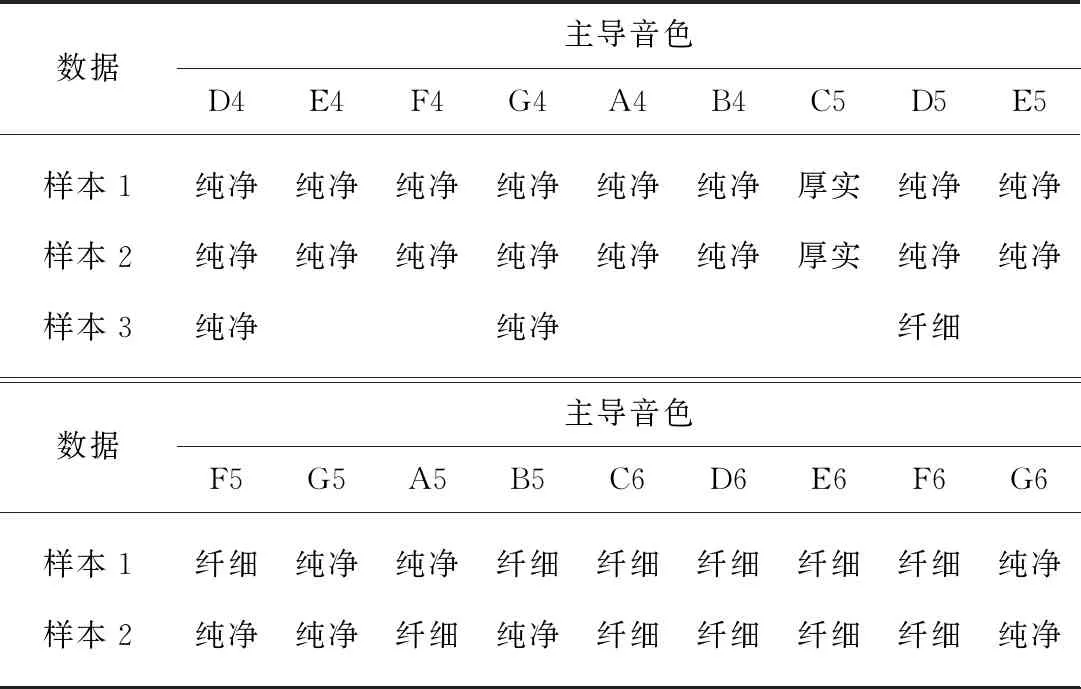
表5 不同音高的音频的预测结果Tab.5 The prediction results for audio samples with different pitches
新笛乐器在各个描述词上的主观打分较均匀,本实验选取新笛的音频进行实验.首先将按音阶演奏的新笛音频片段按照音高进行分割,使得每段音频音高基本稳定,得到反映18个不同音高的39个样本数据.然后使用实验二中得到的分类器对样本数据的主导音色进行预测,预测结果如表5所示.
由表5可知,新笛音色在“纯净”上得分最高,但是从上述实验结果可以发现,随着音高升高,音频逐渐趋向于被预测为“纤细”.同样地,本实验使用了t-SNE算法对包含这39个音频的样本数据集的特征进行了可视化,并将39个音频的音高标记在空间中,见图6.

图6 同一乐器不同音高的音频分布Fig.6 The distribution of audio of the same instrument with different pitches
可以发现,新笛的音频片段在空间中的分布并不集中,而是以一定的规律分散在空间的不同位置.具体而言,音高高于B5的音频主要分布在标签为纤细的点(黄色点)附近,而音高低于B5的点则主要分布在标签为纯净的点(蓝色点)附近,与分类器的预测结果相一致.由此可知,对于1段音频仅凭其演奏乐器难以断定其音色,换言之,同一乐器所具有的音色属性并不单一.因此,通过演奏乐器映射到单一音色的样本数据集具有一定局限性,使用其所训练的分类器同样较为局限.此外,通过本实验也可以发现,实验二中训练的分类模型预测结果与主观认知基本一致,证明了模型的有效性.
4 总结与展望
本文基于客观特征对民族乐器音色进行了研究与分析.首先,本文通过音色描述词的主观打分,进行了描述词的分析与聚类选择,将16个音色描述词进一步分为具有区分度的4个音色类别——厚实、纤细、纯净、嘶哑.基于同种类乐器具有相似音色的前提,本文构建了民族乐器的音色分类模型,其中支持向量机模型表现最好(精确度为83.48%,召回率为75.95%,F1值为78.59%,准确率为78.38%).根据实验中观察到的现象,本文进一步分析了音色的影响因素,发现除与乐器种类有关以外,音色还与乐器类别相关,同一类别乐器的音色大体相近,不同类别乐器即使用同一音色描述词描述,音色仍可能有较大差异;除此之外,音色还受多重因素影响(如音高),同种类乐器仍可能具有多种音色属性.
前文的研究证明,单一的主导音色也许不能完全代表乐器的音色感知特征,对研究过程中发现的诸多局限性,未来的研究可关注下面几个方面: 1) 尝试多标签分类或建立连续的音色空间模型来更精准地对音色建模;2) 影响音色的其他因素,如演奏技法、演奏力度等;3) 由于从互联网收集的独奏片段录音环境、录音设备及后期处理并不统一,可尝试建立条件统一、质量更高的民族乐器的音色数据集.

