任务期间多层级不完全修复件的备件配置优化

刘任洋，杨瑞平，赵 冰，于风竺

（海军研究院，北京 100161）

0 引言

可修复备件是指故障后可以修复的备件类型。这类备件资源往往价格昂贵、具有较高的故障率。有关资料显示［1］，在多层级设备所有部件中，20 %的可修贵重器材占据了80%的备件保障费用。因此，对可修复备件资源进行科学合理的配置和规划是当前维修保障工作中的重点问题。

根据保障周期内是否存在订购和补给，备件保障模式可以分为自主保障和多级保障。多级保障是较为常用的对设备实施多级维修供应的保障模式，保障周期一般较长，其库存建模方法主要基于稳态的Vari-METRIC［2］模型和动态的Dyna-METRIC［3］模型（以下统称“METRIC 理论”）。与多级保障相比，自主保障无外部供应和补给，仅依靠自身的备件资源和维修条件实现自我保障。当任务持续时间短、强度较低、任务区域离后方保障基地较近时，通常实施自主保障。目前在自主保障下对可修复备件库存建模的研究大多基于马尔科夫过程理论。文献［4-5］把可修件库存模型看作M/M/c 排队系统，利用排队论方法求解系统稳态时的备件满足率。文献［6］根据“累积失效概率相等”原则将非指数型部件等效为指数部件，从而对其库存状态利用马尔科夫过程建模得到备件保障概率。

然而，无论是METRIC 理论还是马尔科夫过程理论，均以经典的库存平衡方程［1］为基础，即当前库存量与初始库存量、在修数量以及备件短缺量存在一种动态平衡。这就要求在整个保障体系内，故障件必须完全可修［7-10］或当修复不了而报废时则必须从外部获得补给［11］以维持库存平衡，否则库存平衡方程一旦打破，上述理论都不再适用。而设备在实际执行任务期间，受保障条件限制可能只得到部分保障组织的支持甚至仅实行自主保障，绝大多数备件满足不了完全可修的条件，属于不完全修复件，此时若不考虑外部的采购（从外部供应商的采购周期通常很长，不适合短期任务），如何在任务期内制定合理的备件方案以满足保障要求具有现实意义。

本文针对上述问题，在自主保障模式下结合任务期间备件报废的问题，利用近似等效思想提出了一种简单有效的备件优化方法，该方法旨在用简单巧妙的方式解决复杂的多层级库存建模问题，便于工程应用，为任务期间备件方案的评估和优化提供了新思路。

1 多层级不完全修复件的可用度评估

1.1 多层级部件不可拆卸不可维修单元处理方法

为了便于描述，以两层级部件为例。设某现场可更换单元（Line Replacable Unit，LRU）由N 个可拆卸维修的车间更换单元（Shop Replacable Unit，SRU）和若干不可拆卸不可维修单元组成，各单元寿命均服从指数分布，其中LRU 和SRUi（i=1，2，…，N）的平均寿命分别为MTBF0和MTBFi。LRU 的故障由其所属的任一单元（包括SRU 和不可拆卸不可维修单元）故障所致。LRU 的维修只能通过更换故障SRUi完成，SRUi为不完全修复件，仅以一定概率修复成功。当LRU 故障原因是由不可拆卸不可维修单元引起时，该故障LRU 则会因无法维修而报废。不考虑重测完好率、虚警率等维修参数的影响，把所有不可拆卸不可维修单元当作一个整体单元，设其平均寿命为MTBFleft，则有：

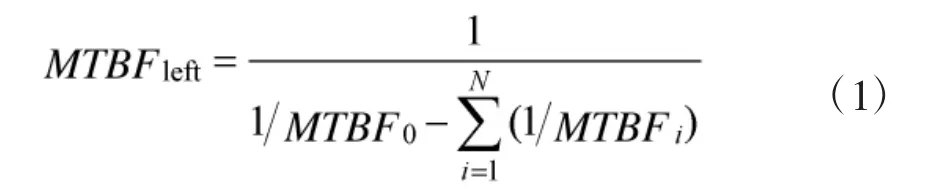
以上处理方法实现了由部件层次结构到备件层次结构的转变，反之，在仅已知备件层次清单时应考虑某些在部件层次结构中存在，而在备件清单中没有出现的部件或单元，将其统一看作隐藏在设备相应层级的一个整体，该整体为不可拆卸不可维修单元，平均寿命由式（1）得到。需要说明的是，不可拆卸不可维修单元虽不存在备件配备问题，但其影响上层部件故障的发生以及报废，因此，在设备备件模型搭建中须将其考虑在内。

1.2 不完全修复件的消耗件等效方法

通过上述寿命等效过程，具有维修概率ri，平均寿命为MTBFi的不完全修复件被近似等效为平均寿命为MTBFei的消耗件。此时的LRU 由N 个SRUi消耗件和一个不可拆卸不可维修单元构成，其等效平均寿命MTBFe0为：

1.3 多层级备件数量的单层级等效

由于SRUi的备件完全用于维修故障LRU 并产生新的LRU 备件，因此，若能提前算出所有SRUi备件所能维修的故障LRU 总量，就能将该故障LRU总量作为LRU 备件去代替所有SRUi备件，从而将多层级备件问题转换为只需考虑顶层LRU 的单部件问题。

当LRU 发生故障，原因是其所属的某个SRUi故障所致的条件概率为：

设LRU、SRUi的备件配置量分别为S0、Si，则对故障LRU 维修一次所消耗的各SRUi的备件数量为：

将SRUi的备件消耗量等效折算为LRU 的备件增加量，即：

下面给出等效顶层LRU 备件数量Se0的计算流程：

Step 1：置累积LRU 备件增加量ΔS'0=0，初始可用LRU 数量Sav=S0+1（Sav包括备件数量和部件本身）；

1.4 可用度评估

满足任务要求的备件保障度量指标有多种，如备件保障概率（备件满足率）［12］、备件利用率［13］、设备可用度［14］、任务成功率等。本文选取常用的设备可用度指标进行建模。由1.3 节方法计算得到的顶层LRU 等效备件数量Se0通常为非整数，直接利用指数型备件保障概率公式将面临备件数量的近似取整问题，从而会导致一定的误差。而指数分布是伽马分布的特例，利用这一性质，可将指数型部件转化为伽马型部件处理。伽马分布的寿命分布函数为［15］：

一般假设设备各LRU 组件为串联的可靠性关系，则设备的可靠度为各LRU 可靠度之积：

任务时间T 内，设备可用度为期望工作时间与任务时间之比：

Fs（t）为设备的寿命分布函数，E 为期望工作时间。

2 备件优化模型及求解方法

备件的库存优化问题可描述为以规定的设备可用度为约束指标，寻求备件总购置费用的最低化，即：

A0为规定的可用度指标，ci为备件i 的单价。边际分析法是求解上述模型的常用方法，但由于本文近似方法未考虑维修延误，这在一定程度上弱化了顶层LRU 备件的效益权重，采用传统边际算法中逐个增添单项备件比较效益值的方法将导致顶层LRU 的配备数量极少，从而得到错误的备件优化方案。本文采用一种改进的边际算法，通过该方法得到的费效曲线可使相邻两个备件迭代方案各项备件数量均发生变化，而非传统边际算法中后一备件方案仅在前备件方案基础上增配某一项备件而来。具体步骤如下：

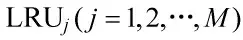
Step 2：令LRUj及其所属部件的备件数量分别从0 取至Xj，通过遍历方式产生各LRUj的初步备选方案，并计算每个方案的等效顶层备件数量和对应费用；

Step 3：将各LRUj中备选方案的等效顶层备件数量按从小到大排序，对应的备件方案和费用亦随之重新排序，并寻找等效顶层备件数量相差0.001以内的备件方案，保留其中费用最低者，其他方案剔除，得到经过初步筛选的各LRUj备选方案；

Step 4：采用以下方式对各LRUj备选方案进一步筛选：如果某一方案对应的备件费用比后面所有方案费用都低，则该方案保留，否则剔除；由此得到各LRUj的最终备选方案，这些备选方案随着各自等效顶层备件数量的增加，对应费用呈递增趋势；

Step 5：利用式（8）计算LRUj各备选方案对应的可靠度值，得到可靠度向量Rj，Rj中的各元素为LRUj对应备选方案的可靠度值。与前一备选方案相比，定义LRUj采用第个备选方案使设备可靠度的增加量与总备件费用增加量的比值为该LRU 第k 个备选方案的边际效益值，定义边际效益值与前一备选方案下设备可靠度的比值为相对边际效益值，根据定义有：

3 算例分析

设某船舶设备备件层次结构如图1 所示，在执行一个持续工作时间为2 000 h 的水域监测任务中，为了保证任务的顺利完成，规定该设备可用度须达到0.97，现要求制定相应的备件携行方案。备件的相关可靠性、维修性等参数如表1 所示。

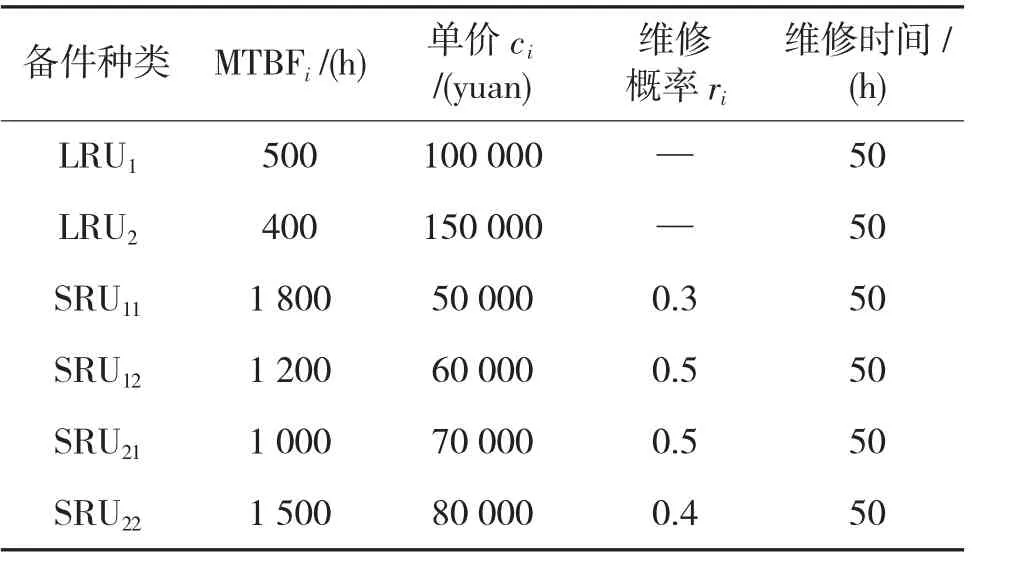
表1 备件输入参数

采用本文改进的边际算法，总共历经31 次迭代（LRU1历经15 次，LRU2历经16 次）得到最优备件配置方案如表2 所示，迭代的费效曲线如图2 所示。在该方案下的设备可用度为0.970 8，总费用为118 万元。

表2 备件优化方案

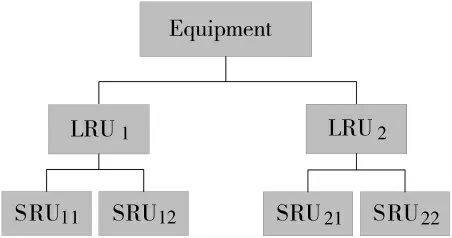
图1 设备层次结构

图2 费效迭代曲线

为了验证本文优化方法的正确性，采用Matlab平台构造仿真模型对所得最优备件方案进行评估。仿真模型主要包括备件需求发生模块、故障件维修模块、备件更换模块以及变量统计模块。仿真次数设为1 000，统计每次仿真的累计停机时间Td，（1-Td/T）即为可用度，取1 000 次仿真的可用度均值作为最终输出结果。将表2 所示的备件方案输入仿真模型，得到的设备可用度输出结果为0.952 8，本文近似方法的评估误差为1.89%，在可接受的范围内。将任务时间从1 000 h 取至10 000 h，得到近似方法和仿真方法的评估结果如图3 所示，图中两条评估曲线偏离不大，平均误差较小，为2.17%。尽管近似方法忽略了维修时间，但50 h 的维修时间相对于部件平均寿命而言并不长，从而降低了产生维修延误的风险，即便当维修延误发生了，较短的延误时间对可用度的影响却不大，因此，保证了近似方法的精度。

图3 不同任务时间下近似方法和仿真方法结果对比

为了进一步说明维修时间对近似方法评估效果的影响，令各部件的维修时间分别增加至200 h和400 h，得到图4 所示的可用度变化曲线。综合对比图3 和图4 可以看出，随着维修时间的增加，近似结果不变，而仿真结果不断偏离近似结果，近似方法的平均误差不断加大，由2.17 %分别增加至2.70%和3.91%。误差变大的原因是由于维修时间的大幅增加使发生维修延误的风险加大，并导致较长延误时间的产生，从而影响了近似方法对可用度的评估效果。通过大量试验表明，只要维修时间不是过大（将维修时间接近或大于对应LRU 的平均寿命视为过大），评估误差一般在可接受的范围内，本文优化算法所得的备件方案合理可行，基本能满足保障要求。

图4 不同维修时间下近似方法和仿真方法结果对比

4 结论

本文从任务期间设备的备件优化问题入手，结合任务期内普遍存在的故障件报废情况，利用近似等效思想提出了备件方案的评估和优化方法，并通过仿真方法与之对比验证，结果表明：只要维修时间不是过大，考虑维修时间与否对可用度的影响不大，本文优化方法得到的备件方案合理可行。需要说明的是，仿真方法虽然精度更高，但在实际处理大批量备件运算时，其时间将不可估量，不便于工程应用，这也是本文解析方法的优势所在。