巧用数形结合思想 提升学生说理能力

摘 要：数学是一门逻辑与思维、知识与方法并重的学科，数学语言是数学知识的重要组成部分，它不仅仅反映学生掌握知识的具体情况，也是学生展示学习方法、表达逻辑思维的交流工具。小学数学课堂教学中，如何运用数形结合思想，将抽象问题形象化，疑难问题简易化，让学生更容易、更有效地整合获取的信息，用精练、准确的数学语言有序地表达自己的观点，提升学生的说理能力，是值得老师深入探讨的话题。

关键词：小学数学;说理教学;数形结合

一、 引言

小学数学课堂教学中，说理教学对学生逻辑思维能力培养尤为重要，数形结合思想的应用，有利于促进说理教学改革，将数与量之间的关系论述转变为图与数的关系，便于学生学习数学知识，借助图形理解数学公式的内涵和分析数学问题。因此，小学数学教师在课堂说理教学中，应渗透数形结合思想，通过数与形的紧密结合，将抽象的数学知识形象化、生动化、鲜活化和趣味化，激发学生的数学学习兴趣，引导学生更深入思考，提升逻辑思维能力和表达能力。当然，这需要小学数学教师转变教学观念，积极创新与探索，寻求有效的数形结合思想的实施路径。

二、 数形结合思想在小学数学课堂说理教学中的重要性

在小学数学课堂说理教学中运用数形结合思想，有利于引导学生进行“有序”“有理”“有据”地进行说理。

（一）运用“数形结合”，让学生说得“有序”

我国著名数学家华罗庚先生曾经说过：“数缺形时少直观，形少数时难入微，数形结合百般好，隔离分家万事休。”数形结合作为一种非常重要的数学思想方法，在小学数学的教学中占有非常重要的地位，借助数形结合，能够引导学生有序地进行

“审题—分析—解题—总结”把“符号语言”转化成“图形语言”，通过对“图形语言”的深入分析，再转化成口头语言，有序的表达出来。

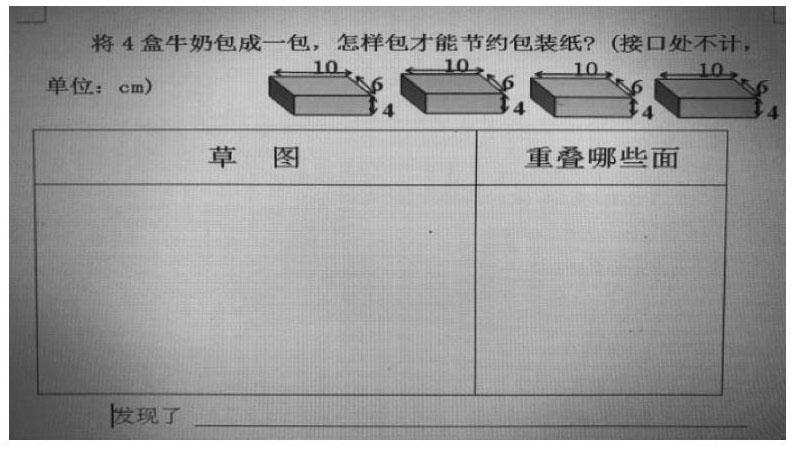
比如，在教学北师大版五年级数学下册——《包装的学问》一课例题2：将4盒牛奶包成一包，怎样包才能节约包装纸？那如何让学生能有序又不遗落的把这些方法说出来呢？执教者想到了数形结合，设计这么一份运用“数形结合”来解决这个问题，并让学生完成后进行交流。

这样，学生在分析题目的意思后，把自己的多种想法通过画一画表示出来，有利于在和同学交流中把自己有序的思考过程表达出来，做到不重复，不遗落，很快得出了8种不同的包装方法，其中，重叠6个面的有4种，重叠8个面的也有4种。

（二）运用“数形结合”，让学生说得“有理”

数学学科学什么？学“理”。只有让学生真正弄清算理，知道知识的来龙去脉，懂得数学知识之间的内在联系，才能让学生真正学会数学，学懂数学。从而更好地运用数学知识解决生活问题。那么，学生怎么才能讲清“理”？“数”与“形”作为小学数学教学的重点知识，“数”与“形”之间的转换，在这里起到了至关重要的作用。第一，数形结合思想的渗透，能把抽象的数学概念直观化，帮助学生形成概念，深化对数学概念等抽象知识的理解。第二，在说理教学中运用数形结合教学方法，能将文字信息转变为图形、把复杂的问题简化，学生在问题探究和分析中，能更好地整合现有信息，并理清数与量之间的关系，理解算法的同时学会运用算法。

比如学生在学习3的倍数的特征，让学生交流时，大部分学生受2和5倍数特征的负迁移，说出了“个位是3、6、9的数”能被3整除，有学生通过预习书本知识，知道了“各个数位上的数字之和是3的倍数，这个数就是3的倍数”，可是为什么？学生说不清这个“理”。有位执教者用面积模型引导学生进行说理：225能被3整除吗？

用面积图形分别表示出2个百、2个十和5。每1个百最多99个小正方形刚好是3的倍数，2个百就余2个，每个十最多9个小正方形也是3的倍数，又剩下2个，还有个位的5个，这样剩下的就是“2+2+5”，如果这些剩下的个数加起来，又是3的倍数，那么这些方格的总个数就是3的倍数。接着，执教者又让同桌互相举例，画图，说理，学生很快就把利用“数形结合的”例子把为什么“各个数位上的数字之和是3的倍数”说得非常有理。

（三）运用“数形结合”，让学生说得“有据”

所谓据，是依据和根据，让学生说得有据，学生就要快速运用自身所学知识，为自己的观念找好论据。对于小学生而言，论据为何，他们还不了解。想要让学生说得有据，更多的还是要从思维入手，激活学生的思维，深入引导学生了解知识的本质，参与问题探究中，深化对知识的理解，学生才能在脑海中理清知识之间的关系，并在问题探究中快速明确解题方向。运用数形结合开展小学数学说理教学，教师既要在教学设计中，根据数学教学的目标、重难点等，巧用数形结合的教学方法，加深学生对数学知识的记忆和理解;又要从已有的知识入手，针对学生的空间想象能力、逻辑思维能力以及运算能力培养，让学生联系日常生活经验，简化数学符号、公式等之间的关系，促使学生在学习中能归纳和整理好所学知识，这样才能深化对知识的理解，从而在问题探究和数学表达中有理有据。

三、 如何在小学数学课堂说理教学中渗透数形结合思想

小学数学课堂说理教学，本质上是要让学生理解数与量、数与形之间的逻辑关系，多数情况下教师会通过理论分析、举例分析等方式，深化学生对课堂数学知识的理解。然而，小学生认知水平不高，接受能力有限，说理教学所取得的效果并不显著。数形结合思想的渗透，则是为了改变这种现状，运用生动形象的图形，帮助学生理解数学概念、数学公式等，并将抽象的数与量之间的关系，转变为图形分析和文字信息转换，从而提升小学生的数学学习效果。

（一）提供充足时间，让学生“有空说”

数形结合思想的渗透，先要确保学生处于课堂的主体地位，把课堂时间真正还给学生，让学生有充分的时间，熟虑后，交流。小学数学所教授的知识，多数都是数量关系和空间平面图形互相转换等，说理教学中运用数形结合思想，也贴合教学内容。一方面，小学数学教师要在课堂教学中，借助多媒体设备展现生动形象的图形、反复使用数形结合思想，引导学生分析问题、解决问题。当学生领悟数形结合思想，就能更加主动地参与到问題探究中，融会贯通，在联系中也能更好地举一反三。另一方面，教师要基于学生个体之间的差异性，灵活地应用数形结合思想启发学生思维。毕竟学生的思维方式各不相同，学习效果也存在差异，有些学生在问题解决中，会习惯将形化为数来解决问题，有些则是趋向于直接用数量关系来解决数学问题。因此，在课堂说理教学中应用数形结合思想，教师应针对学生个体差异，实施差异化的教学方法，帮助学生寻找符合自身特色的解题思路。

（二）整合丰富的资源，让学生“有话说”

小学数学教学中，为了更好地运用数形结合思想，教师要先挖掘教材中与数形结合思想有关的知识点，采用数形结合思想灵活地设计教学环节。可以为学生课前准备一些操作的学具，或者可以设计学习单，通过画一画，摆一摆，涂一涂等，让学生运用“数与形”的有机结合，深化对这些知识的理解和记忆。尤其是概念性的知识，若是直接进行说理教学，学生往往都是一头雾水，要么是一知半解，很难在实际问题解决中借助概念进行信息分析。小学数学教师应在实际教学中，深入挖掘教材中的知识点，针对抽象的数量关系设计教学活动，引导学生将抽象、复杂的数量关系转变为图形解析。例如计算2/5×1/3=？教师可以让学生在图中涂出2/5×1/3，这样一来就将复杂的计算问题，转变为简单的图形解析，借助图形让学生理解分数乘法的算理，学生就能“知其然”，又“知其所以然”，运用计算公式时也能更加得心应手。这就让数学教学实现了從“授人以鱼”到“悟其渔识”的转变。

（三）创建趣味性的教学情境，让学生“乐意说”

趣味性的教学情境，便于学生感悟数形结合思想，活跃课堂气氛。例如在分数应用题教学中，教师可以用蜡烛创设问题情境，有一个长度为8cm和一个长度为6cm的蜡烛，两根蜡烛都烧掉同样长度后，发现原为6cm的蜡烛剩下的长度是原为8cm的蜡烛剩下长度的3/5，请问蜡烛燃烧了多少厘米？这样的问题情境，多数情况下学生都会设未知数，基于题目的意思进行列式计算。教师可以在这个时候，绘制烧掉部分的线段长度的图形，如下图所示：先让学生自己求解，再让学生依据图形进行计算，通过两次计算的过程和体验，学生能深刻感受到数形结合运用于解题是非常好的方法。长短蜡烛剩下长度的长度比为5∶3，即长蜡烛要比短蜡烛多2份，2÷2=1每份长度为1厘米，所以长蜡烛还剩5厘米，短蜡烛还剩3厘米，由此可得，长短蜡烛燃掉了3厘米。这样的分析过程，比起设未知数，更便于学生理清数与量之间的关系。

四、 结语

综上所述，小学数学课堂说理教学中，渗透数形结合思想，旨在深化学生对小学数学抽象概念、公式等知识点的理解，便于学生将抽象的数与量之间的关系转变为数与形，通过图形解析整理现有的信息，寻求解题方法。数形结合思想的渗透，也能进一步促进学生思维能力和观察能力的培养，真正实现以学生为中心，促进学生主动学习、思考、质疑、析疑，从而使小学数学教学改革落到实处。

参考文献：

[1]岳桂平.小学数学教学中数形结合思想的渗透研究[J].中华少年，2017.

[2]王美珍.关于小学数学课堂教学中数形结合思想的实施策略[J].新课程，2017（6）.

[3]石丽丽.数形结合思想在小学数学教学中的实践运用[J].新课程：小学，2015（3）.

[4]孙似男.小学数学课堂教学中渗透数形结合思想的研究[J].考试周刊，2014（91）：77.

[5]金荣.数形结合思想在初中数学课堂教学中的运用策略[J].新教育时代电子杂志：学生版，2016（26）.

[6]梁雪梅.小学数学课堂应用数形结合思想的教学方式解读[J].科教导刊，2017（10）：139-140.

作者简介：陈玲玲，福建省南安市，福建省南安市第一实验小学。